基于投影寻踪原理的机组可靠性等级评价

付忠广，景 源，齐敏芳，王建星

（华北电力大学 电站设备状态监测与控制教育部重点实验室，北京102206）

随着电力体制的改革，电厂实行了商业化运行并且竞价上网，这使得发电厂在保证安全运行的同时，越来越重视其经济性.因此，机组设备能否连续可靠运行变得尤为重要，它关系到企业的生产成本和经济效益［1］.提高设备的可靠性，可以增加其在市场中的竞争力.

机组可靠性等级评价是火力发电厂的现代管理方法，能够掌握机组运行情况，避免因机组事故强迫停运而造成经济损失［2］.因设备可靠性评估的影响因素很多，属于多维数据的研究范畴，国内现有的评价手段大多通过理论分析之后人为决定权重［3-4］，从而确定机组的可靠等级，客观性较差.鉴于投影寻踪方法具有能排除与数据结构、特征无关或关系很小的变量干扰的优点，可实现多指标样本分类等非线性问题且不依赖人为决定因素，因此，笔者以投影寻踪原理为基础，并结合遗传算法优化建立模型，实现了机组的可靠性等级评价，为设备的可靠性状态评估提供一条新途径.

1 投影寻踪简介

投影寻踪是由美国科学家Kruskal提出的一种用来分析和处理高维观测数据，尤其是非线性、非正态高维数据的新兴统计方法［5］，是统计学、应用数学和计算机技术的交叉学科，属当今前沿领域，具有稳健性好、抗干扰性强、准确度高等特点.它通过把高维数据投影到低维子空间，寻找能反映原高维数据结构或特征的投影，从而达到研究分析高维数据的目的.

投影寻踪方法的实质是构造一个量化的投影指标函数Q（a），通过使用数值方法优化，寻找出最佳的投影方向a，将多指标的数据转化为一维投影值z，从而对高维数据进行投影降维来实现所求问题的分析.具体步骤如下：

（1）样本集的归一化处理.

设各指标值的样本集为｛x＊（i，j）｜i＝1，2，…，n；j＝1，2，…，p｝，其中x＊（i，j）为第i个样本的第j个指标值，n、p分别为样本的个数（样本容量）和指标的数目.为消除各指标值的量纲和统一各指标值的变化范围，可采用下式进行极值归一化处理.

对于越大越优的指标：

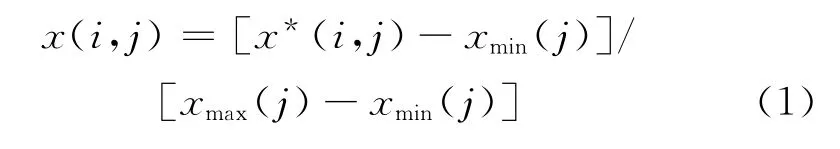
对于越小越优的指标：

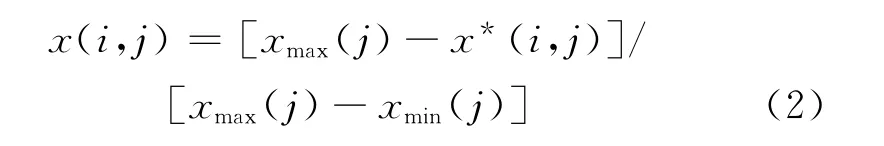
式中：xmax（j）、xmin（j）分别为第j个指标值的最大值和最小值；x（i，j）为指标特征值归一化后的序列.

（2）构造投影方向a.

构造p维单位向量a＝｛a1，a2，…，ap｝，使样本数据综合成以a为投影方向的一维投影值z（i），即

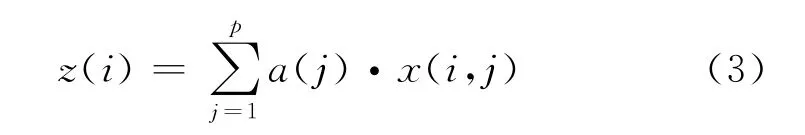
其中，i＝1，2，…，n.

（3）构造投影指标函数Q（a）.

针对所求的具体问题，对高维数据构造投影指标函数Q（a）.

（4）优化投影指标函数Q（a）以得出最佳投影方向a＊.

不同的投影方向反映了不同的数据结构特征，最佳的投影方向就是最大可能暴露高维数据某类特征结构的投影方向，因此，通过求解投影指标函数最大化问题来估计出最佳的投影方向a＊，即：Max：Q（a），约束条件：

（5）投影值分析.

将所求得的最佳投影方向a＊代入式（3）后得到各样本点的投影值z＊（i），对z＊（i）进行分析，发掘高维样本数据结构特征.

2 基于投影寻踪的机组可靠性等级评价

2.1 选取投影寻踪等级评价模型的样本指标集

全国各火电机组的可靠性水平不尽相同，为不失普遍性和科学性，构建等级评价模型所用的样本集取自《2010年全国火电600 MW 级机组竞赛运行数据汇总表》［6］（以下简称《汇总表》）中各集团公司超临界机组的运行数据，共16个机组，即样本容量n＝16.

一般机电产品的可靠性评价主要取决于设备的平均无故障工作时间或失效率［7］，对于大型火电机组，衡量可靠性的主要因素为：等效可用系数C1、非计划停运次数C2、等效强迫停运率C3和运行暴露率C4，其计算公式如下［8-9］.

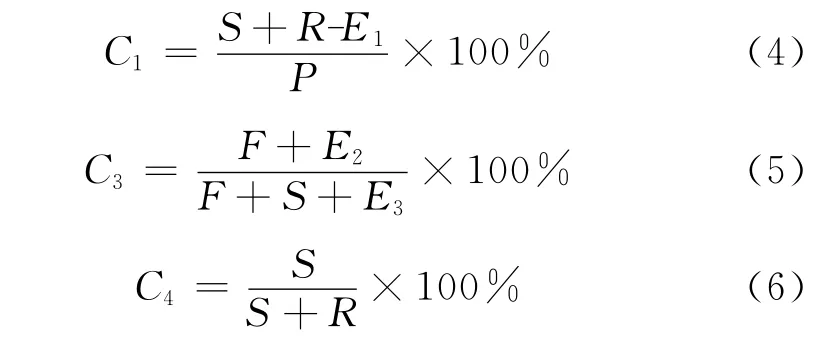
式中：S为运行小时数；R为备用小时数；E1为降出力等效停运小时数；P为统计期间小时数；F为强迫停运小时数；E2为等效强迫降低出力小时数；E3为等效强迫降低出力备用停机小时数.

将以上4个主要因素作为火电机组的可靠性评价指标［10］，即指标个数p＝4，数据如表1所示，每个样本号i分别对应一个所属集团的机组.

《汇总表》由中国电力企业联合会审查，因此，运用表中提供数据所建立的等级评价模型具有科学有效性.

2.2 指标集的归一化处理

利用式（1）和式（2）对表1中数据进行归一化处理，结果如表2所示.

2.3 优化寻求最佳投影方向a＊

2.3.1 构造投影指标函数Q（a）

为使局部投影点尽可能密集，最后凝聚成若干个点团，而在整体上投影点团之间又尽可能散开，构造投影指标函数Q（a）为：

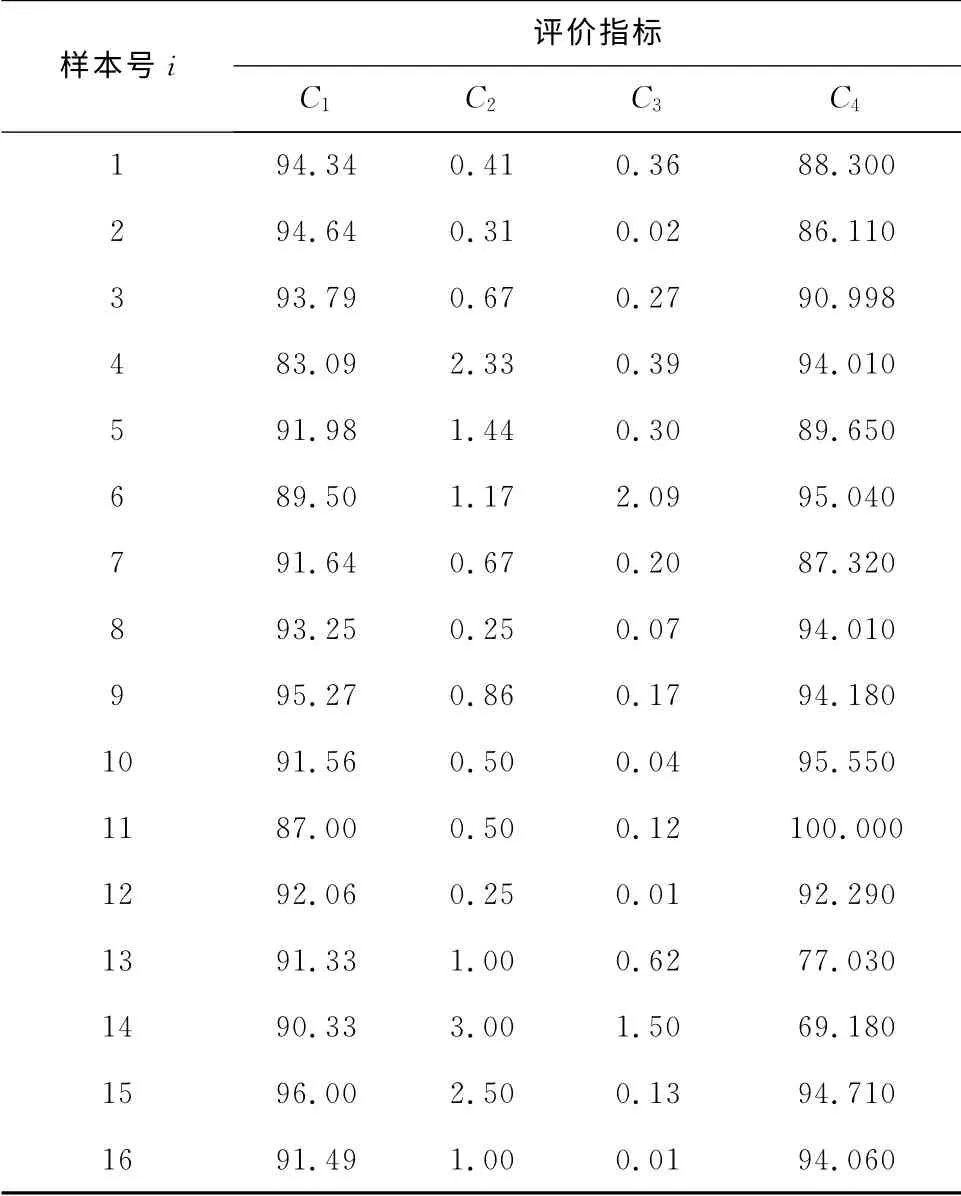
表1 模型的样本指标集Tab.1 Sample indicator set of model %

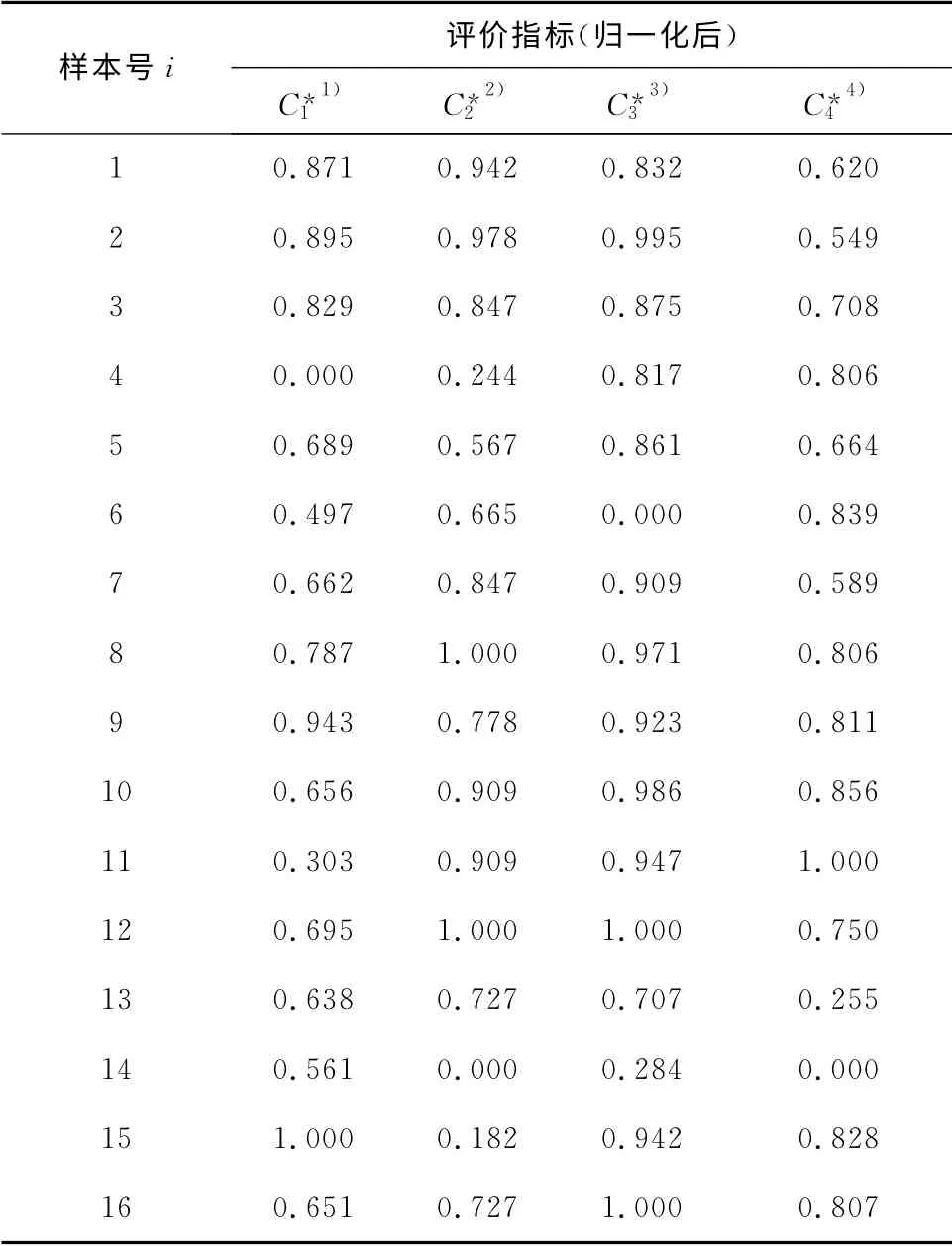
表2 归一化后的模型样本指标集Tab.2 Normalized sample indicator set of model%

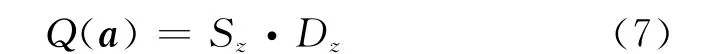
式中：Sz为投影值z（i）的标准差；Dz为投影值z（i）的局部密度.

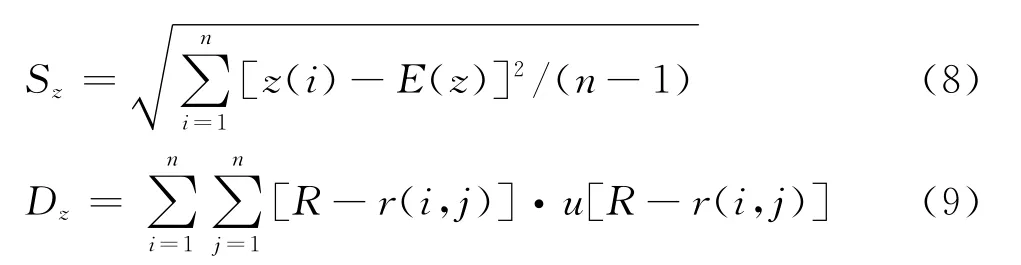
式中：E（z）为序列z（i）的平均值；R为局部密度的窗口半径；r（i，j）为样本之间的距离；u（t）为单位阶跃函数，当t≥0时，其值为1，当t＜0时，其值为0.

2.3.2 局部密度的窗口半径R的确定

用上述方法构造投影指标函数时，投影寻踪模型中唯一需要考虑的参数便是R.它的选取既要使包含在视窗内的样本点个数不能太少，以免样本滑动平均时的偏差太大；同时R又不能随样本数目的增加而增加太大.因此，将R的合理取值范围定在（rmax＋p／2）≤R≤2p内，其中，rmax＝max（r（i，j）），-p≤z（i）≤p.

经计算得rmax＝1.44，p＝1.75，因此，2.315≤R≤3.5，最终取R＝3.

2.3.3 最佳投影方向a＊的寻优

优化投影指标函数Q（a）来寻求最佳投影方向a＊，实质上是一个以｛a（j）｜j＝1，2，…，p｝为优化变量的复杂非线性优化问题，采用具有全局优化特点的遗传算法来解决此高维寻优问题.

以投影指标函数Q（a）作为适应度函数fitness，经过339代搜索寻优后，Q（a）达到最大，得到最佳投影 方 向a＊＝（0.269 9，0.676 4，0.565 3，0.387 4）.寻优过程如图1所示.

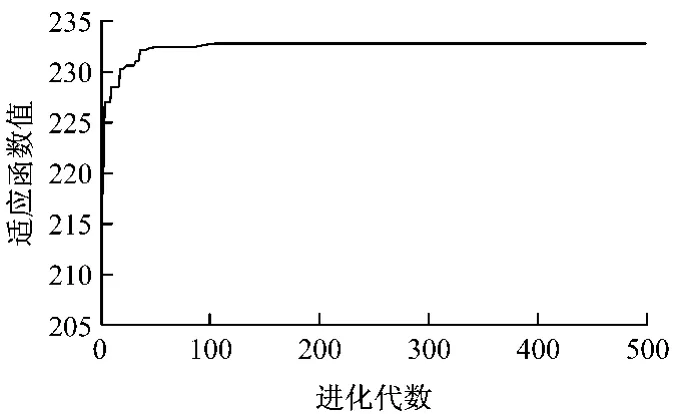
图1 遗传算法适应度函数进化曲线Fig.1 Optimization process by genetic algorithm

2.4 建立机组可靠性等级评价模型

将寻优所得最佳投影方向a＊代入式（3），可得各样本的可靠性综合指标值，即投影值z＊（j）.

z＊（j）＝（1.582 8，1.678 5，1.565 7，0.938 9，1.313 4，0.909 1，1.493 6，1.749 9，1.617 1，1.680 6，1.619 4，1.719 7，1.162 3，0.311 8，1.246 5，1.545 6）.

将16个样本的投影值按从小到大的顺序排序后，其值分布图见图2.

由图2可看出，样本的投影值集中成点团，且呈阶梯分布.因此，按照图中散布规律，划分出评价模型的3 个等级T（z），即高、中、低三级，分别用T（z）＝I、T（z）＝II、T（z）＝III代表.

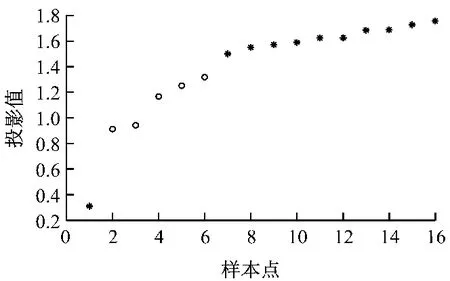
图2 可靠性综合指标值散布图Fig.2 Overall distribution of reliability indicator

运用模糊集理论［11］，结合本文算例中所得投影值z，构造各等级的隶属函数μ（z）.其中，I级隶属函数μI（z）为升半岭型，II级隶属函数μII（z）为岭型，III级隶属函数μIII（z）为降半岭型，即：

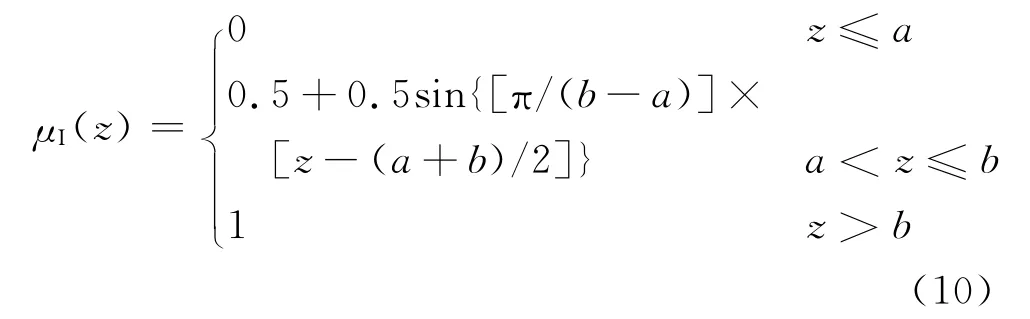
式中：a＝1.313 3；b＝1.493 6.

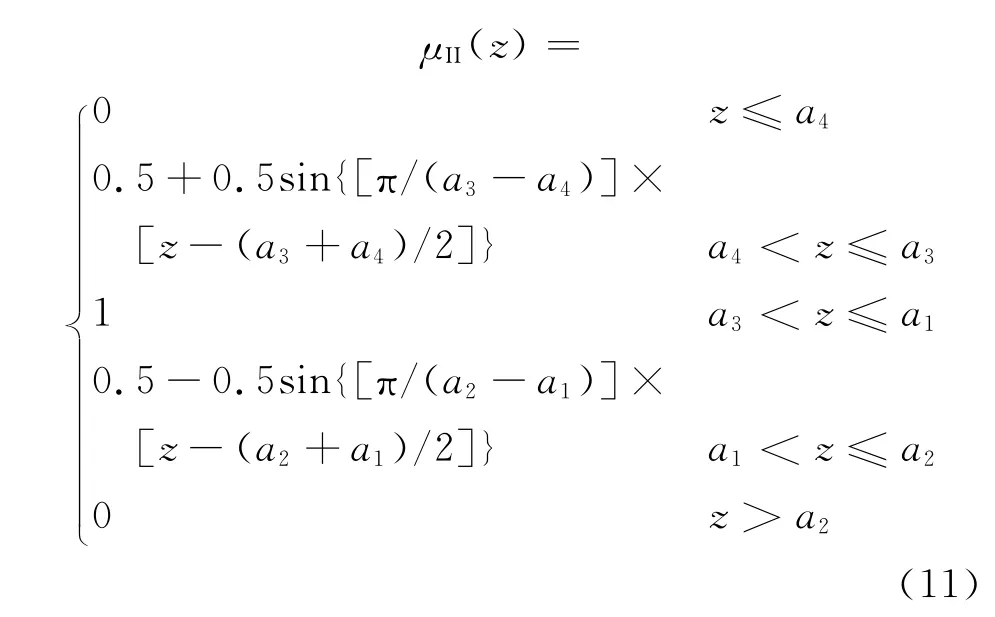
式中：a1＝1.313 3；a2＝1.493 6；a3＝0.909 2；a4＝0.311 7.

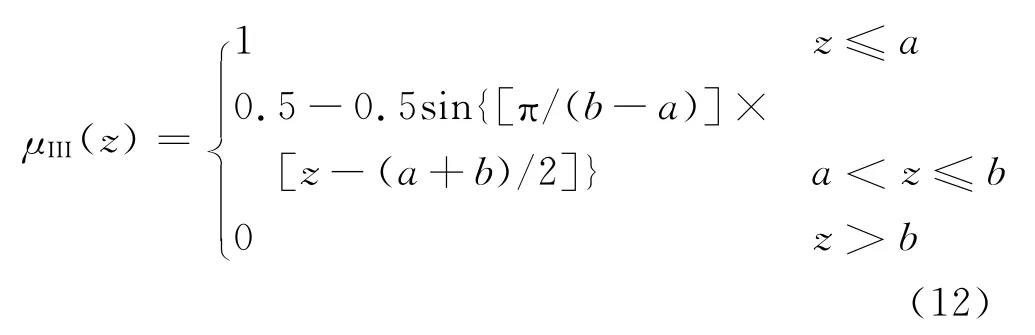
式中：a＝0.311 7；b＝0.909 2.

三级隶属函数分布如图3所示.

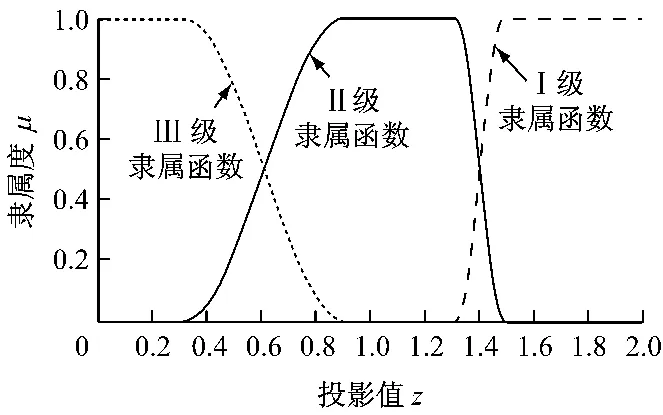
图3 各级隶属函数分布图Fig.3 Distribution map of membership function at all levels

综合以上三级隶属函数，建立等级评价模型T（z）为：

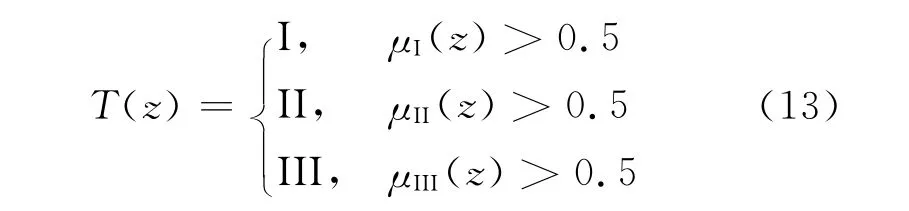
式中：μ（z）为各级隶属度值；z为待评价机组的综合指标值：z＝a·x；a为所求得的最佳投影方向：a＝（0.269 9，0.676 4，0.565 3，0.387 4）；x为待评价机组的运行参数向量.

综上所述，式（10）～式（13）为所建立的完整的可靠性等级评价模型.

2.5 模型的可行性分析

2.5.1 模型等级评价与竞赛结果的对比

表3给出了模型样本的分析数据表.

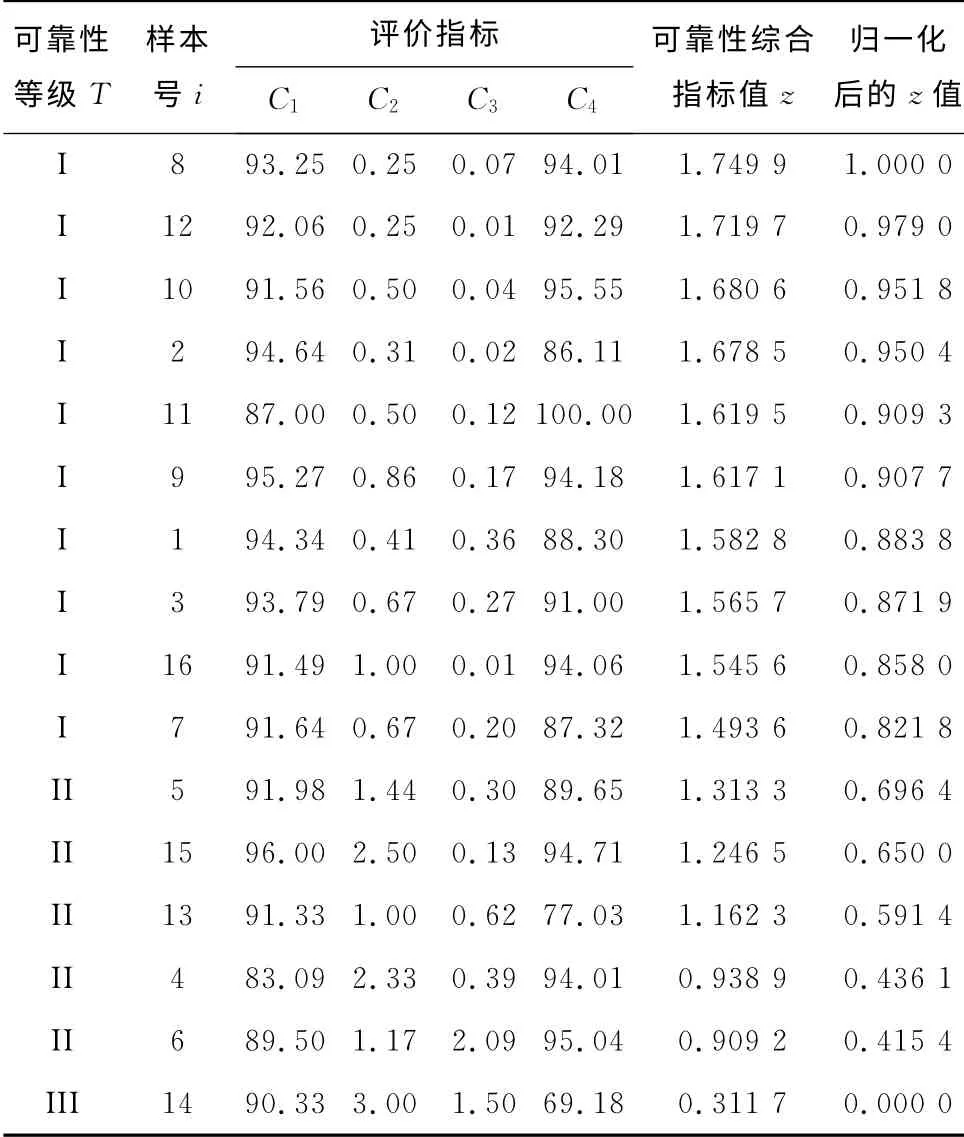
表3 模型样本分析数据表Tab.3 Analysis results of the model samples

在中电联公布的“2010年度全国火力发电可靠性金牌机组”的竞赛结果中，有10台为600 MW 级可靠性金牌机组.其中，7台机组所属的发电集团在本文的等级评价结果中属于高级（T（z）＝I），说明基于投影寻踪原理的机组可靠性等级评价结果与机组竞赛发布结果基本一致.分析其差异原因，有以下2点：（1）竞赛结果是针对全国600 MW 级的全部火电机组进行的可靠性指标评议；而本文所建立的模型仅针对全国600 MW 级的超临界火电机组进行可靠性等级评价，因此结果存在差异.（2）竞赛结果主要基于专家评议来决定机组可靠性各影响因素间的权重系数，评议结果因人而异，没有统一标准；而本文采用的方法是从高维数据本身的结构特点出发，通过投影降维处理，充分挖掘数据组在多重评价指标下的序列差异，从而完成样本的等级评价.

2.5.2 模型的可行性分析

由表3中可以看出，可靠性越高的机组，其C1、C4的值均很高，而C2、C3值普遍很低.这与机组实际的可靠性原则相吻合，即可靠性高的机组，其等效可用系数（C1）和运行暴露率（C4）高，而非计划停运次数（C2）和等效强迫停运率（C3）低.因此，分析结果表明所建立的等级评价模型与机组的实际可靠性状态完全相符，准确有效，具有可行性.

3 结 论

运用投影寻踪原理，并通过遗传算法进行全局寻优，最终得到最佳投影方向，将多维数据降维投影至一维综合指标值，从而建立火电机组可靠性等级评价模型.

与专家评议不同，基于投影寻踪方法所建模型避免了因人为赋权而造成的评价偏差，具有较强的客观性；通过机组已知的运行指标数据，代入模型便可得知设备的可靠性等级，可操作性强；通过对机组实际的可靠性状态分析，可靠性T越高的机组，其C1、C4的值均很高而C2、C3值普遍很低.

［1］左晓文，周宏.2008年全国发电可靠性统计分析［J］.中国电力，2009，42（11）：1-9.ZUO Xiaowen，ZHOU Hong.Statistic analysis on the reliability of China＇s power generation in 2008［J］.Electric Power，2009，42（11）：1-9.

［2］朱萍，徐鸿，杨昆，等.发电机组可靠性评估的研究［J］.中国电力，2003，36（8）：4-7.ZHU Ping，XU Hong，YANG Kun，etal.Study of reliability evaluation of generating unit［J］.Electric Power，2003，36（8）：4-7.

［3］杨栋，朱萍，蔡宏伟.可靠性评估在火电机组中的应用［J］.中国电力教育，2005（增刊2）：127-129.YANG Dong，ZHU Ping，CAI Hongwei.The application of reliability assessment in the thermal power u-nits［J］.China Electric Power Education，2005（s2）：127-129.

［4］侯坚坚，李元戎，刘静.基于物元分析的火电厂发电机组运行可靠性评价［J］.中国电力教育，2007（增刊2）：235-237.HOU Jianjian，LI Yuanrong，LIU Jing.Reliability evaluation of the power plant generating set based on matter element analysis［J］.China Electric Power Education，2007（s2）：235-237.

［5］付强，赵小勇.投影寻踪模型原理及其应用［M］.北京：科学出版社，2006.

［6］佚名.全国火电600 MW 级2010年机组竞赛运行数据汇总表［J］.电力技术，2010，19（7）：76-79.Anon.Summary sheet of the national thermal power 600MW units competition operation data in 2010［J］.Electric Power Technology，2010，19（7）：76-79.

［7］史进渊，杨宇，朱月祥，等.大型火电机组可靠性的增长模型和现场验证［J］.中国电机工程学报，2000，20（2）：39-41.SHI Jinyuan，YANG Yu，ZHU Yuexiang，etal.A reliability growth model for large capacity fossil fired verification with field data［J］.Proceedings of the CSEE，2000，20（2）：39-41.

［8］马传利，张克，张秋福.大型火电机组可靠性分析技术的研究［J］.动力工程，2001，21（5）：1383-1386.MA Chuanli，ZHANG Ke，ZHANG Qiufu.Research on reliability analysis technology for large capacity fossil-fired generating units［J］.Journal of Power Engineering，2001，21（5）：1383-1386.

［9］史进渊，杨宇，王兴平，等.北美发电机组可靠性的计算公式及统计结果［J］.发电设备，2004，18（3）：174-178.SHI Jinyuan，YANG Yu，WANG Xingping，etal.Reliability calculation formula and statistical results of generator sets in North America［J］.Power Equipment，2004，18（3）：174-178.

［10］史进渊，杨宇，邓志成，等.电站汽轮机研制与生产的可靠性技术研究［J］.动力工程，2005，25（1）：7-12.SHI Jinyuan，YANG Yu，DENG Zhicheng，etal.Research on reliability techniques in steam turbine development and production［J］.Journal of Power Engineering，2005，25（1）：7-12.

［11］牛培峰，孟凡东，陈贵林，等.直接型自适应模糊控制器的设计及其在汽温控制中的应用［J］.动力工程学报，2010，30（1）：22-26.NIU Peifeng，MENG Fandong，CHEN Guilin，etal.Desigh of direct adaptive fuzzy controller and its application for steam temperature control［J］.Journal of Chinese Society of Power Engineering，2010，30（1）：22-26.