基于骑士巡游的灰度图像加密压缩算法

刘博文，柏 森，刘程浩，杜鹤峣

(1.重庆通信学院应急通信重庆市重点实验室，重庆 400035;2.西南医院健康体检中心，重庆 400050)

随着计算机网络技术和数字图像技术的飞速发展，数字图像已经成为人们获取信息的重要来源，并成为人们生活中传递信息的重要组成部分。人们对图像信息的传输效率、安全性等方面也提出了更多要求，各种图像加密算法［1］也应运而生。现有的图像加密算法中，有基于空间域的，也有基于变换域的。前者算法简单、直观，但其经过加密后，像素之间的相关性会遭到破坏，以致压缩率降低。由于变换域上任意一个系数发生变化，就会引起图像原空间中的所有像素点发生变化，因而基于变换域的算法加密效率较高［2］。以往大量的工作，都只针对压缩或加密单方面进行研究与算法设计，而这对于某些对图像数据量有较高要求的信息来说，是无法满足的。为了提高传输大量图像信息的效率，同时又具有一定安全性，数字图像加密和压缩结合的技术成为了当前国内外研究的热点。

目前，在变换域中实现图像加密压缩的文献较少［3-6］。文献［3］较早做了在DCT变换域中实现图像加密压缩的工作，但出现加密后的系数不在原始系数的取值区间，且不能表示成2的幂的形式，无法简单地用诸如异或运算等方式实现加密。文献［4］给出的是一种只对非零系数进行加密的方法，其加密压缩的效果并不能令人满意，所以人为地对数据进行选择性加密会影响其安全性。文献［5］解决了加密后的系数落在原始系数区间的问题，但效率较低，加密运算需要迭代次数过多，并且使用一维混沌序列的加密强度还有待加强。文献［6］中提到的CWF算法在小波域中进行加密压缩，但其破坏了小波变换的多尺度分解树型结构，势必严重影响图像的可压缩性。

为了保证图像信息的安全性和压缩效率，笔者对图像加密压缩进行了研究，提出一种基于骑士巡游的灰度图像加密压缩方法。首先对原始图像进行8×8分块操作，再对每个8×8块进行DCT变换，产生的一个系数块化矩阵;然后对该系数块化矩阵采用骑士巡游进行以块为单位的置乱加密;最后经压缩后得到加密压缩图像。这样得到的加密压缩图像既能保证一定的安全性，又能保证较高的压缩率。

1 骑士巡游及置乱加密原理

18世纪50年代末，著名数学家Euler［7］率先提出了骑士巡游问题。骑士巡游问题 (Knight’s Tour Problem)，简称KTP，来源于国际象棋，就是骑士(马)从棋盘上的某个初始棋格开始，以跳“斜日”的方式跳遍棋盘上的每个棋格一次仅且一次的一种方案［8］。骑士的巡游只由少数几个参数(骑士巡游起始位置、巡游规则等)控制。在棋盘上建立坐标系，将棋盘左上角视为原点，棋盘上的每一格视为对应坐标系上一个点。则骑士巡游起始位置k1(x，y)就表示骑士从(x，y)格上开始移动。巡游规则k2［i，j］表示骑士每次移动的方法，即水平方向跳 i个棋格，垂直方向跳 j个棋格，或相反。例如 k1(1，1)，k2［1，2］的骑士巡游如图1a所示。一个m×n的棋盘上骑士巡游路径可以用骑士巡游矩阵T进行表示，其中矩阵T中1表示骑士巡游的起点，mn表示巡游的终点。例如，一个8 ×8 棋盘上 k1(1，2)，k2［1，2］的骑士巡游路径可以用图1b所示的矩阵来表示。其中，第1行第2列的元素1表示骑士巡游的起点，第1行第1列的元素64表示骑士巡游的终点，t表示骑士第t步所处棋盘上的位置，t=1，2，…，64。置乱加密基本原理就是将矩阵T中位置1的元素移动到位置2，位置2的元素移动到位置3，以此类推，最后将位置mn的元素移到位置1上。

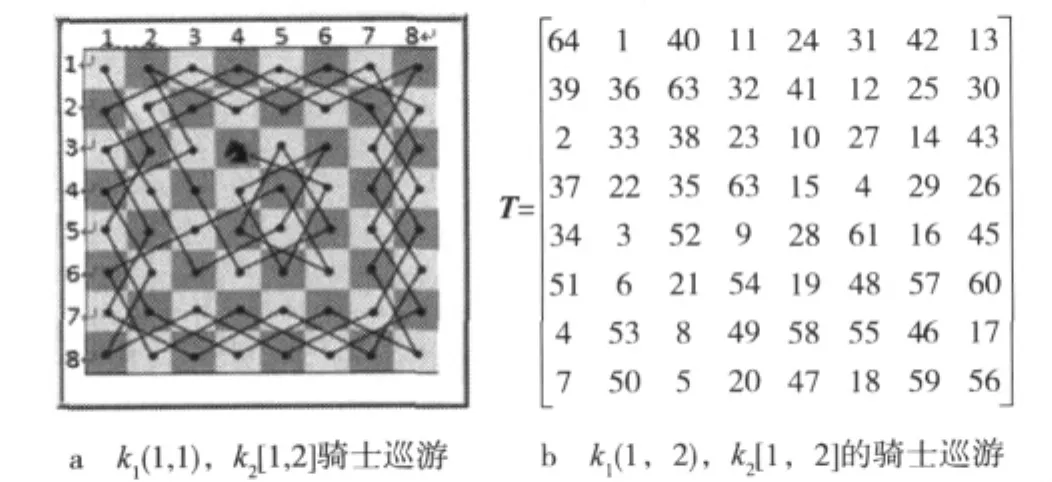
图1 骑士巡游示意图

经多年来的研究表明，骑士巡游在图像加密上的应用［9-10］效果非常好。笔者在骑士巡游置乱加密图像的基础上，将加密与压缩结合，研究新的图像加密压缩算法。

2 基于骑士巡游的图像加密压缩算法

2.1 算法思想

由于图像JPEG压缩中的DCT变换是以8×8作为最小单元进行变换。因此本文提出的算法将原始图像进行8×8分块操作后，对块化后的图像进行DCT变换得到系数块化矩阵。将系数块化矩阵中的每一块视为棋盘上的棋格，按照骑士的移动规则对每块进行移动，以实现图像中的块置乱。再经JPEG压缩后，就得到加密压缩图像。这样，由于块化操作，使得每一个小块内依然具有原有的相关性，就能很好地防止压缩率降低的问题。

这里提出一种加密压缩流程，如图2所示。

2.2 原理与步骤

设原始图像为 Im×n，加密后图像为 I'm×n，加密压缩后图像为I″m×n。本文加密压缩算法表述如下:

图2 加密压缩流程图

1)读取原始灰度图像Im×n，对其先进行8×8分块，将图像分成k×l个小块，然后对每一块进行DCT变换后，得到系数块化矩阵 Ck×l。其中，k=⎿m/8」，l=⎿n/8」，⎿」表示下取整。

2)根据前面第2节的介绍，选择起始位置k1(x，y)、巡游规则k2［i，j］作为初始密钥，使用文献［11］中的算法得到骑士巡游矩阵Tk×l。

3)将 Ck×l中每个8 ×8 块看成 Tk×l上的一格，使 Ck×l与Tk×l中元素一一对应。根据骑士巡游置乱原理进行骑士巡游块置乱，得到加密后的系数块化矩阵C'k×l。

4)对C'k×l进行DCT逆变换，将逆变换后的数据块化还原，得到加密后图像I'm×n。

5)令 Im×n=I'm×n，重复步骤1)至5)，直至得到满意的加密效果为止。最后将I'm×n进行JPEG压缩，得到最终加密压缩图像 I″m×n。

解密是上述过程的逆过程。

3 算法仿真与评价

3.1 直观效果

通过对256×256的Lena和Baboon两幅测试图像进行5 次循环加密实验，设置初始密钥 k1(1，1)，k2［1，2］和k1(1，2)，k2［1，4］，其加密压缩效果分别如图3 和图4。

图3 Lena图像加密压缩效果图

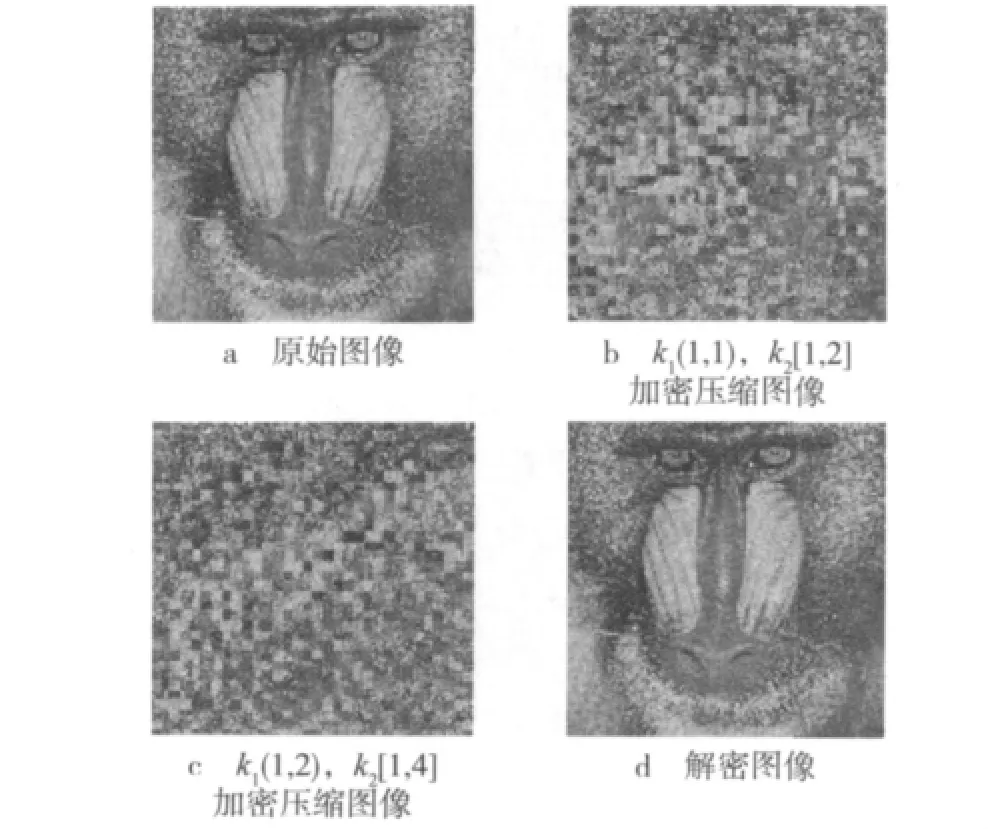
图4 Baboon图像加密压缩效果图

可以看出基于骑士巡游的加密压缩方案得到了较好的加密效果，而且解密的效果理想。

3.2 置乱度

置乱度(SM)用来评估图像被置乱或加密程度，即图像加密的直观效果好坏的重要指标，它能较为客观地反映图像的加密效果。目前，许多文献都给出了置乱度的定义，但又各不相同。这里引用文献［12］中定义的置乱度来评估图像的置乱或加密程度，其计算式为

式中:I={Iij}M×N表示原始图像，～I={～Iij}M×N表示置乱或加密图像，R={Rij}M×N表示与原始图像相同大小的均匀分布噪声图像。为了使得加密图像的置乱度具有可比性，通常采用同一幅均匀分布的噪声图像。本文取k1(1，1)，k2［1，2］为密钥，得到的实验结果如表1。

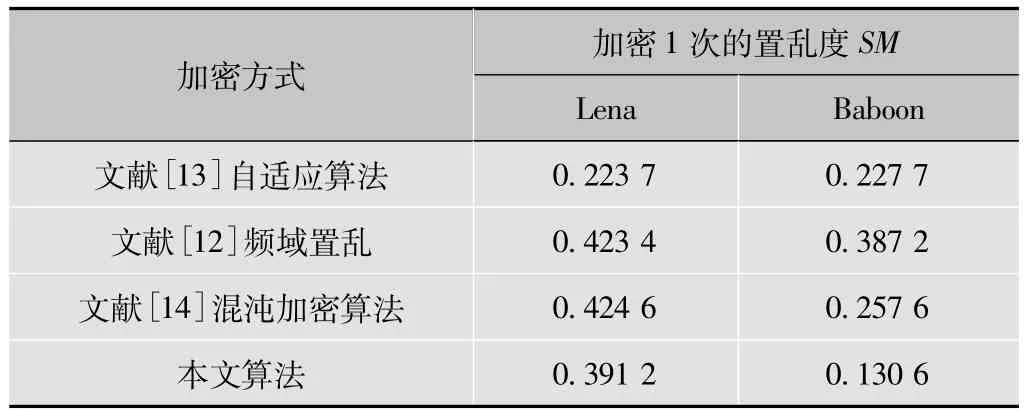
表1 加密后图像的置乱度

为了提高算法的压缩率，采用了块化操作，这使得加密置乱的单位是8×8块而不是单个像素，从而导致加密的置乱度有一定下降，可通过增加循环加密次数来解决置乱度较低的问题。

3.3 压缩率

压缩率作为图像压缩的一个评价指标，其计算式为

在压缩率测试中，采用256×256的Lena图像进行测试。算法选择k1(1，1)，k2［1，2］的骑士巡游矩阵作为密钥，文献［15］采用阈值为100时的最好效果，经过1次加密后得到压缩率如表2所示。

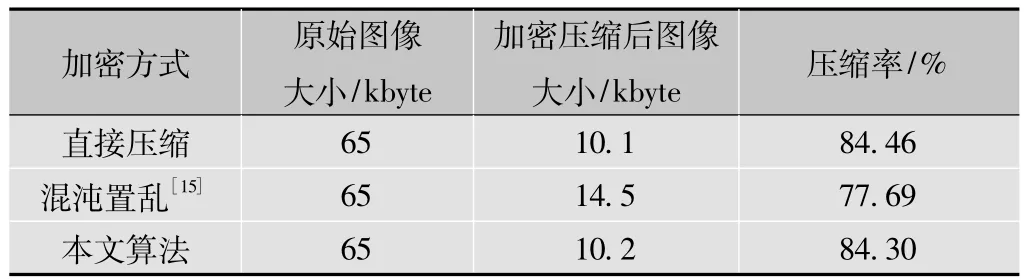
表2 压缩效率比较

随着本文算法加密次数的增加，压缩率将保持不变。其结果如表3。

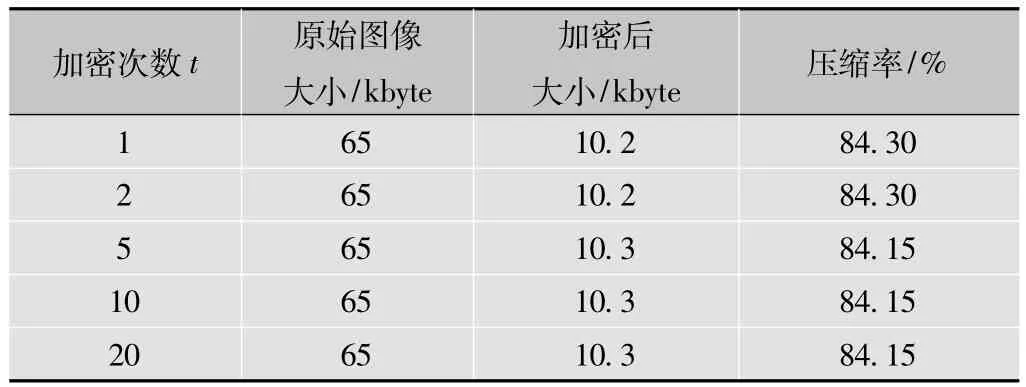
表3 加密次数与压缩率

可以看出，采用基于骑士巡游的灰度图像加密压缩算法在压缩性上较文献［15］提高了不少，接近对原始图像直接压缩的效果。并随着加密次数的增加，压缩率基本保持不变。因此选取加密次数为5次，以节约运算时间。

3.4 安全性分析

骑士巡游矩阵作为密钥时，其密钥空间如表4所示。

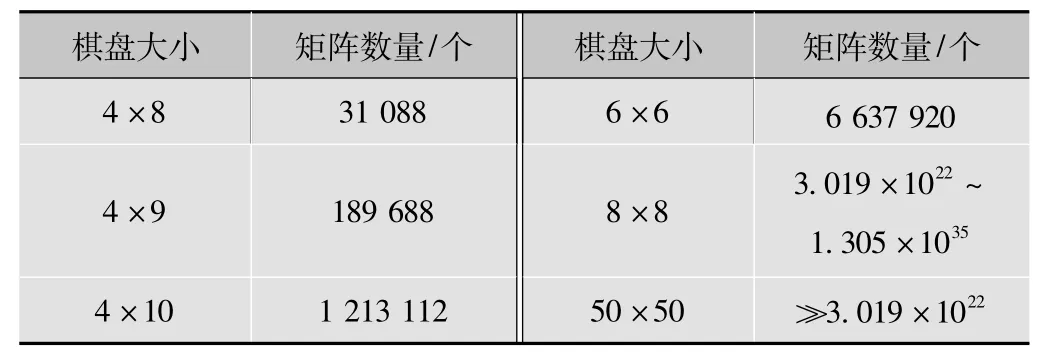
表4 骑士巡游矩阵数量统计表［16］

结果表明，对于一个8×8的棋盘，其拥有的骑士巡游矩阵的数量至少3.019×1022个。由于人眼可以分辨其内容的图像大小一般为50×50以上，所以用骑士巡游矩阵作为图像加密的密钥，其密钥量将会是个天文数字。换个角度来说，用骑士巡游矩阵作为密钥时，其密钥空间足够大。

图像加密还要求较高的密钥敏感性，即密钥之间发生变化时，就能够导致解密失败。这样就能保证密码系统针对穷举攻击、统计攻击的安全性。这里使用初始密钥k1(1，1)，k2［1，2］进行一次图像加密，分别用密钥 k1(1，2)，k2［1，2］和 k1(1，1)，k2［1，4］解密 Lena 图像，其解密效果如图5所示。

图5 Lena图像解密效果图

仿真实验表明，骑士巡游矩阵的密钥发生变化时，就无法正确解密出原始图像。因此，本文的加密压缩算法对骑士巡游棋盘密钥具有很好的敏感性。

4 结束语

本文提出的一种基于骑士巡游的图像加密压缩算法，实现了具有加密效果较好、密钥空间大、密钥敏感性强等优点的加密压缩方法。通过在变换域中使用骑士巡游块置乱加密，在保证一定安全性的前提下，降低了加密对压缩效率的影响。经实验证实将加密和压缩相结合，既能保证传输涉密图像的安全性，又能大大提高存储和传输效率。在图像信息的发布与交流越来越普及的今天，该方法具有很好的应用前景。

［1］李昌刚，韩正之，张浩然.图像加密技术综述［J］.计算机研究与发展，2002，39(17):1317-1324.

［2］李娟，冯勇，杨旭强.压缩图像的三维混沌加密算法［J］.光学学报，2010，30(2):399-404.

［3］孙鑫，易开祥，孙优贤.基于混沌系统的图像加密算法［J］.计算机辅助设计与图形学学报，2002，14(2):136-139.

［4］李兴华，高飞.一种基于混沌序列的数字图像加密算法［J］.电讯技术，2006，46(1):99-104.

［5］彭成，柳林.基于混沌序列的压缩图像加密算法［J］.计算机工程，2008，34(20):177-179.

［6］平亮，孙军，周军.一种基于JEPG2000标准的数字图像加密算法［J］.电视技术，2006，30(7):87-90.

［7］EULER L.Solution d’une question curieuse qui ne parait soumise à aucune analyse［M］.Berlin:Mémoire de I’Académie Royale des Scìences XV，1759:310-337.

［8］PARBERRY I.An efficient algorithm for the knight's tour problem［J］.Discrete Applied Mathematics，1997，73(3):251-260.

［9］柏森，曹长修.一种新的数字图像置乱隐藏算法［J］.计算机工程，2001，27(11):18-19.

［10］姜德雷，柏森，董文明.基于广义骑士巡游的图像比特位平面间置乱算法［J］.自然科学进展，2009，19(6):691-696.

［11］BAI Sen，LIAO Xiaofeng，QU Xiaohong，et al.Generalized knight’s tour problem and its solutions algorithm［C］//Proc.2006 International Conference on Computational Intelligence and Security:Part I.［S.l.］:IEEE Press，2006:570-573.

［12］侯启槟，杨小帆，王阳生，等.一种基于小波变换和骑士巡游的图像置乱算法［J］.计算机研究与发展，2004，41(2):369-375.

［13］CHEN G，ZHAO X Y，LI J L.A self-adaptive algorithm on image encryption［J］.Journal of Software，2005，16(11):1975-1982.

［14］MAO Y B，CHEN G，LIAN S G.A novel fast image encryption scheme based on the 3D chaotic barker map［J］.Int.J.Bifurcat Chaos，2004，14(10):3613-3624.

［15］邓绍江，濮忠良，张岱固.基于小波压缩和混沌置乱的图像处理算法［J］.重庆大学学报，2008，31(8):918-921.

［16］姜德雷.基于骑士巡游的图像和视频加密技术研究［D］.重庆:重庆通信学院，2009:61-62.