城市轨道线路设计三维地下结构造型算法
王明生 施仲衡
(1.北京交通大学土木建筑工程学院 北京 100044;2.石家庄铁道大学交通运输学院 石家庄 050043)
1 城市轨道交通选线设计概况
选线设计是城市轨道交通系统规划设计工作中的核心环节,具有牵涉面广、复杂性强、责任重大等特点[1]。线路走向与空间位置选择合理与否,将直接影响到工程实施的难易程度及运营后的客流效益。由于城市轨道交通线路多处于城市中心区,地上建筑物和地下构筑物情况复杂,线路设计中容易发生与既有建筑物和各种设施设备的位置冲突。现有的选线设计方法多是基于地形平面图和调查勘探资料,在二维设计环境下进行的平、纵交替设计,不易直观地发现各种潜在的冲突,需要内外业反复验证,不仅设计效率低下,且容易造成设计缺陷,难以满足城市轨道交通选线设计工作的需求。随着现代信息技术的发展,将遥感技术、数字摄影测量技术、虚拟现实技术、数字地质技术等综合集成,建立一个能够满足复杂城市环境下轨道交通选线要求的三维可视化选线设计系统,让工程师在逼真显示的三维可视化环境中进行选线方案设计与决策,已成为城市轨道交通选线设计信息化发展的趋势[2]。
城市轨道交通三维可视化选线设计系统的核心技术是为各种实体建立三维显示模型。目前,在铁路线路三维可视化设计的理论研究与实践方面已经取得了较大进展,对于地形场景生成[3]、路基和桥梁等构筑物建模[4]以及地质体三维建模[5]等已经有了比较完善的模型和算法,这些模型与算法稍加改造即可用于城市轨道交通三维选线设计系统中。但是,城市轨道交通选线设计有其自身的特点,即在城市环境中地下构筑物结构复杂,潜在冲突多,在三维环境下为地下结构进行准确、快速地建模是一个关键问题。目前,在地下构筑物的三维造型方面还缺少准确高效的算法。针对这一问题,笔者结合城市轨道交通三维可视化选线设计的特点,提出了一种高效的地下结构三维造型算法,并结合OpenGL平台探讨了三维造型算法中坐标变换这一核心问题。
2 地下结构三维造型算法基本思路
在城市轨道交通线路设计中,涉及的地下构筑物主要有地下隧道、建筑物桩基和各种市政管线设施。这些构筑物的断面形式(马蹄形、圆形或矩形等)虽然有所不同,但都可以抽象为由直线段和曲线段连接而成的管状实体。在对这类管状实体进行三维表达时,对于直线段的建模比较简单,难点在于对曲线段的处理。对于这一问题目前的解决方法主要有两种:一种方法是直接绘制相接的两条直线管段,再在衔接处进行剪裁处理[6],这种方法思路简单,但接头处有棱角,外观不光滑;另外一种方法是用球体表达衔接点[7],这种方法简单易行,但由于模型外观与实际相差太大,对于地铁隧道等特殊的管状实体不适用。
针对上述问题,笔者提出一种用四边形面片近似描述管状实体的方法,其核心思想是使用一系列相互衔接的四边形面片来近似表达管状实体的外部表面。该方法首先将管状实体的任意截面形状细化成符合精度要求的多边形,而后对于每个直线段管状实体,可以简化成两端不等截面积的多棱台,剖分成四边形面片进行绘制;而对于曲线段管状实体,则按照分段直线绘制,每段形状类似多棱台,但两端是沿曲线法线的截面(见图1)。在OpenGL平台中绘制管线时,需要先建立从原点向Z轴正向绘制直线管状实体的函数。对于曲线部分,则需要沿中线将其分段剖分成多段折线,再经过坐标变换,把每段都变成从原点向Z轴正向可分段调用直线段的绘制函数。在剖分截面和中线时,分段数量取决于所要求的显示精度,数量越多则弯管表面越光滑。在实际应用中,可以根据显示比例调整分段数量,以在显示精度和计算量之间获取平衡。
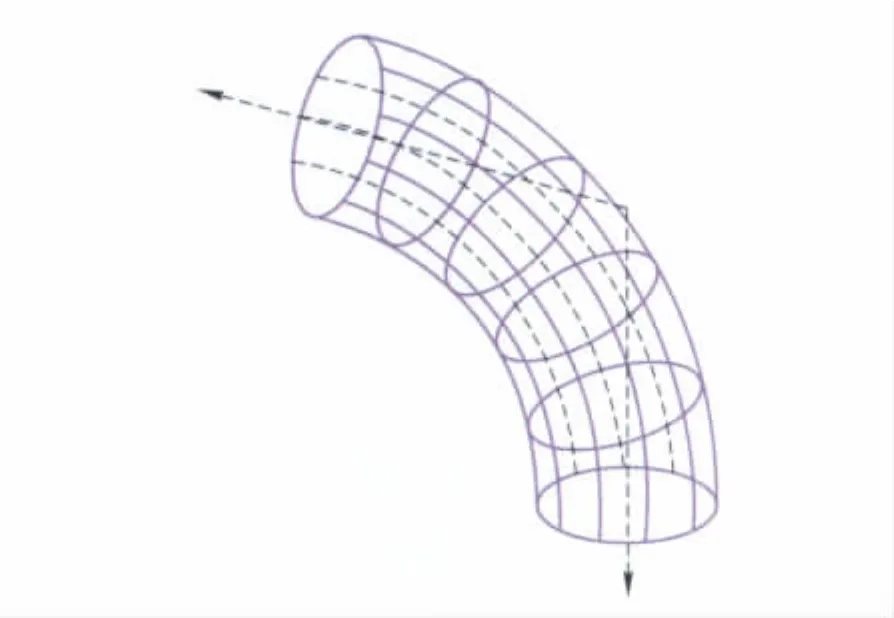
图1 用四边形面片近似描述管状实体
3 基于OpenGL平台的坐标变换方法
用四边形面片近似表达管状体表面的关键是准确计算四边形各顶点的坐标。由于不同的三维图形开发平台采用的坐标系有所不同,具体的实现方法也有所区别。OpenGL[8]是目前使用较为普遍的一个三维图形开发平台,它独立于窗口系统和操作系统,以它为基础开发的应用程序可以十分方便地在各种平台间移植。因此,下面结合OpenGL平台对三维管状体绘制过程中的坐标变换问题进行探讨。
OpenGL的坐标系可以分为世界坐标系和局部坐标系两种。世界坐标系是以屏幕中心为原点,右边是X轴正方向,上面是Y轴正方向,垂直于屏幕指向屏幕外的方向为Z轴正方向,世界坐标系是固定不变的。局部坐标系是绘制物体时的坐标系,它以物体中心为坐标原点,物体的旋转或平移等操作都是围绕局部坐标系进行的。当物体模型进行旋转或平移等操作时,局部坐标系也执行相应的旋转或平移操作。在OpenGL下实现局部坐标系的平移和旋转需要用到glTranslatef(x,y,z)和 glRotatef(angle,x,y,z)两个函数[8]。glTranslatef(x,y,z)函数的作用是将局部坐标系原点在当前原点的基础上平移一个(x,y,z)向量;glRotatef(angle,x,y,z)的作用是将局部坐标系沿经过原点、方向为(x,y,z)的旋转轴旋转angle角度。使用这两个函数的方便之处在于省却了坐标平移和旋转过程中复杂的矩阵运算,开发人员只需根据预先设定的变换步骤,调用相应的函数即可实现局部坐标的旋转平移操作。
结合OpenGL提供的上述两个坐标变换函数,可以得到绘制管状实体曲线段的具体过程。此处将某一曲线段两端衔接的直线管段中心线的矢量方向分别记为V1和V2,将局部坐标系的3个方向分别记为 X,Y,Z。在绘制管状实体曲线段的过程中,需要首先将第一段直线管段的末端(x1,y1,z1)平移至局部坐标系原点,然后进行3次坐标旋转变换。
1)将V1-V2平面沿 V1轴转到 Z-V1平面,转角为

式中,θ1是坐标旋转角度,nZV1是Z-V1平面法向量,nZV1=V1× Z,nV1V2是 V1- V2平面法向量,nV1V2=V1×V2。
2)将Z-V1平面沿Z轴转到Z-X平面,转角为
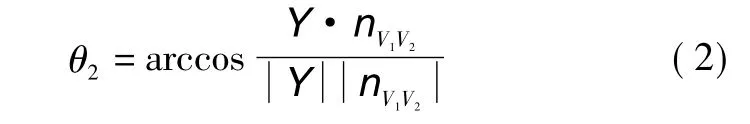
式中,θ2是坐标旋转角度,nV1V2意义同式(1)。
3)将V1方向沿Y轴转到坐标Z正向,转角为
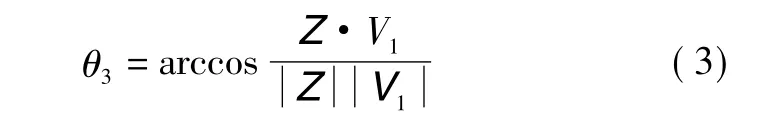
式中,θ3是坐标旋转角度。
图2是前述坐标旋转变换步骤的示意图。经过这一系列的坐标变换后,即可在当前的局部坐标系下绘制管段截面的外轮廓点,之后再将V2旋转至局部坐标系的Z轴,并将此直线段的起始端(x2,y2,z2)平移至局部坐标系原点,绘制此段管段截面的外轮廓点,并用四边形与上一步绘制的外轮廓点连接,就可绘制完成该段多棱台。重复以上步骤,就可绘制完成整个管状实体。
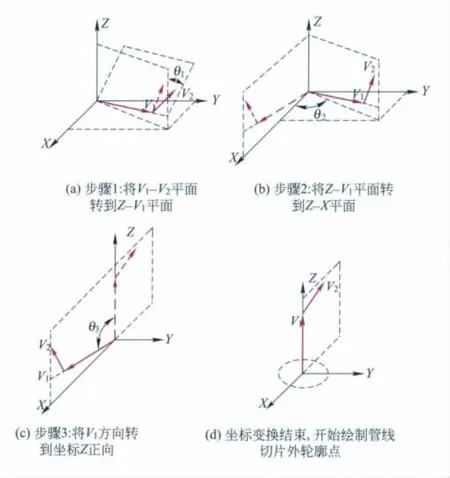
图2 坐标旋转变换步骤
4 算法实现
在OpenGL环境中实现了对前述地下结构的三维造型算法,图3为地下管线三维模型示例,图4为地下隧道三维模型。从图中可以看出,用本算法构造的地下结构三维显示模型外观光滑,曲线连接平滑顺畅,能够满足城市轨道交通三维选线设计系统对地下结构可视化的要求。


5 结语
笔者提出了一种在OpenGL环境中用四边形面片近似表达管状实体表面的方法,构造出地下结构三维模型的算法,着重对三维造型中的坐标变换问题进行了探讨,并通过实例对所提出的算法进行了验证。结果表明,该方法可以在OpenGL环境中高效便捷地实现地下结构的三维可视化,曲线部分连接平滑顺畅,显示效果逼真。它不仅能够对圆形断面的地下管线等结构实体进行建模,还可以对地下隧道、建筑物桩基等各种非圆形断面的管状实体进行建模。同时,该方法还可以绘制两端截面积不等的管状实体以及中线为任意曲线形式的管状实体,具有较好的通用性。
[1]徐振廷.城市轨道交通线路选线设计[J].交通科技,2009(S1):96-98.
[2]吕希奎.基于遥感信息的选线系统地理环境建模方法及应用研究[D].成都:西南交通大学,2008.
[3]吕希奎,易思蓉,韩春华.大规模地形真三维可视化系统设计与实现[J].计算机应用研究,2008,25(2):603-609.
[4]王明生,张振平.基于GIS的铁路路基三维可视化技术研究[J].工程图学学报,2009,30(1):66-69.
[5]赵宁.三维铁路工程地质建模研究[D].成都:成都理工大学,2008.
[6]宋能,曹菡.基于OpenGL的空间管线的拼接显示与应用[J].计算机工程与科学,2008,30(11):144-146.
[7]柯新利.OpenGL三维管线绘制中的坐标变换研究[J].地理空间信息,2008,6(3):53-55.
[8]Shreiner D,Woo M,Neider J.OpenGL编程指南[M].邓郑祥,译.4版.北京:人民邮电出版社,2005.

