基于希尔伯特-黄变换的复杂电能质量信号检测技术

胡晓曦 刘含露 熊婷婷 胡京莹

（1.长沙理工大学电气与信息工程学院，长沙 410114；2.湖北咸宁市供电公司，湖北 咸宁 437100）

提供高可靠性、高质量的电能是智能电网建设的目标之一[1-2]。但是随着智能电网的发展，各种非线性负荷也在不断的增长，给供电系统电能质量造成严重的问题[3]；另外高智能的用电设备也对电能质量提出了更高的要求；这些电能质量问题越来越引起电力部门和电力用户的高度重视，在国家电网公司发布的《智能电网关键设备（系统）研制规划》中指出：要建设电能质量监测和治理装置[4]。

目前，国内外提取电能质量扰动信号特征量的方法主要有傅里叶变换[5]、S变换[6]、小波变换[7]等。傅里叶变换只适合平稳信号分析，无法满足对具有暂态、突变等特性的电能质量扰动的非平稳信号进行分析的要求[8]。小波变换中小波基对信号的小波变换结果影响很大。然而，目前如何选择小波基还没有统一的方法或可遵循的原则[9]。

HHT是近年来发展起来的一种信号分析的新方法[10]。它对处理非线性、非平稳信号有很明显的有效性和优越性：它没有固定的先验基底，是完全自适应的；通过Hilbert变换得到的瞬时频率具有清晰的物理意义，能够表达信号的局部特征；可以准确地揭示数据的内部特征，在时频域得到较高的分辨率，相较于其他方法可以有更好的结果。所以本文采用HHT(Hilbert-Huang Transform)变换法分别对单扰动和多扰动电能质量信号进行精确检测。

1 HHT基本原理

HHT变换主要是由两个部分构成：经验模态分解（EMD）和Hilbert变换，其广泛用于非线性非平稳信号的分析。

1.1 经验模态分解

EMD是提取信号中的IMF分量，其方法如下：首先根据信号s(t)的极大点和极小点求出其上包络线v1(t)及下包络线v2(t)的平均值m1(t)，即

将原数据序列s(t)减去m1(t)可得到一个去掉低频的新数据序列h1(t)：

重复处理以上过程k次，直到h1(t)得到的均值趋于零为止，这样就得到了第1个IMF分量c1(t)，它代表信号s(t)中最高频率的分量：

将c1(t)从s(t)中分离出来，可得到一个去掉高频分量的差值信号r1(t)，即有

将r1(t)作为原始数据，重复循环以上步骤得到第二个IMF分量c2(t)，重复n次，直到使 rn(t)成为一个单调函数，循环终止，得到n个IMF分量。这样就有

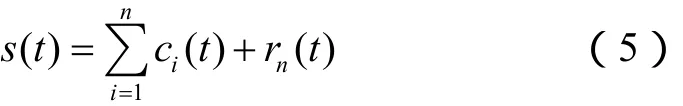
以上是 EMD分解，可以将不同频率的信号分离出来。

1.2 希尔伯特变换（Hilbert）

对IMF进行希尔伯特变换就能得到信号的时频图，能够准确找到信号突变发生的时间。设Y(t)是信号X(t)的希尔伯特变换,即

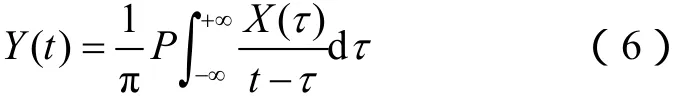
其中，P为柯西主值，它对于所有PL级函数都成立，通过这一定义，X(t)和Y(t)为复共轭对，即

可以得到解析信号Z(t)

式中，a(t)为瞬时幅值，θ(t)为相位。

瞬时频率定义为：

EMD分解和与其相应的希尔伯特变换一起被称为HHT变换。本方案用瞬时频率 f(t)来定位信号的准确时间。

2 单扰动简单信号的仿真及结果分析

电力系统中主要的电能质量问题是电压暂降和谐波问题，本文先以电压跌落和谐波单扰动状态监测为例，做电压暂降和谐波含有量HHT仿真验证。

2.1 单扰动电压暂降

在Matlab中产生标准工频信号，在不同时刻加入阶跃信号来产生电压暂降现象，电压暂降信号如图1所示。

图1 电压扰动信号

电压有效值为220V的某相线路发生电压暂降，电压暂降从发生到终止的理论时刻为 0.22s到0.63s，跌落幅度为 120V。HHT仿真得到时频关系如图2所示，时间幅度关系如图3所示。

图2 电压扰动时频关系

图3 电压扰动时间幅度关系

由图2和图3可以看出检测出来的电压暂降时间为0.218～0.627s，经计算平均暂降后的幅度峰值大概为141.92V，和理论值基本符合，根据IEEE标准此时电压暂降超过了0.1s，判断发生了电压暂降。

2.2 单扰动谐波

在Matlab中的标准工频信号中加入5次谐波信号扰动，扰动时间为 0.25～0.8s，谐波扰动信号如图4 所示。

图4 谐波扰动信号

图5 谐波扰动时频关系

通过HHT仿真得到信号时频关系如图5所示。从图5可知HHT算法能准确的检测出扰动为5次谐波扰动，起止时间为0.248～0.799s。

2.3 间谐波

而对于非整数次间谐波也可以用 HHT法来进行检测，在0.15～0.77s加入频率为工频50Hz的5.5倍幅值为80V的谐波，其谐波表达式为

其信号图如图6所示。

图6 间谐波信号图

图7 间谐波分析时频关系

对间谐波信号进行HHT分析如图7所示，由图7也可以看出检测出的频率十分接近所给定的275Hz而且起止时间的检测也是准确的。

由上述仿真，可见HHT法对于单扰动情况下的电压暂降和谐波均具有较高的灵敏度和精确度

3 复杂多扰动信号的仿真及结果分析

HHT在单一扰动情况下已经有良好的检测性，但是在电力系统中负载的复杂多样性和随机性，以及外部干扰等因素，这些非平稳的暂态信号往往交织叠加形成多扰动信号作用于正常的电力信号[11]。本文在工频50Hz，幅值有效值为220V，并带有暂态电能质量多扰动：电压暂降谐波、电压暂升谐波、电压中断谐波、多谐波的定位及幅值、频率的检测为例，运用Matlab仿真验证。

3.1 电压暂降、（暂升）谐波检测仿真

在短时发生单相电压暂降时，仿真设定相电压有效值为220V，频率为50Hz，于0.10～0.85s带有5次谐波分量，其有效值为80V；在0.30～0.65s 之间发生电压暂降，其幅值有效值为140V，暂降后幅值为原来的36.36%。电压扰动信号如图8所示。对信号进行EMD分解如图9所示。

图8 电压扰动信号

电压暂降瞬时频率如图10所示，从图10可以清楚的看出发生扰动的起止时刻和电压暂降的时刻以及谐波的频率。瞬时频率在0.201s 和0.852s 发生跳变，是5次谐波扰动，同时电压在0.306～0.653s之间发生跌落。由此可以准确地检测出电压暂降伴随谐波发生的起止时间、谐波频率、电压跌落幅度如图11所示。

图9 目标信号EMD分解

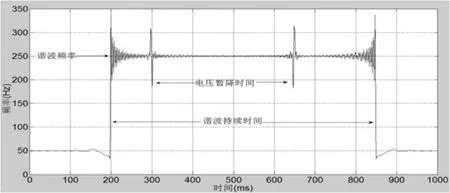
图10 电压暂降瞬时频关系

图11 电压暂降瞬时幅值

由图11可以看出发生扰动的大约起止时刻，电压暂降的峰值约为110.2V，符合工程应用要求。同样的方法可以检测电压暂升复合扰动。

3.2 电压中断谐波检测仿真

利用Matlab仿真中设定相电压有效值为220V，频率为50Hz，在0.2～0.8s之间有幅值有效值为80V的 3次谐波，并于 0.35～0.7s 之间发生电压中断，电压中断及谐波信号如图12所示。

图12 电压中断信号

对信号进行 HHT计算分析得到信号的频率时间关系如图13所示。

图13 电压中断时频关系

从图13可以看出3次谐波伴随着电压中断的出现。在 0.202～0.802s之间发生 3次谐波干扰，在0.351～0.701s发生电压中断。其误差很小，可以得到精确的中断起止时间，所以HHT检测电能质量算法在有谐波的情况下对于电压瞬时中断的检测也是正确有效的。

3.3 多次谐波频率的检测

谐波仿真中设定信号为标准工频电压信号，在不同时间加入3次、5次、7次谐波进行仿真分析，其电压谐波信号图如图14所示；谐波信号HHT分析如图15所示。

图14 电压谐波信号

图15 多次谐波的时频关系

图15中可以看出信号含有3种谐波，3次谐波发生时间为 0.101～0.402s，5次谐波扰动的起止时刻为 0.301～0.749s，7次谐波扰动的起止时刻为0.602～0.857s，和理论时刻基本相符合，采用HHT可以准确的找到谐波的含有量、起止时间。

由以上算列仿真可以得出该方法能够比较准确地检测出突变、非平稳扰动信号的时间、频率和幅值的信息。虽然由于端点效应及模态混叠和谐波等问题的影响会产生误差，但是经过多次测试，基于HHT的多扰动的电能质量检测的平均误差很小，能满足工程要求，可以说本方法对多扰动电能质量的检测是正确可行的。

4 结论

本文应用HHT算法分别对单扰动和多扰动电能质量信号进行检测分析。从理论上来讲HHT 方法实现了自适应的频带划分，信号分析更加灵活多变。

仿真表明，对检测的电能质量信号进行 EMD分解，再对得到的各IMF分量求瞬时频率，可以精确地检测到扰动信号的发生和终止时刻；结合瞬时幅值的求解方法，可以快速地检测出扰动信号的幅值；在复杂的电能质量信号下依然有很高的精确度和实时性。该方法简单快捷，易于实现，能满足工程需求，适用于电能质量多扰动的监测和辨识系统，应用前景广阔。

[1]余贻鑫,栾文鹏.智能电网述评[J].中国电机工程学报,2009,29(34):1-4.

[2]王益民. 坚强智能电网技术标准体系研究框架[J].电力系统自动化,2010,34(22):1-6.

[3]张涛,程志友,梁栋,等.非线性主成分分析在电能质量综合评估中的应用[J].电测与仪表,2008,45(6):5-9.

[4]智能电网关键设备（系统）研制规划[R].国家电网公司, 2010.

[5]徐永海，赵燕. 基于短时傅里叶变换的电能质量扰动识别与采用奇异值分解的扰动时间定位[J].电网技术, 2010,35(8):174-180.

[6]唐求,王耀南,郭斯羽,等.基于 S 变换与 PNN 的电能质量多扰动检测[J].仪器仪表学报,2009,30(8):1669-1673.

[7]石敏,张纪铃,徐袭,等.电压跌落信号参数的检测[J].微计算机信息,2010,26(35):10-11,122.

[8]HEYDT G T, FJELD P S, LIU C C, et al. Application of the windowed FFT to electric power quality assessment[J].IEEE Transactions on Power Delivery,1999,14(4):1411-1416.

[9]KEZUNOVIC M, LIAO Y. A novel software implementation concept for power quality study[J]. IEEE Transactions on Power Delivery, 2002,17(2): 544-549.

[10]李天云,程思勇,杨梅. 基于希尔伯特-黄变换的电力系统谐波分析[J].中国电机工程学报,2008,28(4): 109-113.

[11]LU Z, SMITH J S, WU Q H. Empirical mode decomposition for power quality monitoring[C].Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005. IEEE/PES.