电力线仿真系统的FPGA设计与实现
冯 恒,李树青
(西安电子科技大学电子工程学院,陕西 西安 710071)
由于配电网络具有的超大规模和电力线通信具有的成本低、覆盖广、部署便捷等特点。电力线通信提供了优良的设备互联解决方案,因而受到广泛关注,并在智能电网、Internet接入、智能家居等领域得到了广泛应用。
然而由于电力线并不是为通信而设计,对于频率较高的通信信号而言,电力线信道比较复杂和恶劣。因此建立一个标准化的测试平台对电力线通信设备的研发十分必要。对于生产商而言,这样的测试平台能在产品开发的每一步对算法性能立即进行可重复性的验证。对于用户而言,这样的平台可以帮助其在同一平台下对比不同生产商的产品性能,以便对产品做出更客观的评价。而当前缺乏这种针对物理层进行测试验证的工具,大部分针对电力线通信设备的测试主要集中在上层,由于采用多种纠错技术,所以由物理层带来的问题有可能被掩盖。
尽管目前基于顺序执行的处理器主频已经很高,但是处理深度较大的复杂数据流往往力不从心。FPGA强大的并行处理能力和灵活的可定制性为这类数据的处理提供了一个良好的解决方案。
1 系统框架
1.1 电力线信道的数学模型
基本的电力线信道模型如图1所示,该模型描述的电力线信道分为两个部分,分别是信道传输特性和噪声。电力线信道通常可以描述为线性系统,即用单位冲击响应或频率响应函数表示。可等效为信号通过一个线性滤波器。电力线信道中的噪声通常为加性噪声,等效为信号电压与噪声源电压之和,如式(1)所示。其中“⊗”表示卷积运算。


图1 基本电力线信道模型
1.2 硬件结构
系统的硬件结构如图2所示。为实现对具有双向通信功能的电力线设备的测试,仿真系统的每个端口都应该具有双向通信功能。使用定向耦合器实现对接收信号和对待测设备发送信号的隔离。FPGA控制放大器对输入信号进行放大以实现最大的动态范围,然后经过A/D采样转换为数字信号进行进一步处理。用于对信道进行仿真的滤波器参数预先存入FPGA中,该滤波器在每次仿真前进行修改,仿真过程中保持不变。信号经过虚拟的电力线信道后通过D/A再次转换为模拟信号。

图2 仿真系统的硬件结构图
FPGA中的噪声序列产生器用于产生各种电力线噪声。该噪声序列经过另一个D/A转换器形成模拟信号,该模拟信号通过受SNR控制单元控制的放大器进行输出,从而调节输出信号中噪声成分的功率。SNR参数同滤波器参数一样,在仿真前进行设定和修改。
2 电力线信道和噪声特性分析
2.1 电力线传输特性分析
电力线通信信道不同于其他有线通信信道,而类似于一个总线线路。信号通常不会从发射机沿一条路径径直地传到接收机,而是会传过一些附加的路径,或者是反射路径。一个最简单的分支模型,可以用来对电力线信道进行分析[1],如图3所示。信号从A点向C进行传输,在B点处由于阻抗不匹配将引起一部分信号的反射。B点的信号同时将分别向C点和D点传输。D点并非接收终端,因此也存在阻抗不匹配的情况,它将一部分信号反射回B点,并依次循环下去。复杂的电力线信道可以分解成该模型的并联或级联。

图3 电力线多径传输模型
根据 Manfred Zimmermann的研究[1],多径效应下的电力线信道可表示为
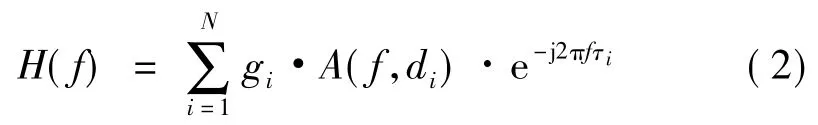
其中,A(f,di)为第i条路径的衰减,其与频率以及路径长度有关。τi为信号在第i条路径上的延时,其值由式(3)给出

式中,c0为真空中的光速;εr为导线的介电常数。
根据传输线理论,用于传输高频信号的电力线应该按照低损耗传输线进行分析,其特性阻抗Z0和传输常数γ分别用式(4)和式(5)定义
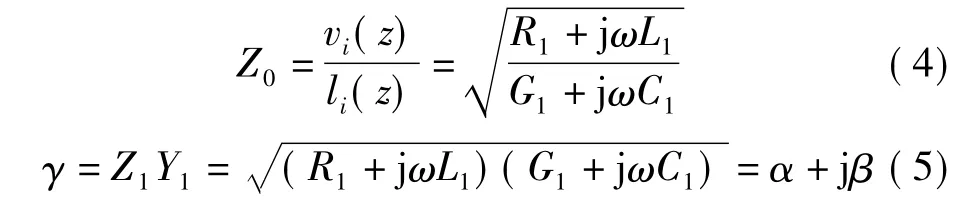
其中,α称为衰减常数,表示传输线上波行进单位长度幅值的变化;β称为相移常数,表示传输线上波行进单位长度的相位变化。单位长度内的分布式电阻R1是由趋肤效应引起,它和成一定的比例;单位线长度的内的分布式电导G1由耗散引起,它和f成一定的比例。因此,其传输常数可被简化为
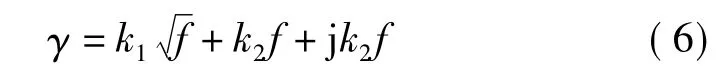
根据进一步的测量和研究结果,更逼近的衰减因子α(f)的等式为

其中,k为介于0和1之间的值,根据式(2)和式(7)可得
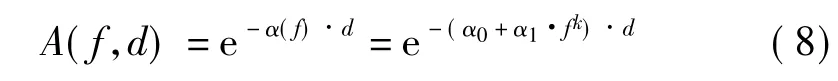
因此,电力线信道传输函数可被表示成

式(9)表示电力线传输特性的一般模型,其参数值可以根据测量得到,或者按传输线原理对电力线介质进一步分析得出估计[2]。在仿真分析中,可以通过调节该参数模型中多径的数N对该模型的精确度进行控制。
2.2 电力线噪声的分类
Manfred Zimmermann[3]将电力线噪声分为:
(1)有色背景噪声。这类噪声具有相对低的功率谱密度,并且功率随着频率的变化而变化。这类噪声由大量低功率噪声源叠加而成,其功率谱密度往往随时间变化,变化周期一般为几分钟到几个小时。
(2)窄带噪声。这类噪声常常由经过幅度调制的正弦信号产生,最常见的源是由无线电广播站的发射信号耦合到电力线上产生。
(3)与电网频率异步的周期脉冲噪声。这类噪声的频率一般为50 Hz~200 kHz之间,因此这类噪声具有离散的线谱,谱间隔即为噪声频率。该噪声通常由开关电源或其他用电器,如CRT显示器等造成。
(4)与电网频率同步的周期脉冲噪声。这类噪声的频率在我国一般为50 Hz或100 Hz。这类噪声持续时间很短,通常为μs级。它有随频率降低的频谱密度。这类噪声由供电电源通过整流二极管引起,因此与工频交流电同步。
(5)异步脉冲噪声。这类噪声是由于各种电子或者机械的开关瞬态造成。这类噪声通常随机出现,持续时间从μs到ms级不等。它的功率谱密度很大,最大比背景噪声高50 dB以上。
这5类噪声中,前3类的统计特性变化较慢,一般变化周期为数秒,数分钟甚至数小时,而功率谱通常较低,因此这几类噪声可以统称为背景噪声。而后两类噪声时变性很强,一般在μs和ms级。最关键的是,这两类噪声功率谱密度值通常很大,因此能造成比特错误甚至是突发连续错误。因此这两类噪声是电力线通信中需要被考虑和克服的主要难点。
Michael Bauer[4]对电力线的脉冲噪声进行了测量和仿真,提出脉冲噪声的时域特性可以用式(10)逼近,其结果如图4所示。

图4 电力线脉冲噪声
为便于分析,可以对上述电力线脉冲噪声进行简化。认为当上述脉冲的包络达到一定值时为一个脉冲的开始,下降到一定值后为该脉冲结束。简化的电力线脉冲噪声的特性可以用3个参数进行描述:脉冲幅度A,脉冲宽度tw和脉冲到达时间tarr。按照上述模型,文献[16]对时域特性进行了统计分析:脉冲噪声宽度tw一般为数十μs,幅度为数百mV,功率谱高出背景噪声约50 dB,在家用电力线环境中,脉冲噪声出现时间的比率约为0.00135%,平均出现频率为0.122次/s。
3 仿真算法的设计与实现
3.1 电力线信道的仿真
利用式(9)可以针对某一特定信道进行基于测量的建模。为使仿真结果不失一般性,根据实际电力线信道中大量存在的随机分布分支,可以假设冲击信号通过该信道将随机在不同时刻产生不同幅值的信号在接收端进行叠加,根据中心极限定理,大量独立同分布的随机变量的和的分布服从高斯分布。因此,信道响应的包络服从瑞利分布。当信道中存在直射分量时,即电力线信道中的情况,随机变量服从均值不为零的高斯分布,此时,信道响应的包络服从莱斯分布。即

其中,A为主信号即直射信号的峰值;I0()是修正的0阶第一类贝塞尔函数。莱斯分布常用参数K来描述,K定义为确定信号的功率与多径分量方差之比。
在Matlab中,通过调用莱斯信道函数可以生成莱斯信道滤波器,使用该滤波器对信号进行处理可以模拟莱斯信道。莱斯信道的函数原型为
CHAN=RICIANCHAN(TS,FD,K,TAU,PDB)其中,TS为采样频率;FD为多谱勒频移;K为莱斯分布参数;TAU为各路径延时向量;PDB是相应路径的增益向量。
根据Han Kim的研究[27]多径时延的最大值一般<50 ms,Zimmermann[1]提供若干了由式(9)所描述的信道的多径分量gi的值。根据上述结果,考虑到仿真的复杂度,将多径数设为50条,多径时延向量用均值为25 ms,方差为2.5×10-6的正态随机变量生成;多径分量大小用均值为0.05,方差为0.05的正态随机变量生成。经过仿真,可得到莱斯信道的Matlab仿真结果如图5所示。
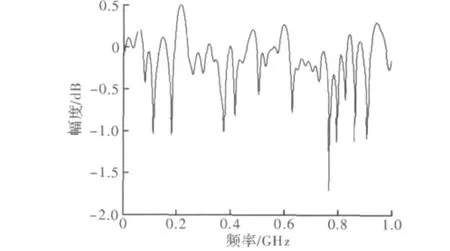
图5 50条多径信道的频谱图
3.2 电力线噪声的仿真
根据文中研究结果,电力线噪声主要可分为5大类,其中有色背景噪声、窄带噪声和异步周期脉冲噪声由于其功率谱密度较小,统计特性相对恒定,而统一归为背景噪声。大量的背景噪声的和可以使用高斯白噪声进行模拟。
同步周期脉冲噪声的周期为10 ms或20 ms,与G3-PLC系统一个数据帧的持续时间相当,因此在一帧数据内只会出现极少的同步周期脉冲,为简化处理,可以将它并入突发脉冲噪声。Manfred Zimmermann[5]提出采用马尔科夫过程对突发脉冲噪声的出现进行模拟,根据研究结果,该模型能较精确的模拟脉冲噪声的出现时间,但该模型由于运算量大而带来实现上的困难。一种较简单且不失精确性的方法是根据突发脉冲出现的时间、时间宽度等参数的统计特性,由式(10)进行模拟。
文中脉冲噪声出现时间的比率约为0.00135%,平均出现频率为0.122次/s。假设系统采用fs的采样频率,则每个采样点出现脉冲噪声的概率为Pimp=0.122/fs;脉冲噪声平均宽度为wimp=1.35×10-5×fs/0.122个采样点。不妨定义在脉冲噪声包络幅度下降到最大值的5%以内时为脉冲噪声的结束时刻。将上述参数代入式(10)可得

根据上述参数的推导结果,可以在Matlab中通过如下方法模拟电力线噪声:
用随机数产生函数Randsrc产生一个N维[0,1]分布的随机向量作为脉冲噪声标示向量,其中P(x=1)=pimp;然后循环搜索标示向量,当该点的值为1时,自该点起调用脉冲发生函数;再用脉冲发生函数首先产生两个正态分布的独立的随机数A0、B0,并产生一个正态分布的随机变量d,其均值由式(11)求得。最后按式(10)产生一个输出向量,并将其加到结果向量中。
通过上述方法产生的电力线脉冲噪声如图6所示。
由于噪声出现的概率较低,因此在仿真时需要延长仿真时间,而这样会导致过大的数据量,因此在此次仿真中,调低了采样频率,但这并不影响仿真效果。从图中可以直观地看出,该结果与电力线实际的噪声环境比较吻合。
3.3 仿真算法的实现
信道的特性在单次仿真中应该保持不变,可以借助PC机对信道进行设计。按文中讨论的算法求出信道的单位冲击响应向量,并通过RS232口或者网口等方法发送给仿真系统,在FPGA中采用FIR滤波器实现该单位冲击响应。同时为实现带反馈回路的信道的仿真,可以在FPGA中实现另一路并行的IIR滤波器,通过PC机的参数对两路滤波器的输出进行切换。噪声的仿真方法在PC机上产生相应的参数传入FPGA,为保证更好地实时性,也可以在FPGA中采用伪随机序列产生电路实现。
4 结束语
针对电力线信道和噪声的标准实时仿真平台,对于电力线通信设备的开发和测试是必要的,它能帮助开发人员在设备研发的每一步对可靠性进行快速测试,并且针对不同电力线通信产品提供统一的测试定标平台。文中在对电力线信道特性和噪声进行深入分析的基础上,提出了一种电力线信道实时仿真平台的设计方法,该算法使用Matlab仿真验证了可行性。该平台可使用基于FPGA的硬件实现,具有较高的实用价值。
[1]MANFRED Z,KLAUS D.A multipath model for the powerline channel[J].IEEE Transactions on Communications,2002,50(4):553 -559.
[2]MENG H,CHEN S,GUANY L,et al.Modeling of transfer characteristics for the broadband power line communication channel[J].IEEE Transactions on Communications Delivery,2004(7):1057 -1064.
[3]MANFRED Z,KLAUS D A.Modeling of impulsive noise in broad - band powerline communications[J].IEEE Transactions on Electromagnetic Compatibility,2002,44(1):249 -258.
[4]MICHAEL B,LIU Wenqing,KLAUS D.Channel emulation of low -speed PLC transmission channels[C].IEEE International Symposium on Power Line Communications and Its Applications(ISPLC 2009),2009:267 -272.
[5]MANFRED Z,KLAUS D.An analysis of the broadband noise scenario in powerline networks[D].Taipei:Institute of Computer& Communication,2005.

