考虑可中断负荷及风电随机性的电网短期经济调度

陈 明 童小娇，2 蒙万兴

（1.长沙理工大学电气与信息工程学院；长沙 410114；2.衡阳师范学院，湖南 衡阳 421002）

近年来，随着可再生能源技术的日益成熟，新能源在电力系统中的应用得到了大力的发展，并成为世界各国在发展智能电网时必须考虑的因素之一。风能作为一种可被有效转化为电能的清洁绿色能源，是目前技术最成熟的可再生能源发电方式[1]。但风力发电受风速的影响，具有很强的随机性和间歇性，而且大型风电场的并网运行会对系统的稳定性、可靠性以及整个电力系统供需平衡都将产生影响。在当前电力市场环境下，负荷相当于一种有功备用，若出现紧急情况，尤其是电力系统处于用电高峰期，各发电机组处于其出力边际状态时，系统调度员可通过经济手段动员可中断负荷，快速降低负荷水平，达到新的电力平衡点，以避免事故的扩大[2-3]，可见可中断负荷的加入对于解决短时电力不平衡能够起到良好的作用，同时体现了负荷的市场参与性。因此，探讨风电随机性对电力系统稳定性的影响以及可中断负荷在电力系统经济调度中的运用是很有意义的。

在以往的文献中，已有不少涉及可中断负荷的研究，文献[2]提出一种解决短时电力缺额的方法—秒级可中断负荷，并对其在不同情况下的差异进行研究。文献[3]给出可中断负荷的最优合同购买模型，以购买费用最小作为目标函数。文献[4]使用条件风险价值作为风险度量工具，建立同时考虑地低电价可中断负荷合同和高补偿可中断负荷合同的供电商决策模型。但以上这些文献均没有考虑可中断负荷对电力系统稳定性以及在调度中的经济性的影响。在经济调度方面，文献[5]采用一种改进的粒子群优化算法来求解含风电场的电力系统动态经济调度问题。其模型是利用正负旋转备用来应对风电功率预测误差给系统调度带来的影响，其在短期经济调度中不太实用。文献[6]提出输电元件负载率，分析不同调度方式下对输电能力使用的影响规律，然而并未涉及能源发电和负荷随机性所带来的影响。

为了克服以往调度方式中存在的不足，以及更好的度量输电线路负载水平、本文综合考虑输电线测误差等因素，建立了含风电场的电网短期经济调度模型。采用经济学领域已得到广泛应用的CVaR理论来刻画输电线路安全性，从而将线路安全性与风电随机性联系起来。同时，将可中断负荷作为预测误差的填补，从而提高系统运行的经济性和安全性。

1 CVaR理论

设f( x, y)为损失函数。其中， x∈R，y∈Rm为随机变量，x表示的是一些随机性的因素(如风电出力等)。y的概率密度函数为p(y)，对于确定的x，由y引起的损失 f ( x, y)是R上服从某一分布的随机变量，其不超过临界值a的分布函数为

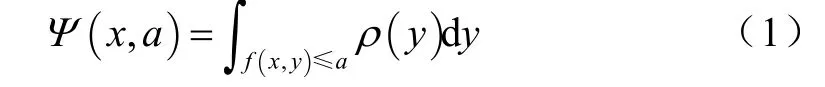
对于任意固定的x，Ψ( x, a)作为a的函数是决策变量x下的损失累积分布函数。Rockafeller和Uryasev证明了它对a非减且右连续[7]。将置信水平用β表示，αβ(x)表示决策变量为x时损失f( x, y)所对应的VaR值，其计算公式为

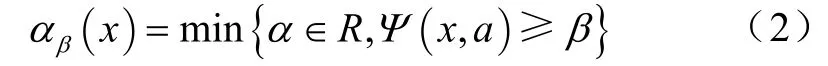
又以 φβ(x)表示损失f( x, y)不小于αβ(x)时的CVaR值

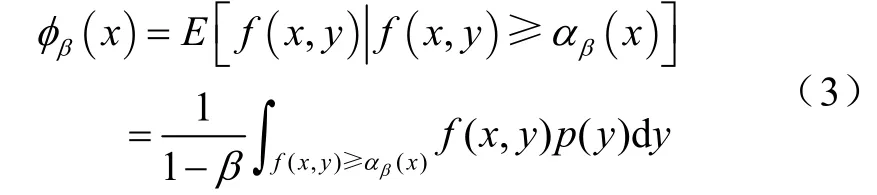
由于式中含有VaR函数 αβ(x)项，而αβ(x)的解析表达式难以求出，所以文献[7]引入一个相对简单的函数 Fβ( x,α)代替 φβ(x)计算CVaR

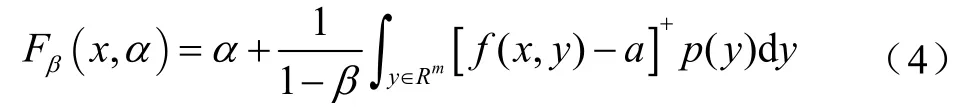
通常情况下，概率密度函数 p ( y)的解析表达式难以得到，可以利用随机变量y的历史数据，或者使用蒙特卡罗法[8]模拟样本数据来给出上式中积分的估计。设 y1, y2,· ·,yq为y的q个样本， 则函数的估计值为

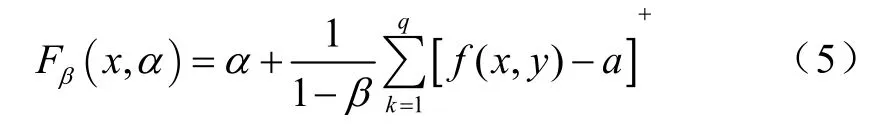
因此在实际计算中，通常基于式（5）来计算相应的CVaR和VaR值。

2 风机的功率特性

风电机组发出的有功功率主要取决于风速的大小。目前，国内外对风速分布曾有不少的研究，在一年当中的大部分时间里风速是比较平缓的，风速在0～25m/s之间的概率很高，绝大多数地区的年平均风速分布都可以用 Weibull分布函数来描述。但如果研究的时间段比较短，也可以假设风速v近似服从正态分布[9-10]。

本文在此研究的是短期经济调度，因此采用正态分布作为风电有功出力的模拟较为合适；其概率密度函数为

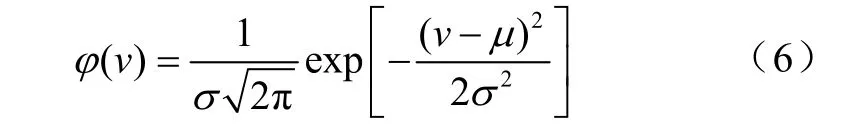
式中，μ为平均风速，σ2为方差。

3 预测误差以及可中断负荷的处理

3.1 预测误差

与传统系统的调度相比，当风电并入系统后，影响调度的不确定因素除了负荷，还有由于风速波动所引起的不确定的风电有功输出。因此本文在考虑负荷预测误差的同时，还考虑了风电出力预测误差以提高调度的精确性。已知预测负荷为为负荷预测误差，则实际负荷D可以表示为和ΔD之和，ΔD为服从均值为0、方差为的正态分布的随机变量[11]，即

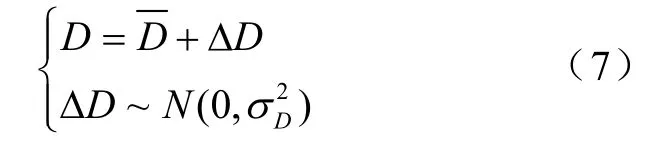
根据文献[12-13]的研究，σD其标准差可由下式求得

式中，k一般取值为1。

风电预测同样存在偏差， PW为实际风电出力；为预测风电出力；ΔPW为风电预测偏差，该偏差为服从均值为 0、方差为的正态分布的随机变量。

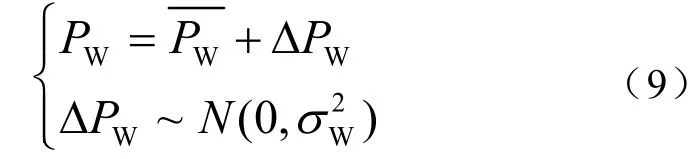
上式中σW可由下式求得

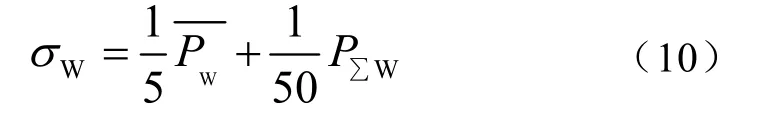
式中， PΣW为风电的总装机容量。

全网预测总用电误差为： Δ DA=ΔD - ΔPW，ΔDA全网总误差服从均值为0，方差为σ2的正态分布，则

3.2 可中断负荷

在实际运行中，由于负荷预测偏差或者发电机故障等原因，系统可能会出现容量缺额的情况。电网公司通过签订可中断负荷合同，在系统存在容量缺额时，不仅可以通过平衡市场中再购入部分容量，而且可以中断负荷减少容量需求来调节，这将大大减少在波动性较大的平衡市场购电的风险[14]。本文考虑的是短期经济调度，因此，要在较短的时间内进行备用的调用，尤其是在电厂装机容量存在缺额的地区，存在一定难度。这就需要考虑通过削减负荷来达到电网的稳定运行。本文将预测误差所带来的容量缺额由削减可中断负荷来填补，但削减供应容量将会给用户造成损失。这时，供电公司就需要根据可中断负荷合同，给予这部分用户一定的补偿，补偿函数[15]如下：

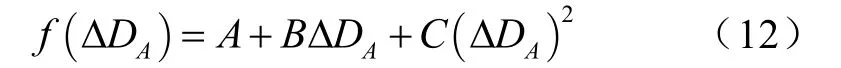
式中， f （ΔDA）为因中断用户负荷给予用户的损失补偿，A，B，C为补偿系数。当 Δ DA≥ 0 时，表示负荷预测值偏低导致供不应求，尚需中断一部分负荷，以使得全网平衡。 Δ DA＜ 0 时，则供大于求，不需要给予可中断负荷用户赔偿。因此，在此只需考虑 Δ DA≥ 0 的情况。

4 经济调度模型

4.1 常规机组成本特性函数

在不考虑风电的运行费用时，基于原有的开停机状态，常规机组的发电费用[16]：

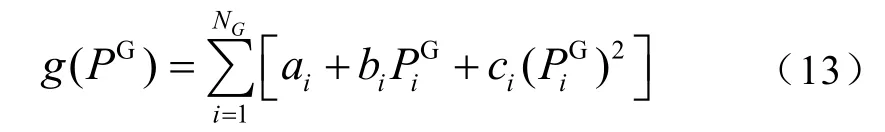
式中， g ( PG)为发电成本函数。NG是常规发电机组的数目，是常规机组功率输出成本常数。

4.2 约束条件

1）机组出力上下限约束

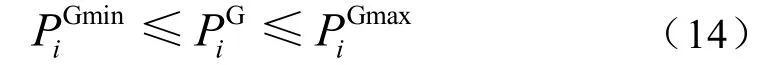
分别为机组的输出功率的上下限。

2）电量平衡约束

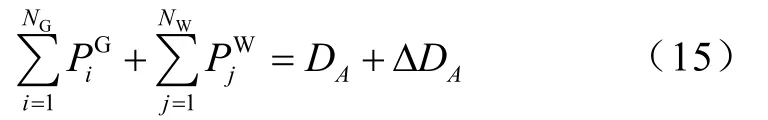
式中，NW为风电机组总数，DA为需求侧负荷预测值，本文对系统的有功网损忽略不计。

3）节点功率平衡约束

每条线路的负载率为

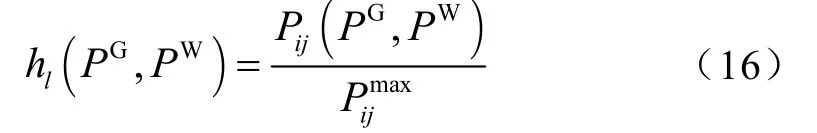
在直流模式下，满足

其中，Xij为线路i-j的电抗，δi是节点i的电压的相角。则系统应满足直流潮流方程：

B’是n-1维方阵，P是节点注入功率向量，δ为节点相角矩阵。其中 DA是负荷预测量，从上式可以解得，

4）基于CVaR的线路约束

为方便起见，对于复杂的网络，只要寻找到负载率 h ( PG, PW)最大的那条支路，则系统的风险限制函数 φ (PG, PW)为

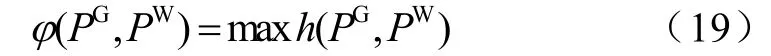
该支路的最大风险函数值小于给定风险阀值，系统运行则是满足要求的。

假设，风险程度不超过最大安全阀值a的概率为

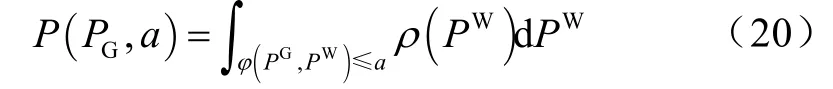
则在置信水平α下的CVaR为

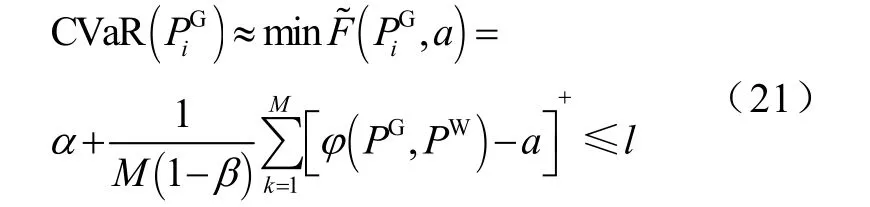
4.3 调度模型

设 l为风险值的约束，其满足 l ∈[lmin, lmax]，令则考虑输电线路安全约束及可中断负荷的含风电场电力系统短期经济调度模型为

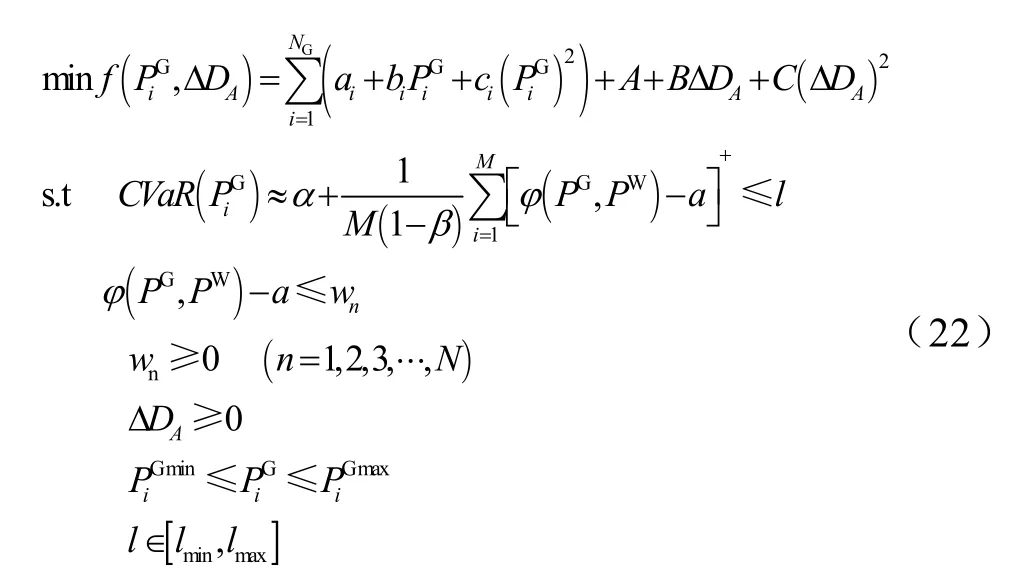
5 算例分析

5.1 仿真系统

以标准IEEE14节点系统对模型进行理论分析。节点1为平衡节点，表1为常规机组相关特性数据，表2为对可中断负荷的补偿参数。系统总负荷预测值为7.2p.u，额定容量为600kW的风电机组从节点10接入系统。风电预测误差为均值为0，方差为152，负荷预测误差为均值为 0方差为 252的正态分布，功率基值为100MVA。

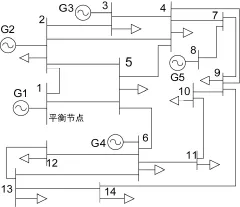
图1 14节点系统

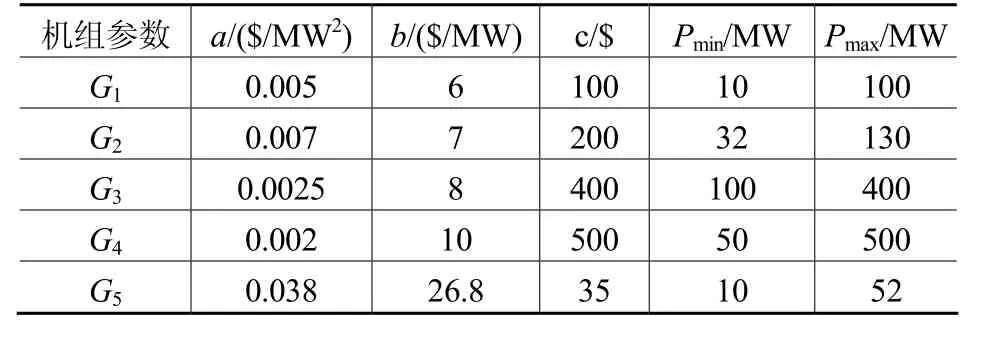
表1 机组参数

表2 对可中断负荷的补偿

5.2 计算结果分析

结合考虑线路传输功率及模拟系统，给定l∈[-0. 0265,-0.058]，利用潮流计算软件算出每条支路的功率分布情况，找到支路负载风险度最大的那条支路，最后利用Matlab编写程序，调用fmincon语句，得出调度模型的最优解。

1）不同置信水平的比较

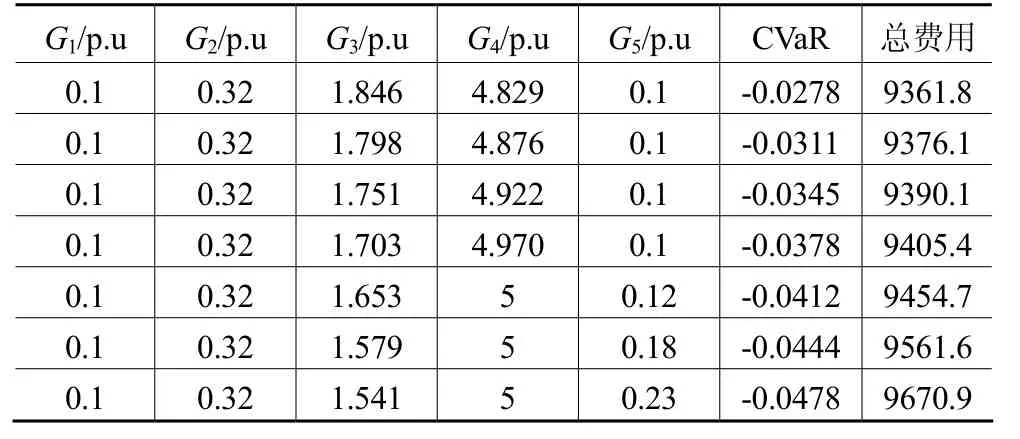
表3 置信水平为85%时

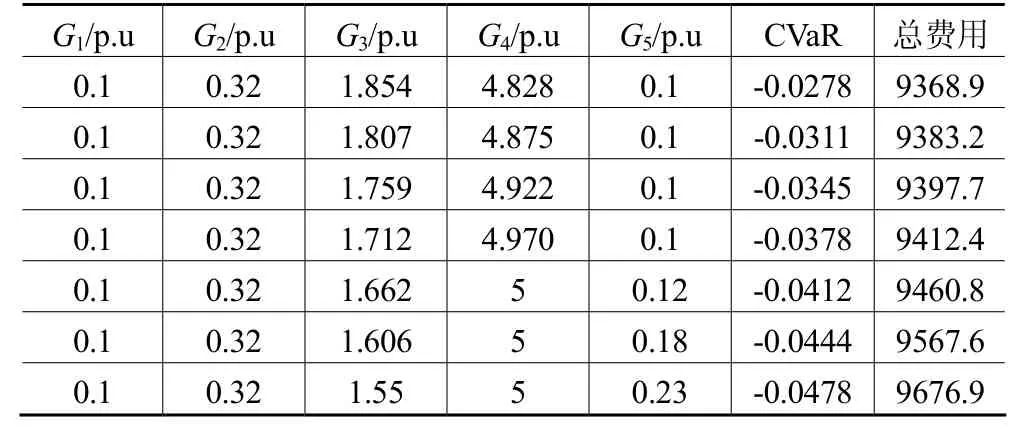
表4 置信水平为95%时

通过比较表3和表4可知，置信水平α越高，系统对风险越是规避。为了提高系统的可靠性，经济性就需要作出一定的让步。当α趋向于100%的时，负载风险度最大的那条支路，不能超过最大传输功率极限。

2）预测总误差对系统运行费用的影响

将置信水平设为 95%，CVaR=-0.058，风电预测值为0.00168 p.u，负荷预测值为0.02955 p.u，对不同的预测误差ΔDA时的目标函数总费用进行比较，如表5所示。

通过表5中的比较可知，预测总误差ΔDA越大，需要给予用户的补偿费用越高，目标函数总费用也越高。因此，提高预测的精度能有效降低目标函数的总费用。

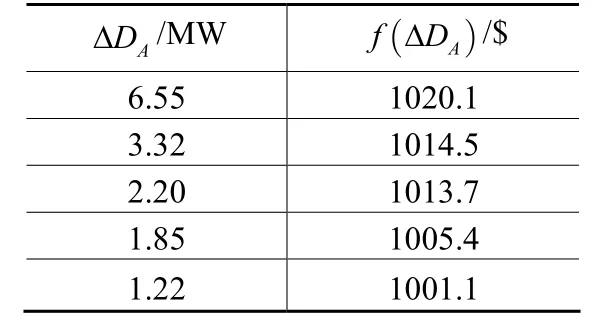
表5 预测总误差的影响

6 结论

本文建立了不同于以往的短期经济调度模型。以基于CVaR的输电支路负载率作为模型的风险约束，同时充分考虑可中断负荷及负荷、风电预测误差，并将可中断负荷作为储备来填补系统的总误差。该模型的目标函数不仅考虑常规机组的发电费用，还将可中断负荷用户的补偿费用包括在内。最后通过14节点系统计算分析，证明了该模型的有效性。随着智能电网的发展，新能源发电、需求响应计划的不断加入，该模型将能很好的适应新的电网运行环境，为解决在智能电网条件下电力系统的安全经济运行提供保障。

[1]朱凌志,陈宁,王伟.兼顾接入地区无功需求的风电场无功控制策略[J]. 电力系统自动化, 2009, 33(5): 80-85.

[2]都亮,刘俊勇,田立峰,杨可.电力市场环境下秒级可中断负荷研究[J].中国电机工程学报，2008,28(16):90-95.

[3]王建学,王锡凡,王秀丽.电力市场可中断负荷合同模型研究[J]. 中国电机工程学报, 2005, 25 (9): 11-16.

[4]江岳文,陈冲,温步瀛.基于随机模拟粒子群算法的含风电场电力系统经济调度[J].电工电能新技术,2007,22(3):85-89.

[5]姜文,严正.基于一种改进粒子群算法的含风电场电力系统动态经济调度[J].电力系统保护与控制, 2010,38(21):174-183.

[6]张强,韩学山,徐建政.安全经济调度与均匀调度间关系分析[J].电力系统及其自动化学报,2005,17(2):84-89.

[7]R.T.Rockafellar, S.Uryasev. Optimization of conditional value-at-risk, The Journal of Risk, 2000,2(3):21-41.

[8]乔瑞·菲利普.VaR:风险价值—金融风险管理新标准.张海鱼.译.北京:中信出版社,2000.

[9]雷亚洲,王伟胜,印永华.风电对电力系统运行价值分析[J].电网技术, 2006,26(5):10-14.

[10]Bowden G J, Barker P R, Shestopal V O,et al.The weibull distribution function and wind power statistics[J].Wind Engineering,1983(7):85-98.

[11]王乐,余志伟,文福栓.基于机会约束的最优旋转备用容量确定[J].电网技术,2006,30(20):14-19.

[12]Bunn D W. Forecasting load and prices in competitive power markets[J].Proc. IEEE，2000，88(2)：163-169.

[13]谭伦农,张保会. 市场环境下的事故备用容量[J].中国电机工程学报,2002,22(11):54-58.

[14]王建学,王锡凡,王秀丽.电力市场可中断负荷合同模型研究[J].中国电机工程学报,2005,25(9):11-16.

[15]葛炬, 张粒子.可中断负荷参与的备用市场帕累托优化模型[J]. 电力系统自动化,2006,30(9):34-37.

[16]查浩,韩学山,王勇.电力系统安全经济协调的概率调度理论研究[J].中国电机工程学报,2009,29(13):16-22.