随时间任意变化荷载下砂井地基固结分析
郭彪,韩颖,龚晓南,卢萌盟
(1. 重庆市市政设计研究院,重庆,400020;2. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州,310058;3. 机械工业第三设计研究院,重庆,400039;4. 中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州,221008)
砂井联合堆载预压是提高软土地基承载力、减小地基沉降的有效方法,对常荷载下砂井地基的固结问题,国内外众多学者进行了大量的研究,取得了丰富的成果[1-16]。但在实际工程中,地基荷载通常是随时间变化的,对于变荷载下的砂井地基固结问题,也有不少研究者进行了研究,如:Olson[16]假设砂井为理想井,给出了荷载分级线性施加情况下的解析解;Tang等[17-18]进一步考虑了涂抹和井阻作用;Zhu等[19]用数值方法对砂井地基进行了研究,并考虑了大变形、非线性等因素的影响;耿雪玉等[20]运用 Laplace变换求得了复杂荷载作用下未打穿砂井地基的固结解。上述解答要么考虑的因素不够全面,要么过于复杂,很难应用于工程实践。另外,大量的研究[12-14]表明:涂抹区土体由于受到的施工扰动程度不同,其渗透性是连续变化的,离砂井越近,扰动程度越高,土的渗透性越小。为此,本文作者考虑涂抹效应、井阻作用、地基土横竖向组合渗流等因素,并且涂抹区的水平渗透系数采用更符合实际的线性连续变化模式,将上部荷载通过傅里叶变换转化为三角级数的形式[21],得到更便于工程应用的分析变荷载下砂井地基固结的解析解,并编制了应用程序。
1 固结方程及求解
图1所示为随时间任意变化荷载下砂井地基示意图。在推导过程中,进行以下假定:
① 等应变条件成立;
② 土中水的渗流服从Darcy定律;
③ 荷载在地基中引起的附加应力沿深度均匀分布;
④ 在任一深度 z处从土体流入桩体的水量等于桩体中向上水流的增量。
根据等应变条件,有:
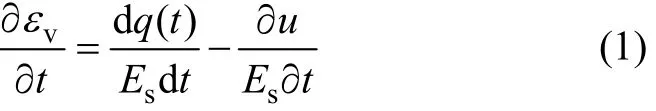
式中:εv为地基竖向应变;Es为土体压缩模量;q(t)为上部荷载;u为土体任一深度处的平均超静孔压,
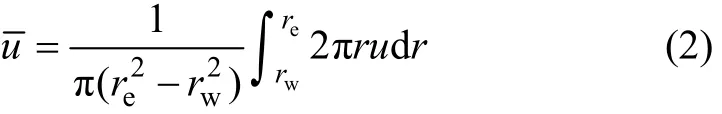
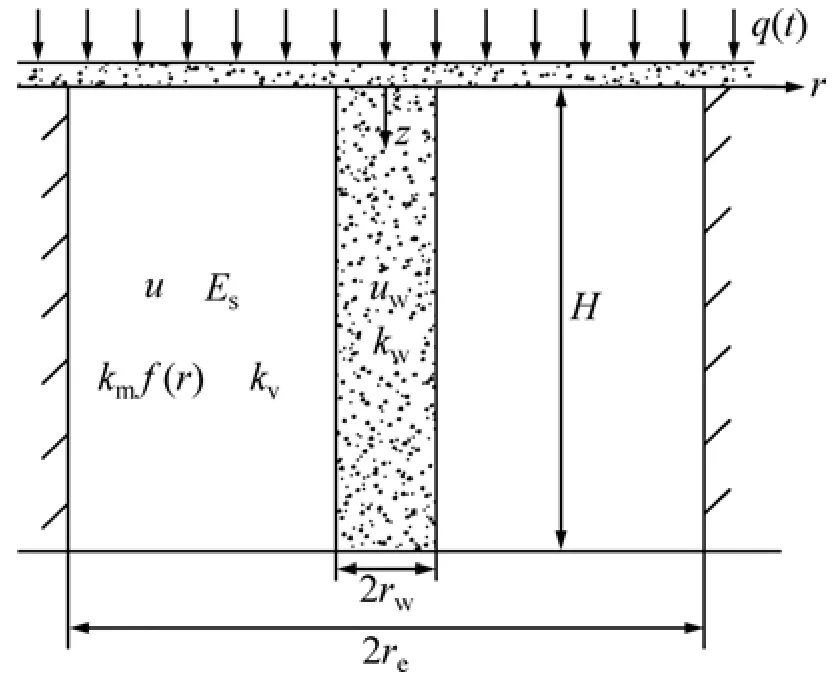
图1 随时间任意变化荷载下砂井地基简化模型Fig.1 Model for consolidation of soft soil with vertical drains and general time-dependent loading
rw为砂井半径;re为砂井影响区半径;u为土体任一点的超静孔压。
根据谢康和等[9]的研究,砂井地基的固结方程为:

式中:kv为土体竖向渗透系数;kw为砂井渗透系数;kmf(r)为土体水平向渗透系数;km为最大水平渗透系数;f(r)为描述渗透系数随r变化的函数。桩周流量连续方程为:
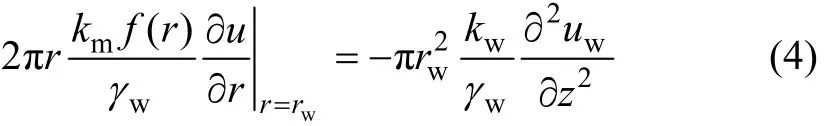
式中:uw为砂井任一深度处的超静孔压。边界条件为:

任何加载都需要一个过程,即使是瞬时加载也是如此,只不过时间很短。因此,初始条件可写为:
⑤ t=0时,u=0。
[10,17],可以得到固结控制方程为:
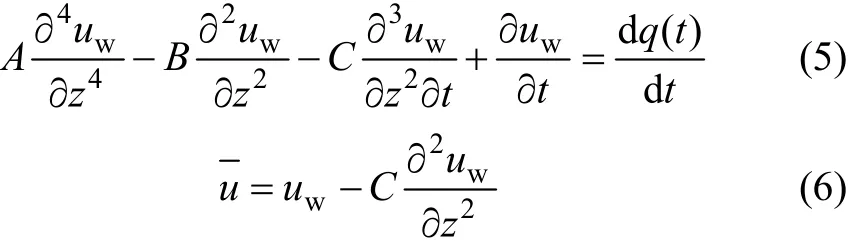
式中:

假设地基土体涂抹区水平渗透系数随r增大而线性增大,未扰动区保持不变,不妨称其为模式 1,如图2(a)所示。参考文献[10],可以得到:

其中:


图2 影响区土体水平渗透系数Fig.2 Horizontal permeability coefficient in influence zone
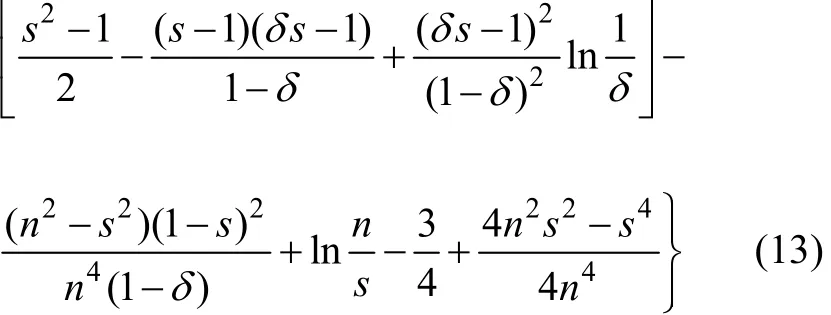
s=rs/rw;rs为涂抹区半径;δ为最小渗透系数和最大渗透系数之比,0<δ=kn/km<1。
为了便于比较分析,本文也给出涂抹区水平渗透系数不变情况下(模式2)的解,如图2(b)所示。此时,Fa的表达式为:

方程(5)是非齐次微分方程,其边界条件式③和④以及初始条件式⑤是齐次的,满足冲量定理条件,可设:
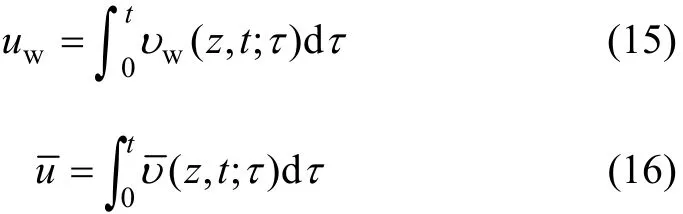
由式(6),υ和υ满足关系式:
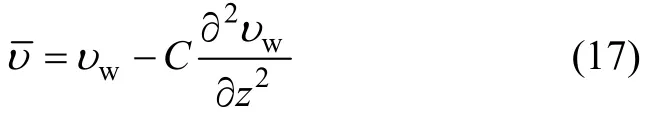
其中,wυ方程(5)对应齐次微分方程的解:
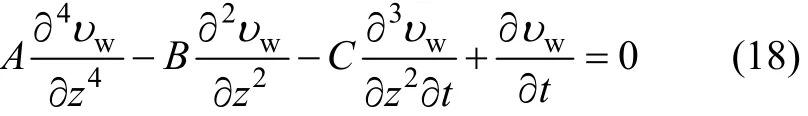
边界条件和初始条件为:
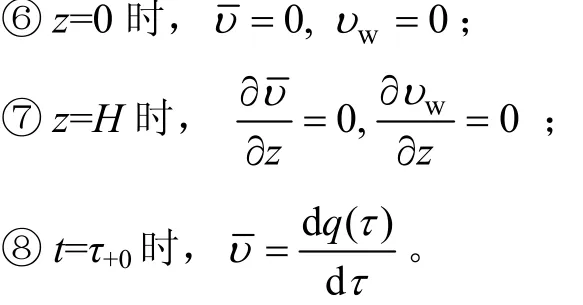
采用分离变量法求解,设
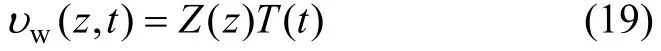
代入式(18)可得:
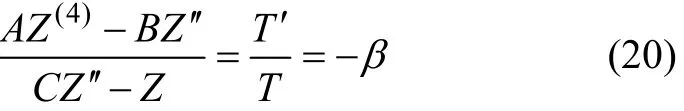
即

利用边界条件⑥和⑦以及式(17)和(19),可得:
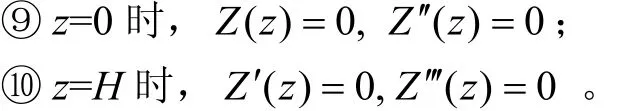
常微分方程(21)的特征方程为:
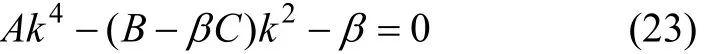
其解可表示为:
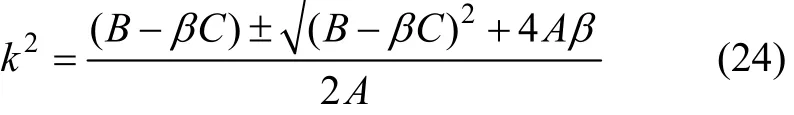
式(21)的通解可表示为:
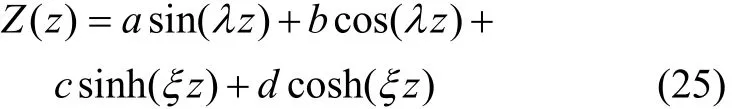
由边界条件⑧和⑨可得:

则 Z ( z) = asin(λ z)。由z=H和Z′(z)=0可得:

将k=λi代入式(23),可得:
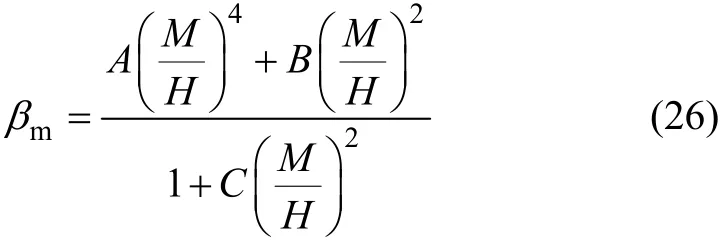
方程(22)的通解可表示为:

由于其初始时刻为t=τ+0,可设 T (τ+0)= Δ ,Δ 为1个常数,则:

方程(18)的解可写成:
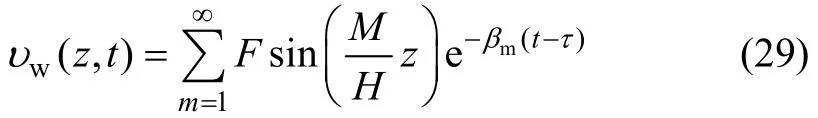
将式(29)代入式(17)可得:
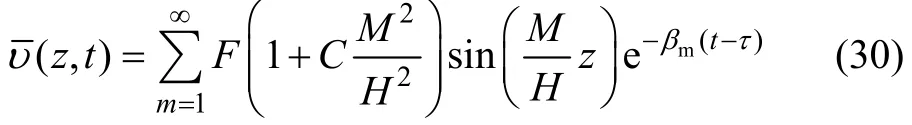
根据三角函数的正交性和初始条件⑧可得:
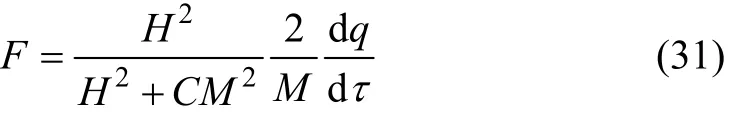
将式(29)和(30)分别代入式(15)和(16)可得固结方程的解为:
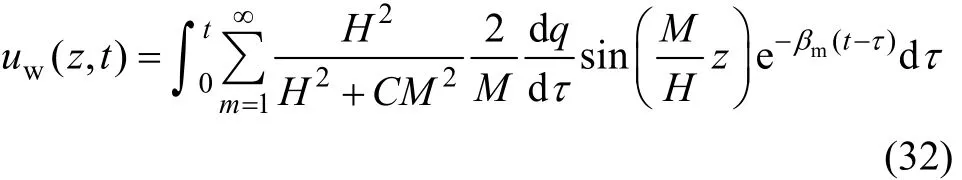
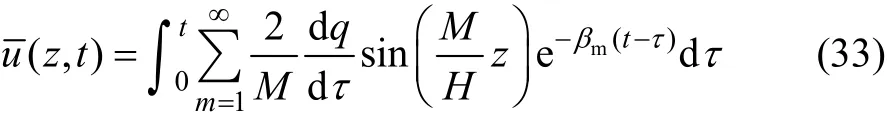
在 q(t)比较复杂的情况下,上面的解难以应用,为方便工程应用,需要将其简化。对荷载 q(t),一般来说是满足狄利克雷(Dirichlet)条件的,可将其展开成傅里叶级数:
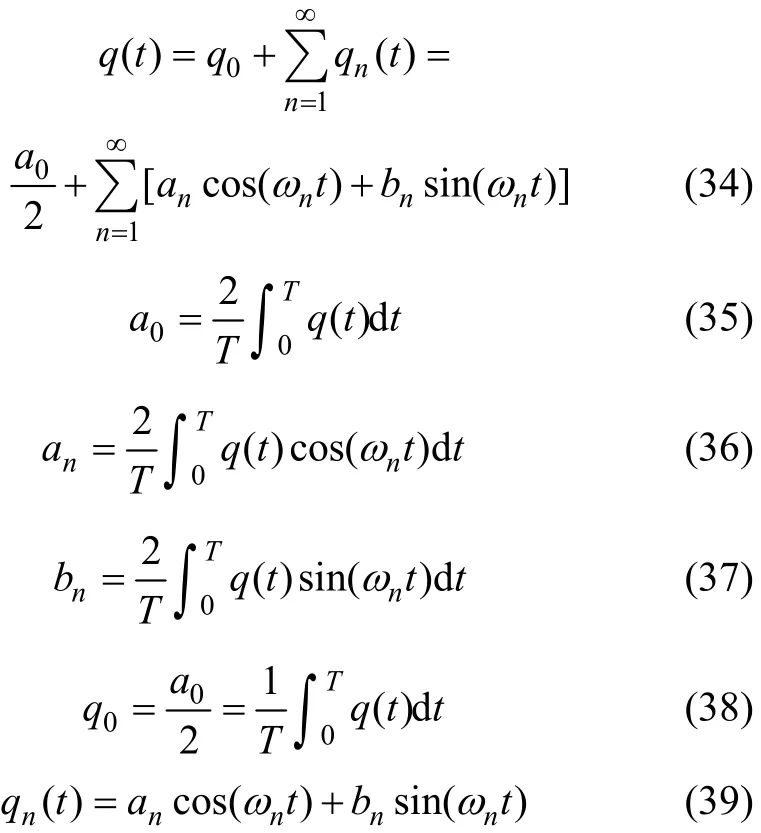
式中:ωn= 2 n π/ T;T为q(t)的周期。在q0的作用下,dq0=dt=0,因此,对地基孔压没有影响。
在变载qn(t)作用下,将式(39)代入式(32)和(33)并积分可以得到:
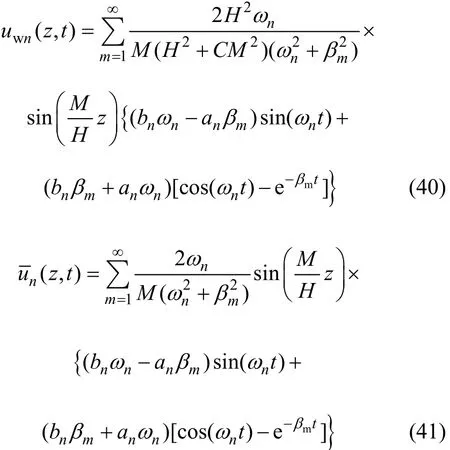
运用叠加原理,地基在荷载 q(t)作用下,砂井和地基土的平均超静孔压可写成:
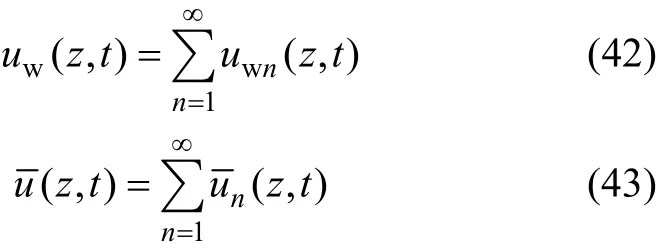
求得了u( z, t)后,可以得到地基任意深处的固结度为:
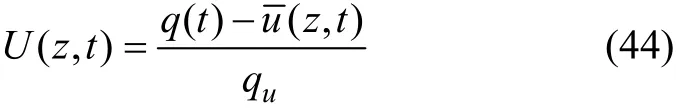
式中:qu为最大荷载。
进一步可以得到地基的总平均估计度为:
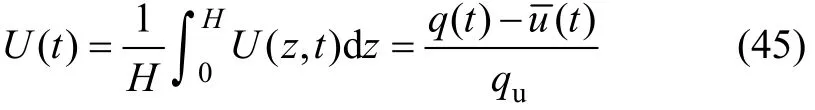
式中:

2 an和bn的求解
系数an和bn的求得是上述求解过程中的关键。在分级线性施加荷载情况下(如图 3所示),对其中任意一级加载,q(t)可写为:

将式(47)代入式(36)和(37)可以得到:
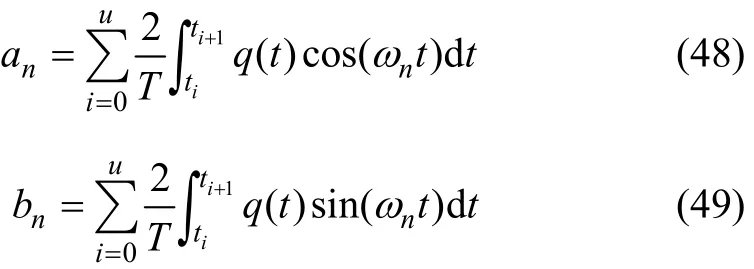
其中:
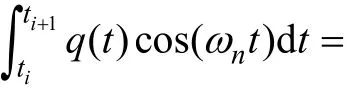
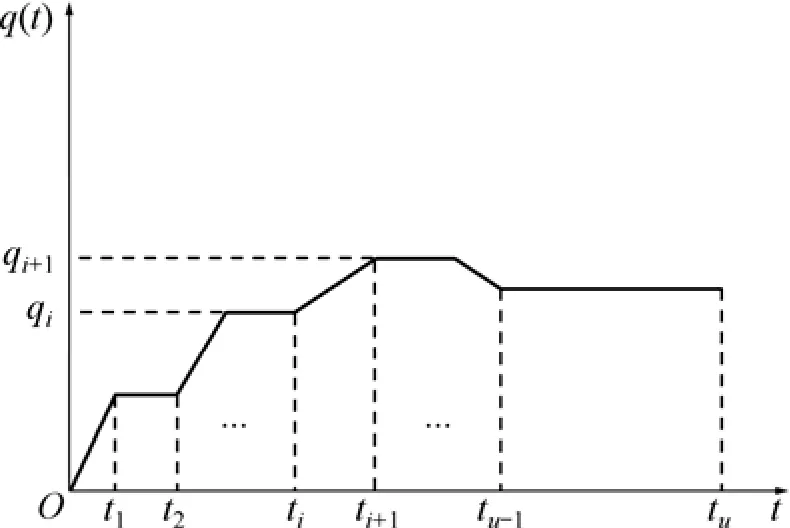
图3 分级线性施加荷载示意图Fig.3 Loading process consisting of a combination of linear and constant functions with time
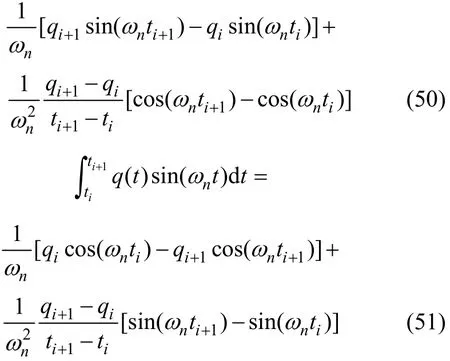
在荷载随时间曲线变化的情况下,可以用直线段来模拟,如图4所示。当直线段足够多时,就可以达到足够工程应用的精度要求。这样,可以同样采用式(48)~(51)求得 an和 bn。
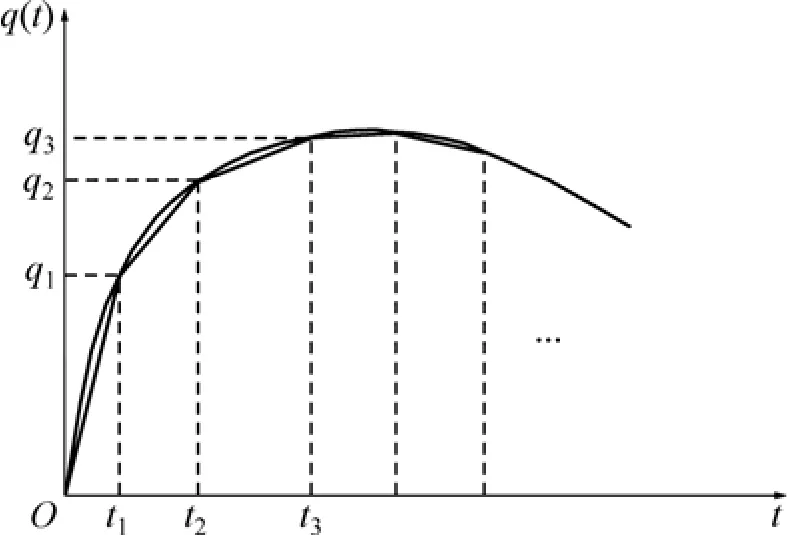
图4 荷载随时间曲线变化示意图Fig.4 Relationship between loading and time
3 程序的编制
利用计算机编程,上面的求解过程很容易实现。步骤如下。
(1) 输入地基土参数和砂井参数,包括:砂井半径rw,影响区半径re,涂抹区半径rs,土层厚度H,砂井渗透系数kw,土体竖向渗透系数kv,未扰动土水平渗透系数km,扰动程序参数δ,土体压缩模量Es等。
(2) 输入上部荷载参数,若q(t)由如图3所示的一系列直线段组合而成,则输入各拐点处的时间ti和qi;若荷载为如图4所示的随时间曲线变化,则根据需要取一系列t,再由荷载函数q(t)计算对应的q,时间间隔越小,精度便越高;输入q(t)的周期T,若q(t)不是周期函数,则可将最大分析时间取作T。
(3) 由式(26)求得 βm。
(4) 利用式(48),(49)和(50)求得一组系数 an和 bn。
(5) 利用式(40)和(41)求得在荷载qn(t)作用下砂井和地基土的超静孔压
(6) 递增 n,重复步骤(4)和(5),将其结果叠加求得在荷载 q(t)作用下砂井和地基土的超静孔压 uw(z,t)和u( z, t)。
(7) 利用式(45)求得地基的平均固结度。
4 解的验证
设荷载单级线性施加,如图5所示。图6所示为本文解与唐晓武解[17]的比较结果。由于唐晓武解假设涂抹区水平渗透系数不变,为了使两者条件一致,本例解中采用式(14)表达的Fa,即模式2。
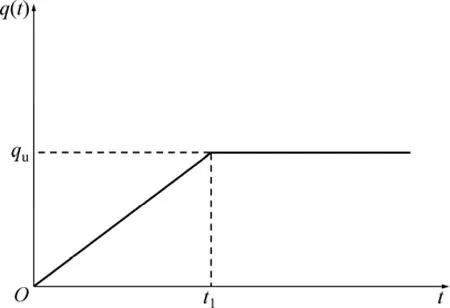
图5 单级线性施加荷载Fig.5 Single ramp loading
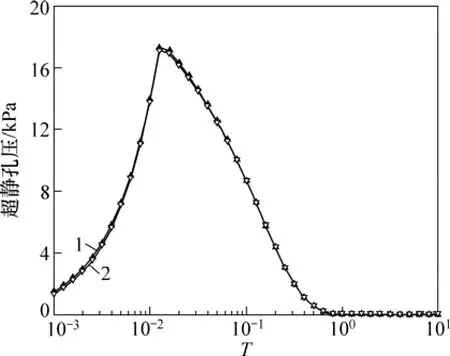
图6 本文解与唐晓武解的比较Fig.6 Comparison of the present solution with that by Tang X W
由图6可见:2孔压曲线基本上重合,由此可知本文解是可靠的。计算参数为:wr=0.2 m,re=4 m,rs=2 m,H=20 m,kw=1×10-3cm/s,km=kv=1×10-6cm/s,δ=0.5,Es=20 MPa,达到最大荷载时间t1=30 d,最终荷载qu=20 kN。
5 几种荷载形式下的固结性状
5.1 多级线性施加荷载
荷载分级线性施加示意图如图7所示。其中,荷载分两级线性施加,t1=30 d,t2=60 d,t3=100 d,q1=20 kN,qu=50 kN。其他计算参数与上例的相同。2种渗透系数模式下超静孔压曲线及固结曲线如图8和图9所示。从图8和图9可以看出:考虑渗透系数呈线性变化时固结要快。

图7 荷载分级线性施加示意图Fig.7 Multi-ramp loading

图8 荷载两级线性施加时地基的超静孔压曲线Fig.8 Excess pore-water pressure of sand drains foundation under double-ramp loading
5.2 三角形循环荷载
三角形循环荷载如图 10所示,其中 T=60 d,qu=50 kPa,其他计算参数与前面的相同。地基超静孔压变化曲线如图11所示。从图11可以看出:超静孔压呈震荡减小趋势,震荡幅度并不随时间减小,但其震荡中线逐渐趋于一定值;在循环荷载作用下,当上部荷载减小即卸荷时,地基土回弹体积膨胀,从而产生负超静孔压。渗透系数为模式1时的孔压曲线在模式 2时孔压曲线的下方,即孔压为正时,模式 1的孔压小于模式2的孔压,但模式1的负孔压要比模式2的大。
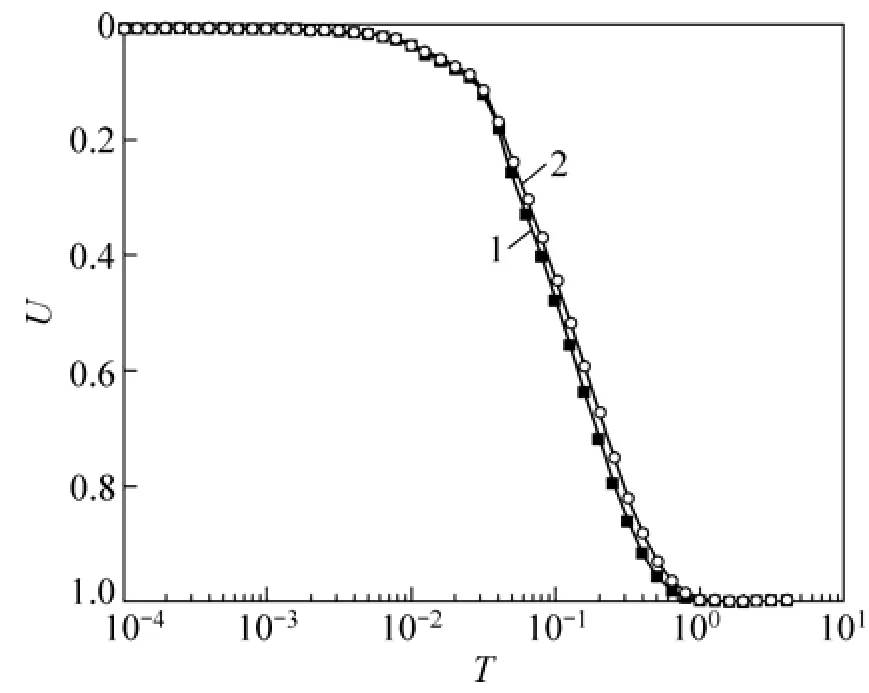
图9 荷载两级线性施加时地基的固结度曲线Fig.9 Consolidation rate of sand drains foundation under double-ramp loading

图10 三角形循环荷载Fig.10 Triangular cyclic loading
图 12所示为三角形循环荷载作用下地基有效应力曲线。从图12可以看出:有效应力呈震荡上升趋势,同样其震荡幅度不随时间减小,但其震荡中线逐渐趋于一定值。模式1的有效应力要比模式2的大。
5.3 梯形循环荷载
地基在如图 13所示的梯形循环荷载作用下,T=180 d,t1=30 d,t2=90 d,t3=120 d,qu=50 kPa,地基超静孔压曲线和附加有效应力曲线如图14和图15所示,可以看出其与三角形循环荷载作用时有相似的规律。
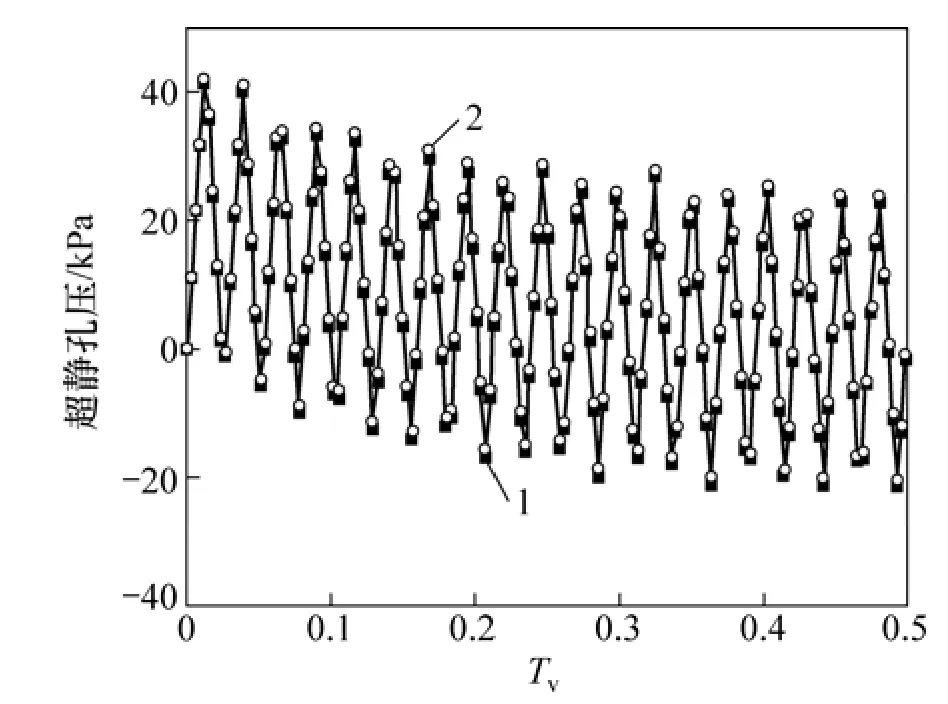
图11 三角形循环荷载作用下地基超静孔压曲线Fig.11 Excess pore-water pressure of sand drains foundation under triangular cyclic loading
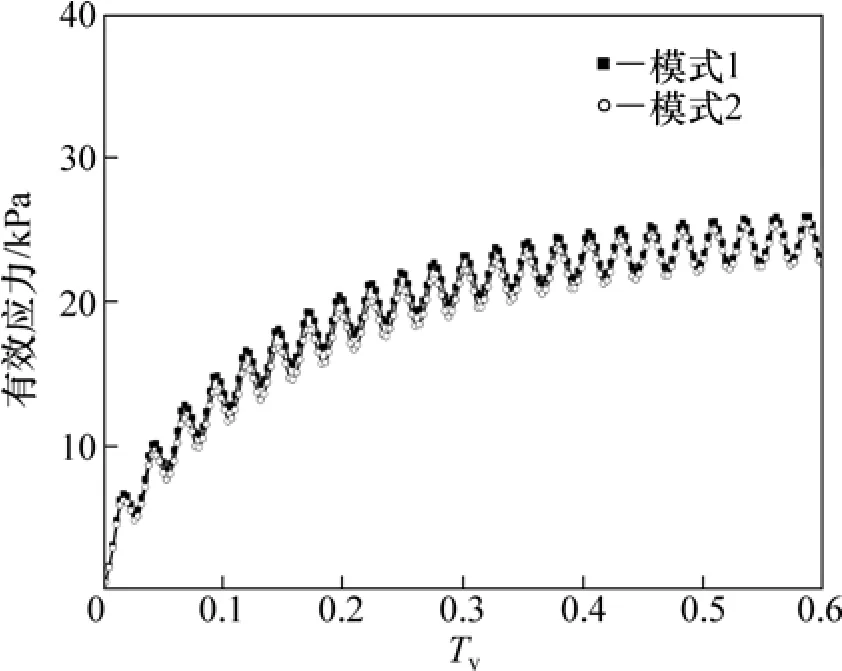
图12 三角形循环荷载作用下地基有效应力曲线Fig.12 Effective stress of sand drains foundation under triangular cyclic loading

图13 梯形循环荷载Fig.13 Trapezium cyclic loading
5.4 抛物线形循环荷载
如图16所示为二次抛物线形循环荷载,抛物线方程为:
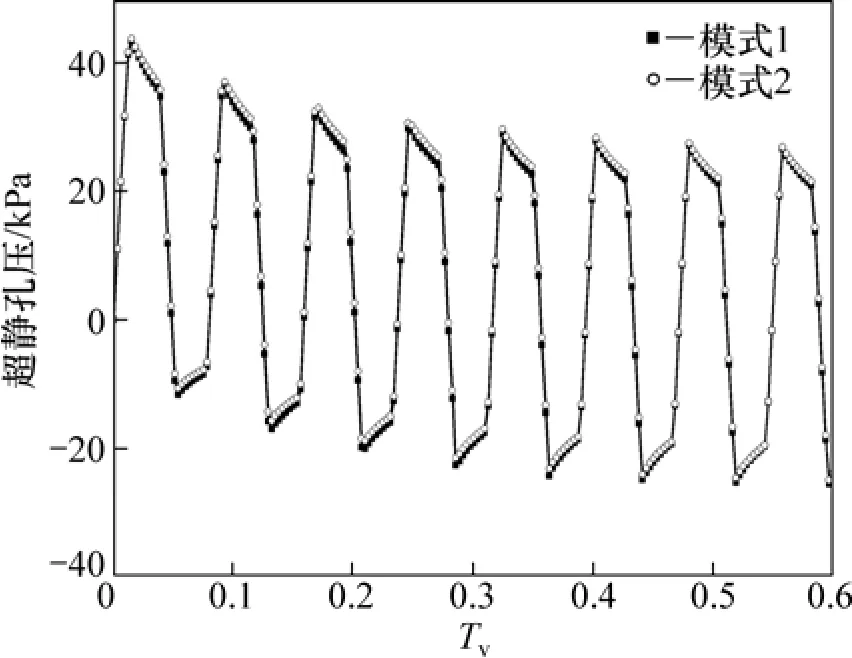
图14 梯形循环荷载下地基超静孔压曲线Fig.14 Excess pore-water pressure of sand drains foundation under trapezium cyclic loading
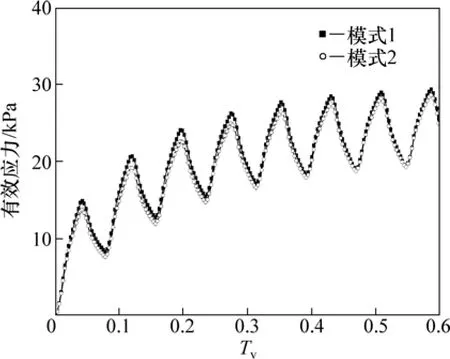
图15 梯形循环荷载下地基有效应力曲线Fig.15 Effective stress of sand drains foundation under trapezium cyclic loading
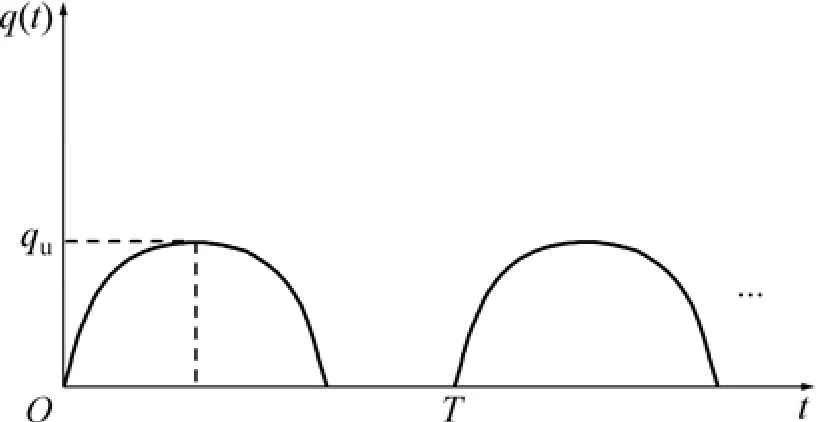
图16 抛物线形循环荷载Fig.16 Parabolic cyclic loading
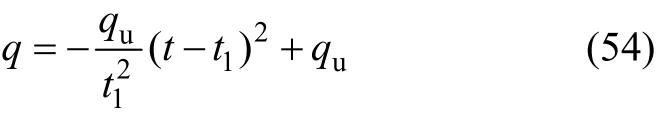
如t1=60 d,T=180 d,qu=50 kPa,在循环荷载作用下,考虑渗透系数呈线性变化。地基的超静孔压曲线和附加有效应力曲线如图17和图18所示。其中,X为逼近抛物线的直线段段数。
从图17和图18可以看出:它们均具有很好的收敛性,当X为2时4时有较大差别,X为4时与10时差别不大,而X为10时与为100时的孔压曲线和有效应力曲线基本上重合,这说明采用直线段模拟荷载随时间曲线变化是很有效的。

图17 抛物线形循环荷载下地基超静孔压曲线Fig.17 Excess pore-water pressure of sand drains foundation under parabolic cyclic loading
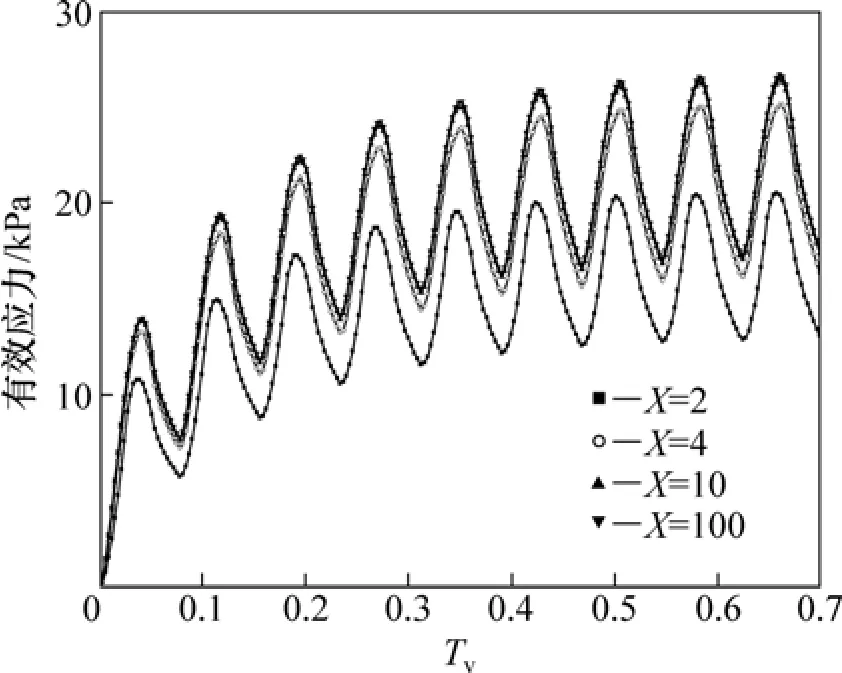
图18 抛物线形循环荷载下地基有效应力曲线Fig.18 Effective stress of sand drains foundation under parabolic cyclic loading
6 结论
(1) 在荷载分级施加时,考虑涂抹区渗透系数线性变化时地基固结速度比假设其不变时的快。
(2) 在循环荷载作用下,砂井地基超静孔压呈震荡减小趋势,在卸荷时可能会产生负压,震荡幅度并不随时间减小,但其震荡中线逐渐趋于一定值;考虑涂抹区渗透系数线性变化时的正孔压比假设其不变时的小,而负超静孔压更大。
(3) 在循环荷载作用下,地基有效应力呈震荡上升趋势;同样,其震荡幅度不随时间减小,震荡中线逐渐趋于一定值。考虑渗透系数线性变化时有效应力比假设其不变时的大。
(4) 当荷载随时间曲线变化时,采用多段直线段逼近荷载曲线是求解此问题的有效方法。
参考文献:
[1] Barron R A. Consolidation of fine grained soil by drains wells[J].Transactions of ASCE, 1948, 113: 718-742.
[2] Richart, Jr F E. A review of the theories for sand drains[J]. Proc ASCE, 1957, 83(S3): 1-38.
[3] Yoshikuni H, Nakanodo H. Consolidation of soils by vertical drain wells with finite permeability[J]. Soils and Foundations,1974, 14(2): 35-46.
[4] Hansbo S, Jamiolkowski M, Kok L. Consolidation by vertical drains[J]. Geotechnique, 1981, 31(1): 45-46.
[5] 曾国熙,王铁儒,顾尧章. 砂井地基的若干问题[J]. 岩土工程学报,1981, 3(3): 74-81.ZENG Guo-xi, WANG Tie-ru, GU Yao-zhang. Several problems of sand drains[J]. Chinese Journal of Geotechnical Engineering,1981, 3(3): 74-81.
[6] Hart E G, Kindner R L, Boyer W C. Analysis for partially penetrating sand drains[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1958, 84(S4): 1-15.
[7] 陈根媛. 多层地基的一维固结计算方法与砂井地基计算的改进建议[J ]. 水利水运科学研究, 1984, 5(2) :18-29.CHEN Gen-yuan. One-dimensional consolidation of layered systems and a suggestion for improving calculation of sand-drained subsoil[J]. Journal of Nanjing Hydraulic Research Institute, 1984, 5(2): 18-29.
[8] 谢康和. 砂井地基: 固结理论、数值分析与优化设计[D]. 杭州: 浙江大学建筑工程学院, 1987: 1-62.XIE Kang-he. Sand drained ground: Analytical & numerical solutions of consolidation and optimal design[D]. Hangzhou:Zhejiang University. College of Civil Engineering and Architecture, 1987: 1-62.
[9] 谢康和, 周开茂. 未打穿竖向排水井地基固结理论[J]. 岩土工程学报, 2006, 28(6): 679-684.XIE Kang-he, ZHOU Kai-mao. Consolidation theory for soft soil with partially penetrated vertical drains[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 679-684.
[10] 卢萌盟, 谢康和, 张玉国, 等. 考虑土体水平渗透系数变化的复合地基固结解[J]. 浙江大学学报: 工学版, 2008, 41(11):1996-2001.LU Meng-meng, XIE Kang-he, ZHANG Yu-guo, et al.Analytical solution for consolidation of composite foundation accounting for variation of soil horizontal permeability coefficient[J]. Journal of Zhejiang University: Engineering Science, 2008, 41(11): 1996-2001.
[11] Tang X W, Onitsuka K. Consolidation of double- layered ground with vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25: 449-465.
[12] Bergado D T, Asakami H, Alfaro M C, et al. Smear effects of vertical drains on soft Bangkok clay[J]. Journal of Geotechnical Engineering, 1991, 117(10): 1509-1530.
[13] Indraratna B, Redana I W. Babaoratory determination of smear zone due to vertical drain installation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(2): 180-184.
[14] Sharma J S, Xiao D. Characterization of a smear zone around vertical drains by large-scale laboratory tests[J]. Canadian Geotechnical Journal, 2000, 37(6): 1265-1271.
[15] XIE Kang-he, LU Meng-meng, LIU Gan-bin. Equal strain consolidation for stone columns reinforced foundation[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(15): 1721-1735.
[16] Olson R E. Consolidation under time dependent loading[J].Journal of the Geotechnical Engineering Division, 1977,103(GT1): 55-60.
[17] Tang X W, Onitsuka K. Consolidation by vertical drains under time-dependent loading. International[J]. Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9):739-751.
[18] Leo C J. Equal strain consolidation by vertical drains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004,130(3): 316-327.
[19] Zhu G F, Yin J H. Finite element analysis of consolidation of soils with vertical drain[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(4):337-366.
[20] 耿雪玉, 蔡袁强, 徐长节. 复杂荷载作用下考虑下卧层三维渗流的未打穿竖井地基固结分析[J]. 岩土力学, 2008, 29(6):1521-1529.GENG Xue-yu, CAI Yuan-qiang, XU Chang-jie. Soil of consolidation with partially penetrated vertical drains under complicated loadings considering three-dimensional seepage in soil beneath vertical drain[J]. Rock and Soil Mechanics, 2008,29(6): 1521-1529.
[21] Conte E, Troncone A. Radial consolidation with vertical drains and general time-dependent loading[J]. Canadian Geotechnical Journal, 2009, 46(1): 25-36.

