对称协同开采人工矿柱失稳的突变理论分析

陈庆发，古德生，周科平，苏家红

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；2. 广西大学 资源与冶金学院，广西 南宁，530004；3. 广西华锡集团股份有限公司，广西 柳州，545006)

随着全球对矿产资源的争夺进一步升级，原本不太引人注意的采空区隐患资源也日益受到关注。据不完全统计，这部分资源目前已经占我国有色金属资源的1/3，将成为我国矿业发展的重要接替资源[1]。传统观念认为资源开采与空区治理一种矛盾，分别独立设计、施工。本文作者从矿山大系统角度出发，以采矿环境再造理论[2-3]为指导，引入协同论，提出了“隐患资源开采与采空区处理协同”的矿业发展新技术模式及“协同利用”采空区处理新方法[4]。人工矿柱支撑顶板是采空区协同利用的基本模式之一，其与顶板之间的变形协调机制与矿石矿柱的相比有明显差别，研究人工矿柱的稳定性对于采空区周边隐患资源的协同开采起着至关重要的作用。对矿柱的稳定性分析，已从单一的强度理论、经验公式，向围岩组成的力学平衡系统的失稳研究方向发展。秦四清等[5-6]应用突变理论分析了对称开采时的矿柱失稳效应；李江腾等[7-8]对与非对称开采的矿柱失稳的突变模型进行探讨。本文作者基于突变理论，探讨对称协同开采时人工矿柱突发失稳的力学机理。

1 顶板-人工矿柱的协同作用模型及变形协调机制

人工矿柱形成前，顶板已经发生一定程度的下沉，在未发生突发失稳前，实施人工矿柱支撑措施，一方面，可抑制顶板后期下沉，避免可能的灾害事故；另一方面，留设的部分空间可作为资源开采过程中的部分空间进行利用(如爆破补偿空间)，实现隐患资源开采与空区处理的协同。

人工矿柱的空间表现形式有很多种，其中长条形人工矿柱最常见。根据材料力学，为简化分析，可将空区顶板视为弹性梁。为了达到最佳抑止效果，人工矿柱应布设于空区中间，荷载通过顶梁传递给人工矿柱。由于矿柱相对狭窄，单位长度的矿柱的作用视为作用在梁跨中的集中力 F，岩梁自重和上覆岩层的作用简化为均布载荷 q。在顶板未发生突发失稳前，对于硬岩来说，人工矿柱的变形远大于采空区周边围岩的变形，故认为梁是固支的。

根据前述分析，分别绘出采空区顶板-人工矿柱组合结构示意图及采空区顶板-人工矿柱协同作用力学模型[9-10]分别见图1和图2。

图1 顶板-人工矿柱组合结构Fig.1 Composite structure of roof-artificial pillar

图2 顶板-人工矿柱协同作用力学模型Fig.2 Synergistic effect mechanical model of roof-artificial pillar

根据损伤力学，人工矿柱的应力和应变关系可用weibull分布模型表达为[11]：

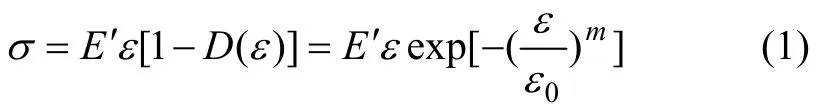
式中：σ和E′分布为人工矿柱胶结充填体的应力与弹性模量；ε0为平均应变测度；m为分布函数的形状参数，其物理意义反映了介质的均质性，定义为介质的均匀性系数。

对于上述协同作用力学模型，若梁和人工矿柱长度方向取1个单位，则宽度为d、高度为h的人工矿柱在被压缩量为u′时，有：

根据材料力学理论，无集中力F作用时，弹性梁达到图2虚线所示的静平衡位置，此时，考虑人工矿柱集中力F作用时，弹性量的部分能量释放在人工矿柱上，顶板弹性梁AO的弯距方程有：

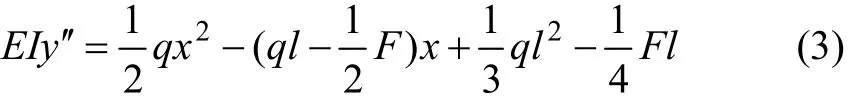
根据边界条件：

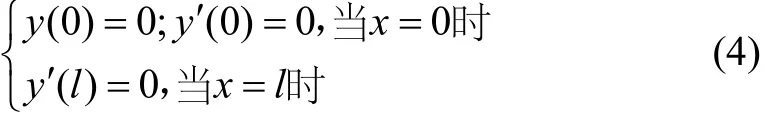
对式(3)积分，可得AO段的挠曲线方程：

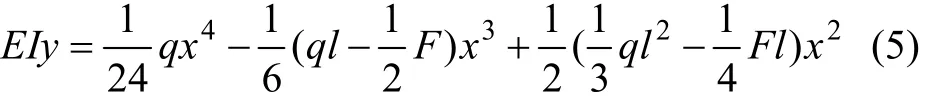
当x=l时，将y(l)=u0-u′代入挠曲线方程，可以得出人工矿柱压缩量关系式：

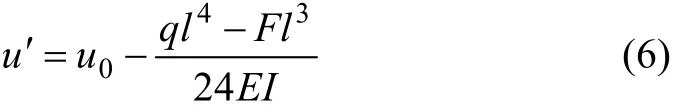
可见：人工矿柱压缩量是1个依赖于顶板弹性模量、泊松比、覆岩和顶板自重、顶板惯性距、采空区宽度、胶结充填体隔墙的弹性模量、宽度和高度等参数有关的量。

2 人工矿柱失稳的尖点突变模型

2.1 突变理论

1972年Thom创立并系统阐述了突变理论[12]，之后许多学者对该理论进行了研究，其中最有影响的是Zeeman提出的“突变理论”[13]。

突变理论认为，系统所处的状态可以用一组参数描述。当系统稳定时，标志该状态的某一函数就有唯一的取值。当参数在某一范围变化时，该函数有多个极值，系统处于不稳定状态。随着参数的继续变化，系统又从不稳定态进入另一稳定态，此时，系统就会发生突变。可以在不知道系统有哪些微分方程且不需求解微分方程的条件下，仅在几个假设的基础上，用少数几个控制变量便可以定性或定量地预测系统的性质。

由分类定理对梯度系统进行分类后指出：在控制变量不大于4个时，有7种初等突变形式(折叠、尖点、燕尾、蝴蝶、双曲点、椭圆脐点和抛物脐点)。目前，除个别情况，大多数研究者将问题归结为尖点突变模型去处理，如：施泽进等[14]建立了断层活动的尖点突变模型；黄润秋[15]建立了反倾斜坡弯曲拉裂的尖点突变模型；刘军等[16]通过综合考虑了地下水的影响建立了一个新的岩体失稳尖点突变模型。

2.2 人工矿柱失稳的尖点突变模型

尖点突变模型势能函数标准形式为：

式中：x为状态变量；u和v为控制变量。

相空间由状态变量x及控制变量u和v构成的三维空间。相空间平衡曲面 M 方程可通过对势能函数V(x)求导得到：

相空间中的图形称为突变流形，它是1个有褶皱的曲面，从而在不同的区域内，平衡位置为 1个、2个或3个。对应于中叶的势函数取极大值，平衡位置是不稳定的；而对应于上下叶的平衡位置上是稳定的。显然，在曲面有竖直切线，即满足：

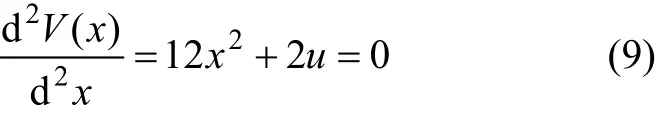
由式(9)可见：平衡位置的数目是不同的，这些点称为突变点或奇异点，实际上是曲线的拐点，是1条抛物线，如图3所示。

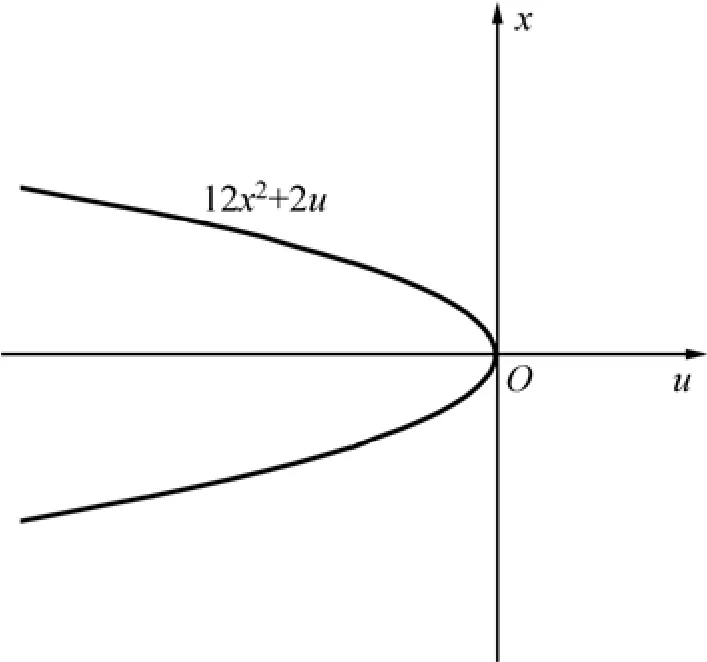
图3 势函数二阶导数为零的抛物线Fig.3 Parabolic at potential function’s second derivative zero

由式(8)和(9)消去x，可得到满足分支点集的方程：

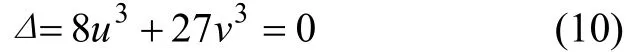
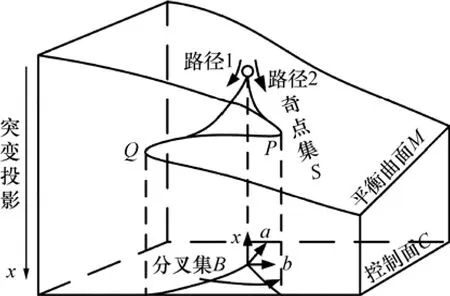
图4 尖点突变模型图Fig.4 Cusp catastrophe model diagram

平衡状态曲面由上、中、下3叶组成，如图4所示。从正面看，其形态似1条S形曲线，存在明显的拐点。设想系统的状态是以(x，u，v)为坐标的三维相空间的1点来表示，任一相点必然落在三叶曲面上。当系统参数发生变化时，它经历的平衡位置是突变流形上的1条曲线，这样，就可以分析由1个光滑的势函数所控制的系统中如何会出现不连续的性态。

由式(2)和(10)，根据静力平衡条件，可以得到总势能的一阶导数，即有突变流形方程：

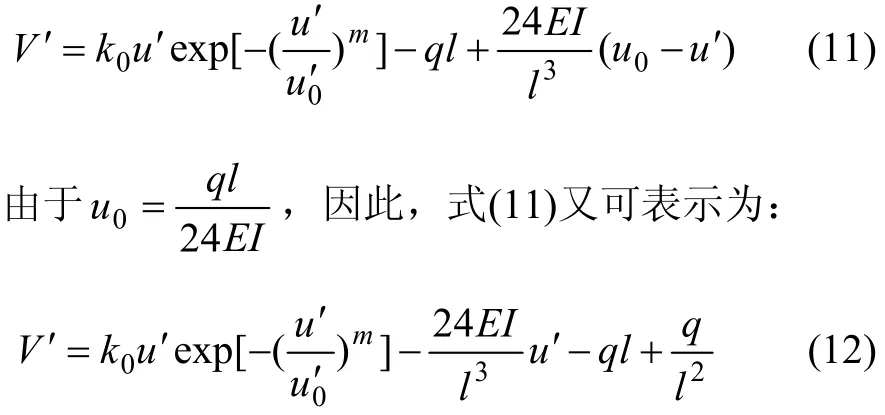
根据平衡曲面的光滑性质，求得尖点。尖点处有V″=0，得到：

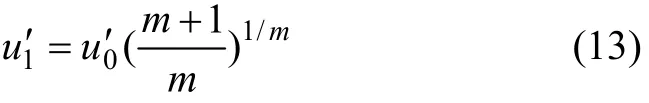
即尖点处在人工矿柱本构关系曲线拐点处。

将平衡曲面方程相对于1u′用Tayloy展开式展开，截取至3次项，然后，修改为尖点突变模型的平衡曲面标准形式4x3+2ux+v=0得：

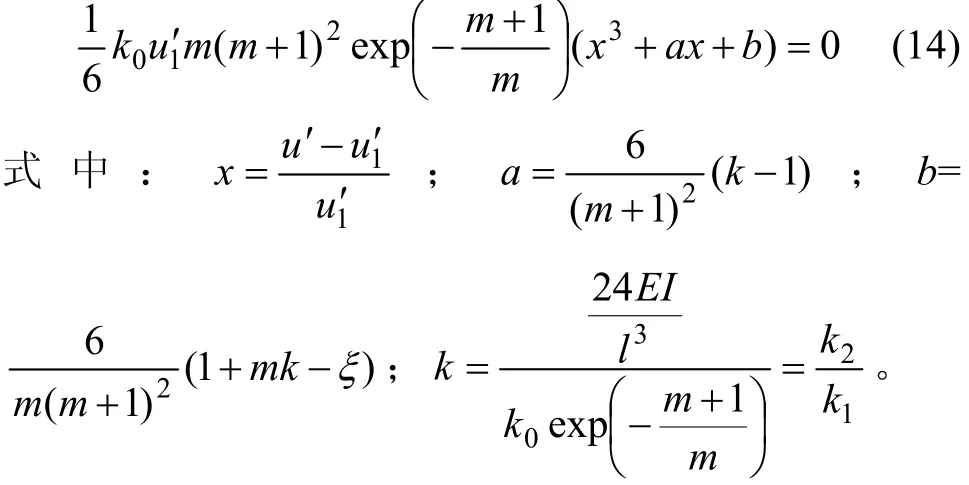
按尖点突变模型逐步进行推导，最终得到系统发生失稳的充要条件：

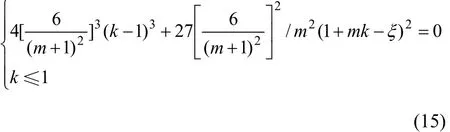
可见：系统突发失稳与系统刚度比有密切相关性；当系统的各部分的弹性模量、采空区宽度和人工矿柱的几何参数和力学性质参数等没有发生变化时，k随m的增大而减小。

3 人工矿柱对顶板稳定性调控作用

在m不变时，人工矿柱充填体的力学参数和几何参数是可以根据需要进行调控的，即的。

充填体的弹性模量E′可通过改变混凝土各项配比在一定范围内实现调整，必要时可能采用化学药剂进行调整。

在m和混凝土质量已确定的情况下(即E′确定)，人工矿柱的高度h对应于采空区的高度，加大矿柱宽度来强化其支撑能力，从而强化顶板的稳定性。

根据刚度比小于等于1的特性，施工中，人工矿柱的宽度必须满足如下公式：

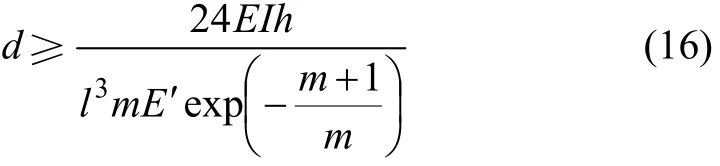
实施人工矿柱后的采空区剩余空间宽度，可根据采矿工艺对各种空间的要求进行留设，一般来说，爆破补偿空间不低于2 m，各种机械设备用硐室按规程而定(一般大于2 m)。

此外，采空区在人工矿柱有最小必要宽度后，无需形成更宽的人工矿柱，必要时可在剩余空间内通过充填采场废石进一步强化人工矿柱的支撑能力，调整采空区局地应力环境。

4 结论

(1) 通过分析实施人工矿柱工艺前后顶板力学状态的变化规律，建立了顶板-人工矿柱协同作用力学模型，分析了组合结构变形协调机制，推导了人工矿柱的压缩量表达式。

(2) 基于突变理论，建立了人工矿柱突发失稳的尖点突变模型。人工矿柱突发失稳与刚度比 k、介质均匀性系数m具有密切相关性。

(3) 通过改变人工矿柱的力学参数和几何参数，可在一定程度上调控顶板的稳定性和采空区局地应力环境，为协同开采隐患资源服务。

[1] 邹国良. 我国有色金属危机矿山发展对策[J]. 金属矿山, 2007,36(12): 22-23.ZOU Guo-liang. Countermeasures for development of China’s non-ferrous metallic mines in crisis[J]. Metal Mine, 2007, 36(12):22-23.

[2] 古德生, 李夕兵. 现代金属矿床开采科学技术[M]. 北京: 冶金工业出版社, 2006: 66-86.GU De-sheng, LI Xi-bing. Modern mining science and technology for metal mineral resources[M].Beijing:Metallurgical Industry Press, 2006: 66-86.

[3] 周科平, 高峰, 古德生. 采矿环境再造与矿业发展新思路[J].中国矿业, 2007, 16(4): 34-36.ZHOU Ke-ping, GAO Feng, GU De-sheng. Mining environment regenerating and new thoughts on the development of mining industry[J]. China Mining Magazine, 2007, 16(4): 34-36.

[4] 陈庆发, 周科平, 胡建华, 等. 碎裂矿段开采与空区处理协同研究[J]. 中南大学学报: 自然科学版, 2010, 41(2): 728-735.CHEN Qing-fa, ZHOU Ke-ping, HU Jian-hua, et al. Synergism study of mining and goaf treatment in cataclastic ore section[J].Journal of Central South University: Science and Technology,2010, 41(2): 728-735.

[5] 秦四清, 何怀锋. 狭窄煤柱冲击地压的突变理论分析[J]. 水文地质与工程地质, 1995, 18(5): 17-20.QIN Si-qing, HE Huai-feng. Analysis of the destabilization for the narrow coal pillar burst by the catastrophe theory[J].Hydrogeology and Engineering Geology, 1995, 18(5): 17-20.

[6] 徐曾和, 徐小荷, 唐春安. 坚硬顶板下煤柱岩爆的尖点突变理论分析[J]. 煤炭学报, 1995, 20(5): 485-491.XU Zeng-he, XU Xiao-he, TANG Chun-an. Theoretical analysis of a cusp catastrophe bump of a coal pillar under hard rocks[J].Journal of China Coal Society, 1995, 20(5): 485-491.

[7] 李江腾, 曹平. 非对称开采时矿柱失稳的尖点突变模型[J].应用数学和力学, 2005, 26(8): 1003-1008.LI Jiang-teng, CAO Ping. Cusp catastrophe model of instability of pillar in asymmetric mining[J]. Applied Mathematics and Mechanic, 2005, 26(8): 1003-1008.

[8] 潘岳, 张勇, 吴敏应, 等. 非对称开采矿柱失稳的突变理论分析[J]. 岩石力学与工程学报, 2006, 25(Suppl.2): 3694-3702.PAN Yue, ZHANG Yong, WU Min-ying, et al. Analysis of catastrophe theory for pillar destabilization in dissymmetric mining[J]. Chinese Journal of Rock Mechanics and Engineering,2006, 25(Suppl.2): 3694-3702.

[9] 潘岳, 王志强, 张勇. 突变理论在岩体系统动力失稳的应用[M]. 北京: 科学出版社, 2008: 87-93.PAN YUE, WANG Zhi-qing, ZHANG Yong. Application of catastrophe theory for dynamic failure of rock[M]. Beijing:Science Press, 2008: 87-93.

[10] 秦四清, 王思敬. 煤柱-顶板协同作用的脆性失稳与非线性演化机制[J]. 工程地质学报, 2005, 13(4): 437-446.QIN Si-qing, WANG Si-jing. Brittle instability and non-linear evolution mechanism of the synergistic action of pillar roof system[J]. Journal of Engineering Geology, 2005, 13(4):437-446.

[11] Karcinovic D. Statistic aspects of the continuous damage theory[J]. Int.J Soils Structure, 1999, 18(7): 551-962.

[12] Thom R. Structural stability and morphs genesis [M]. New York:Benjamin Addison Wesley, 1997: 1-28.

[13] Zeeman E C. Catastrophe theory[J]. Scientific American, 1976,236(4): 65-83.

[14] 施泽进, 罗蛰潭, 彭大钧. 非线性地质勘探研究导论[M]. 成都: 四川科学技术出版社, 1995: 40-55.SHI Ze-jin, LUO Zhe-tang, PENG Da-jun. Introduction to nonlinear geological prospecting[M]. Chengdu: Sichuan Science and Technology Press, 1995: 40-55.

[15] 黄润秋, 许强. 工程地质广义系统科学分析原理及应用[M].北京: 地质出版社, 1997: 139-143.HUANG Run-qiu, XU Qiang. Theory and application of generalized systemic science analysis in engineering geology[M].Beijing: Geology Press, 1997: 139-143.

[16] 刘军, 秦四清, 张倬元. 缓倾角层状岩体失稳的尖点突变模型研究[J]. 岩土工程学报, 2001, 23(1): 42-44.LIU Jun, QIN Si-qing, ZHANG Zhuo-yuan. Study on cata strophic model with cusp point for failure of stratified rock mass with a gentle inclination[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 42-44.