Low-complexity transceiver design scheme based on channel null-space feedback
NI Ji-qing(倪吉庆), FEI Ze-song(费泽松), XING Cheng-wen(邢成文),KUANG Jing-ming(匡镜明)
(School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China)
Beamforming can improve the performance of multiple-input multiple-output(MIMO)systems.However,channel state information(CSI)is necessary for beamforming operation at the transmitter.Hence,how to obtain CSI is critical,especially for frequency-division duplex (FDD)systems where the downlink and uplink channels are not reciprocal.Accordingly,the application of limited feedback to multiple antenna wireless system has attracted lots of attention[1-2].
Most limited feedback multiuser MIMO schemes fall into two categories[3-5].One popular multi-user scheme is known as per user unitary rate control(PU2RC)[3-4].PU2RC systems use a deterministic codebook and precoding matrix should be unitary.They can be designed using probing or allowing the users to compute the signal-tointerference-and-noise ratio (SINR)for all code-word matrices.The other category is to let users quantize some function of the channel matrix,such as channel direction[5].However,inherent quantization error leads to a sum rate ceiling as the signal-to-noise ratio(SNR)increases.
To reduce the negative effect of quantization errors,a low-complexity transceiver design scheme for both the transmit beamformers and receive combining vectors based on channel null-space feedback is proposed in the two-user MIMO system.Compared to traditional precoding vector quantization or channel direction quantization,the users quantize local channel null-space in this paper.Then,the transmitter uses one user’s quantization vector as the other user’s transmit beamformer directly.Since the interference can be determined at the receiver,interference reject combining(IRC)could be jointly utilized to cancel the inter-user interference[6-7].The proposed transceiver joint design scheme can provide substantial sum rate benefits because the negative effect of channel quantization error is reduced.
1 System model
A two-user MIMO system is illustrated in Fig.1,where the base station(BS)sends data information to two users simultaneously.It is supposed that single data stream is transmitted for per user.The propagation channel is narrowband and flat-fading.Under the assumption of linear precoding,the transmitted signal intended for userk(k=1,2)could be given by:

wheresk∈CN(0,1)denotesthedatasymbolintendedforuserk,representsthepowerallocatedfordatasymbol,andwistheunitnorm beamformingvector(‖w‖=1)chosenfroma randomlygeneratedcodebook.BSissubjecttoa totalpowerconstraintofP.Bothtransmitterand receivermaintainacommoncodebookWwhich comprisesN:=2BbeamformingvectorsW:={v1,v2,…,vN},whereBisthenumberoffeedbackbits peruser.

Fig.1 System model with one BS and two users
Underaboveassumptions,thesignalreceived atuserkcanbedepictedas
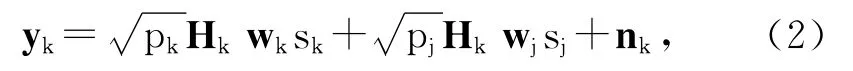
where{k,j}∈{1,2}andj≠k(throughout the following parts),Hkisthechannelbetweenthetransmitteranduserk,andnkisthewhiteGaussian noisewithmeanzeroandvarianceσ2.Thereceiver isassumedtoknowlocalperfectCSI.TheBSis onlysupposedtohavequantizedchannelinforma-tion.
Whenthereceivertreatstheco-usertransmissionsasnoiseandthepowerisallocatedequally betweenthetwousers,thereceivedSINRatuserkisdescribedas

whereMis the multiplexing gain and equal to 2in this paper.Since the beamforming vector wkisobtainedfromthequantizedcodebook,theinterferenceterminthedenominatorofEq.(3)isnotzero.Andtheinterferencetermdirectlydependson thequantizationerrors.
Westudythelong-termaveragethroughput,andcouldgettherateattheuserkas
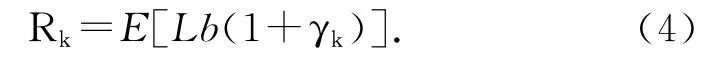
By symmetry,the system sum rate can be given by

2 Transceiver design scheme
2.1 Null-space feedback scheme
In this subsection,the feedback scheme based on channel null-space quantization is described in detail.In traditional feedback schemes,receiver usually quantizes the channel vector(or channel matrix)directly.Herein,the null-space of channel matrix is quantized and feedbacked.Both transmitter and receiver maintain a common codebook WthatcomprisesNvectors.Eachreceiverisassumedtouseadifferentandindependentlygeneratedquantizationcodebook.Ifacommoncodebookisused,therewouldbeanon-zeroprobability thatmultipleusersreturnthesamequantization vector,whichreducesthenumberofspatialdimensionsavailable[8].Firstofall,theuserchoosescodewordthatisclosesttothechannelnullspaceinthecodebookasquantizationvector:

where ckisthequantizedvectorforuserk,null(Hk)isthenull-spaceofHkand〈· ,·〉de-notestheinnerproductoperationoftwovectors.Thentheusersendstheindexofselectedcodeword backtothetransmitter.Thetransmitterusesone user’squantizationvectorastheotheruser’spercodingvectordirectly:

wherewiisthenormalizedbeamformingvector,i=1,2.(‖w‖=1).Whenthequantizationvector isinthenull-spaceofchannel,multi-userinterferencecanbeeliminatedcompletely.Basedonthe limitedfeedbacksetting,theinterferenceterm cannotbezerobecausethechannelquantizationerrorsexist.Andwhenthenumberoffeedbackbitis fixed,thesystembecomesinterferencelimited.
2.2 Interference rejection combination
Inthisproposednull-spacefeedbacksystem,theusersendsthetransmitbeamformeroftheinterferenceuserbacktotheBS.Sincetheinterferenceinformationcanbeknownatthereceiver,IRCcanbejointlyutilizedtocanceltheinter-user interference.Inthissubsection,wewilldiscuss theproposedreceivingcombinationschemeatthe receiver.Becausethenegativeeffectofchannel quantizationerrorisremoved,thismethodimprovesthesumrateperformancegreatlyandthe sumrateceilingvanishes.Forsimplicity,the powerofthetransmitterisassumedtobe1andallocatedequallybetweentheusers.Thenthesignal receivedatuserkcanbedepictedas
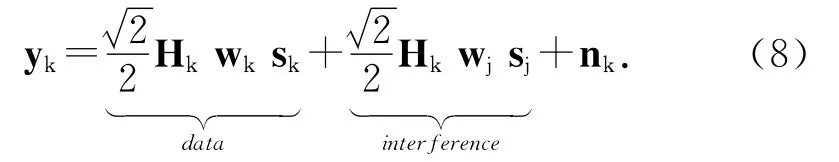
The above equation can also be expressed as follows equivalently:

where hekdenotestheeffectivechannelvectorbetweenthetransmitteranduserkandhek=/2 Hkwk,fkdenotestheeffectiveinterference channelfk=/2 Hkwj,andukisdenotedasthe sumoftheinterferenceandnoise.Here,weusegktorepresentthenormalizedcombiningvector(‖gk‖=1).TheresultingSINRatthereceiver isgivenby

whereRuuisthecovariancematrixofinterference andnoise.Itisknownthatnoiseisassumedtobe whiteandisindependentoftheinter-userinterference.Therefore,thecovariancematrixcanbe formulatedas

wherefisknownatthereceiverbasedontheproposedfeedbackscheme.WhentheSINRisobtainedbyEq.(10),thesystemsum-rateisgiven byEq.(5).Inordertomaximizethesum-rate,anoptimizationproblemcanbeformulatedas

According to the theory of generalized Rayleigh quotient[6],the optimal combining vector is given by

The receiving combining vector could whiten the interference to reduce the negative effect of quantization errors.
Compared to traditional maximum-ratio combining(MRC)technique,IRC considers the interuser interference.Based on the proposed null-space feedback scheme,the receiver can compute the covariance matrix of interference and noise with low complexity.Hence,the proposed transceiver design scheme based on channel null-space quantization can improve the sum rate greatly and reduce the negative effect of channel quantization errors.
3 Simulation results
In this section,numerical results of the proposed joint design scheme for both the transmit beamformers and receive combining vectors are presented and are compared with the traditional method using channel direction quantization.It’s assumed that the BS is equipped with four antennas and each user is equipped with two antennas.All the simulations are based on flat fading Rayleigh channel and random vector quantization (RVQ).And the power is allocated equally between the two users.Figs.2-3show that simulation performance comparison between traditional zero-forcing beamforming(ZFBF)with maximum ratio combining(MRC)and the proposed transceiver design scheme.

Fig.2 BER performance comparison between ZFBF with MRC and the proposed design scheme
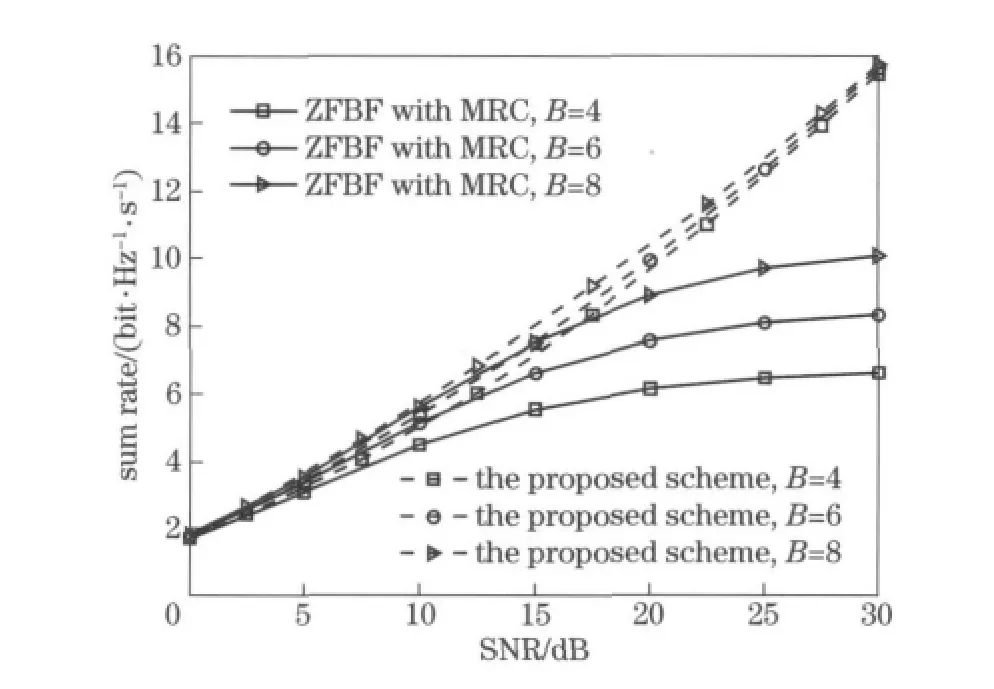
Fig.3 Sum-rate performance comparison between ZFBF with MRC and the proposed design scheme
In Fig.2,the BER performance comparison between traditional feedback scheme with MRC receiver and the proposed joint design scheme is presented.From Fig.2,it can be seen that simulation results support above theory analysis.As expected,the proposed joint design scheme outperforms the traditional method significantly especial-ly at high SNR.This is the reason that the IRC receiver can whiten the interference and the negative effect of quantization errors is compressed.And the bigger the number of feedback bit,the better the performance of the system.When the number of feedback bit is fixed,the system becomes interference limited.
In Fig.3,we give sum rate performance based on joint design scheme and compare it with traditional MRC receiver.It can be easily seen that proposed joint design scheme based on channel nullspace quantization improves the system performance greatly.In traditional feedback system,number of feedback bit dominates the system performance.The system performance approaches a sum rate ceiling as the SNR increases when the number of feedback bit is fixed.Even if the number of feedback bit is large,the system performance is also limited because of the channel quantization errors.While the proposed joint design scheme can obtain satisfied performance even with small feedback bits.In practical system,the number of feedback bit is usually fixed and cannot be too large.Hence,the proposed joint design scheme can improve the system performance effectively without increasing the number of feedback bit.
4 Conclusion
In this paper,a low-complexity transceiver joint design scheme for both the transmit beamformers and receive combining vectors is proposed in the two-user MIMO system.The user quantizes the null-space of channel and sends it back to the transmitter.And then,the transmitter uses one user’s feedback vector as the other user’s precoding vector directly,i.e.,one user’s feedback vector based on channel null-space quantization is used as the other user’s transmit beamformer directly.Therefore,the user knows of PMI working on the interference user and is able to cancel the interference effectively by utilizing IRC at receiver.Even if the number of feedback bit is fixed and small,sum-rate improvement can also be achieved especially at high SNR.The joint design scheme based on channel null-space feedback could be extended to multiple-cell coordinated scenarios.
[1]Love D J,Heath R W,Lau V K N,et al.An overview of limited feedback in wireless communication systems[J].IEEE Journal on Selected Areas in Communications,2008,26(8):1341-1365.
[2]Love D J,Heath R W,Santipach W,et al.What is the value of limited feedback for MIMO channels?[J].IEEE Communication Magazine,2004,42(10):54-59.
[3]Kim H,Lee K B.Limited feedback signaling for MIMO broadcast channels[J].IEEE Workshop on Signal Processing,2005,22:855-859.
[4]Kim C S,Kim H,Lee K B.Adaptive precoding for wireless MIMO broadcast channels with limited feedback[J].IEICE Transactions,2005,88-B(11):4237-4245.
[5]Jindal N.MIMO broadcast channels with finite-rate feedback[J].IEEE Transactions on Information Theory,2006,52(11):5045-5060.
[6]Winters J.Optimum combining in digital mobile radio with cochannel interference[J].IEEE Transactions on Vehicular Technology,1984,33(3):144-155.
[7]Erik G L.Model-averaged interference rejection combining [J].IEEE Transactions on Communications,2007,55(2):271-274.
[8]Santipach W,Honig M L.Signature optimization for CDMA with limited feedback[J].IEEE Transactions on Information Theory,2005,51(10):3475-3492.
(Edited byCai Jianying)
 Journal of Beijing Institute of Technology2012年2期
Journal of Beijing Institute of Technology2012年2期
- Journal of Beijing Institute of Technology的其它文章
- Effects of laser beam divergence angle on airborne LIDAR positioning errors
- Large deflection of annular throttle-slices in shock absorbers
- Active contours with normally generalized gradient vector flow external force
- Bicycle capacity of borrowed-priority merge at unsignalized intersections in China
- Distribution of driving trajectory of passenger car in highway horizontal curves
- Development of an occupant restraint system model and parametric study on equivalent crash pulse in vehicle frontal offset crash
