浅析内燃机缸内三种湍流涡黏度模型

邹振宇 刘 晶 李 义

(1:吉林建筑工程学院土木工程学院，长春 130118;2:国家开发银行吉林省分行，长春 130021;3:长春医学高等专科学校，长春 130031)

1 研究内燃机缸内三种湍流涡黏度模型的意义

内燃机作为最常见的燃烧装置之一，广泛应用于工农业生产和交通运输等各个领域.据统计，内燃机所消耗的能源占世界石油消耗总量的60%.由于世界范围内化石能源的日益短缺和环境污染的日益加剧，人们对内燃机燃烧与排放性能的研究给予了越来越多的关注.

内燃机缸内流场结构和湍流特性是控制燃烧过程的最重要因素之一，在内燃机整个工作循环中，其缸内流体始终进行着极其复杂而又强烈瞬变的湍流运动.实验和理论计算都表明，缸内湍流流动的主要来源是进气射流通过气阀时产生的强烈剪切层以及射流与缸壁的碰撞.缸内湍流流动是一个包括湍流剪切、压缩或膨胀、回流和边界层的复杂结构，它是不稳定的三维流动.这种湍流流动是内燃机工作和燃烧过程中各个物理化学子过程的一个共同的基础.它决定了各种量在缸内的输运及其空间分布，它对可燃混合气的形成及其浓度场、火焰传播速度和燃烧品质、缸内的传热及污染物的形成等等具有直接的本质的影响.因此，要正确地模拟和分析内燃机的燃烧和排放，就离不开对缸内湍流的正确描述和模拟.

几十年来，人们通过多种类型的实验方法对缸内湍流进行测量和分析.例如，用激光多普勒技术研究缸内流体的速度场和湍流特性［1－4］，研究喷雾粒子的速度分布情况［5］;利用远红外光谱分析法测量缸内气体的温度［6］等等.这些工作为人们认识内燃机缸内湍流流动过程的机理，改善内燃机性能，降低排放污染指标，起到重要的作用.

缸内湍流具有“三强一异”特点，即强不定常性，强压缩性，强旋转性和各向异性.这些特点使得它与其他各类燃烧系统中的湍流相比最具复杂性和典型性.只靠实验来获得缸内流场数据，不仅耗资大、周期长，而且完全相似的实验模拟几乎是不能实现的.随着计算机技术的飞速发展，对缸内过程的数值模拟占据了越来越重要的地位.湍流的数值模拟以实验和流体力学的基本理论为基础，通过计算流体力学的方法来预测内燃机工作循环中缸内流体运动的发展和变化.它具有周期短、费用低、信息量大、实用性强、能反映几何形状及各工况参数的影响等特点.

迄今为止，由于人们对湍流机理尚缺乏透彻了解，以致现有的湍流模型都还不完善.因此，用各种模型计算得到的结果与实际还有一定差距，这当然与数值算法的精度等有一定的关系，但主要还是由于数学模型不能完全正确地反映流动的物理机理而造成的.因此，发展能精确描述湍流特性的数学模型既是解决工程实际问题，又是我们从理论上去探索缸内湍流流动特点与规律的最有效现实手段.

因此，对于内燃机缸内湍流流动的研究意义重大.目前，湍流模型的数值模拟已经成为内燃机领域中的热点，许多研究者致力于对模型的改进和研究上，并已取得显著的进展.

2 内燃机缸内三种湍流涡黏度模型原理

2.1 标准k－ε模型

在湍动能k方程的基础上，再引入一个关于湍动耗散率ε的方程，即形成了k－ε模型［7］.在模型中，表示湍动耗散率(turbulent dissipation rate)的ε被定义为:

这里，上标“－”代表对时间的平均值，“'”代表脉动值.物理量的瞬时值为时均值与脉动值之和:ui=+ui′.湍动黏度μt可以表示成k和ε的函数，即:

在标准的k－ε模型中，k和ε是两个基本的未知量，与之相对应的输运方程:

其中，Gk是由于平均速度梯度引起的动能k的产生项.由下式计算:

Gb是由于浮力引起的湍动能k的产生项;对于不可压流体，Gb=0.对于可压流体，有:

其中，Prt为湍动Prandtl数，在该模型中，Prt=0.85;gi为重力加速度在第i方向的分量;β为热膨胀系数，可由可压流体的状态方程求出，其定义为:

YM代表可压湍流中脉动扩张的贡献，对于不可压流体，YM=0;对于可压流体，有:

其中，Mt为湍动Mach数，Mt=;a为声速，a=;σk和σε分别为与湍动能k和耗散率ε对应的Prandtl数;σk=1.0，σε=1.3;Sk和Sε为用户定义的源项.在标准的k－ε模型中，根据Launder等的推荐值及后来的实验验证，模型常数C1ε=1.44，C2ε=1.92，Cμ=0.09，对于不可压流体的流动计算中与浮力相关的系数C3ε，当主流方向与重力方向平行时，有C3ε=1.0，当主流方向与重力方向垂直时，C3ε=0.

根据以上分析，当流动不可压时，且不考虑用户自定义的源项时，Gb=0，YM=0，Sk=0，Sε=0，这时，标准的k－ε模型方程为:

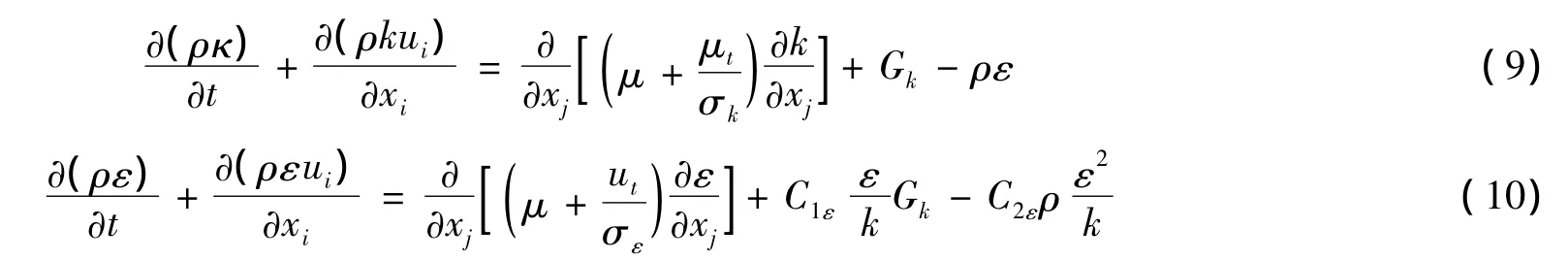
方程(9)和(10)中的，按其展开式(11)计算:

2.2 RNG k－ε模型

利用重整化群(Renormalization Group，RNG)理论提出了RNG k－ε模型［8］.它的基本思路是通过在空间尺度上的一系列连续的变换，对原本十分复杂的系统或过程实现粗分辨率或“粗粒化”(coarse grained)的描述，从而使问题得到简化而易于处理.

2.3 realizable k－ε模型

在RNG k－ε模型的基础上，认为湍动黏度计算式中的系数Cμ不是常数，应与应变率联系起来.从而提出了realizable k－ε模型，这里realizable有“可实现”的意思.

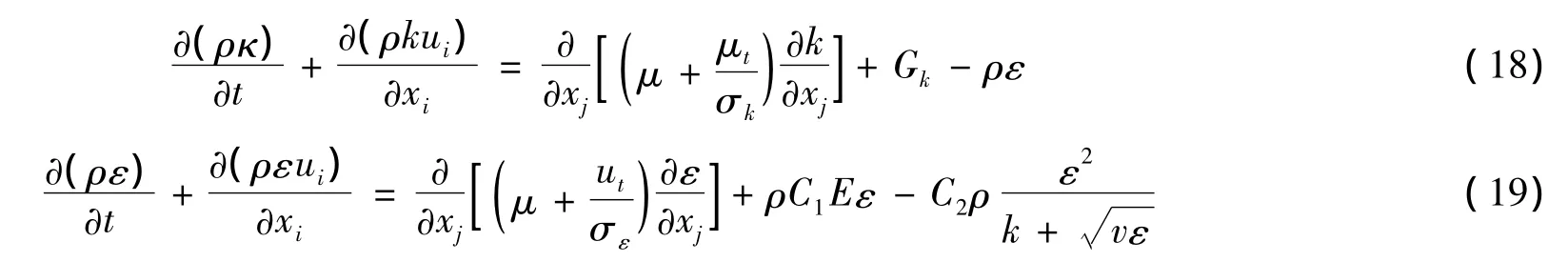
其中，σk=1.0，σε=1.2，C2=1.9

式(18)中，Cμ和μt按下式计算:

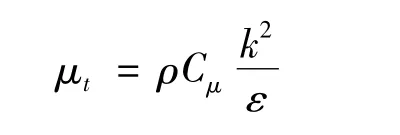
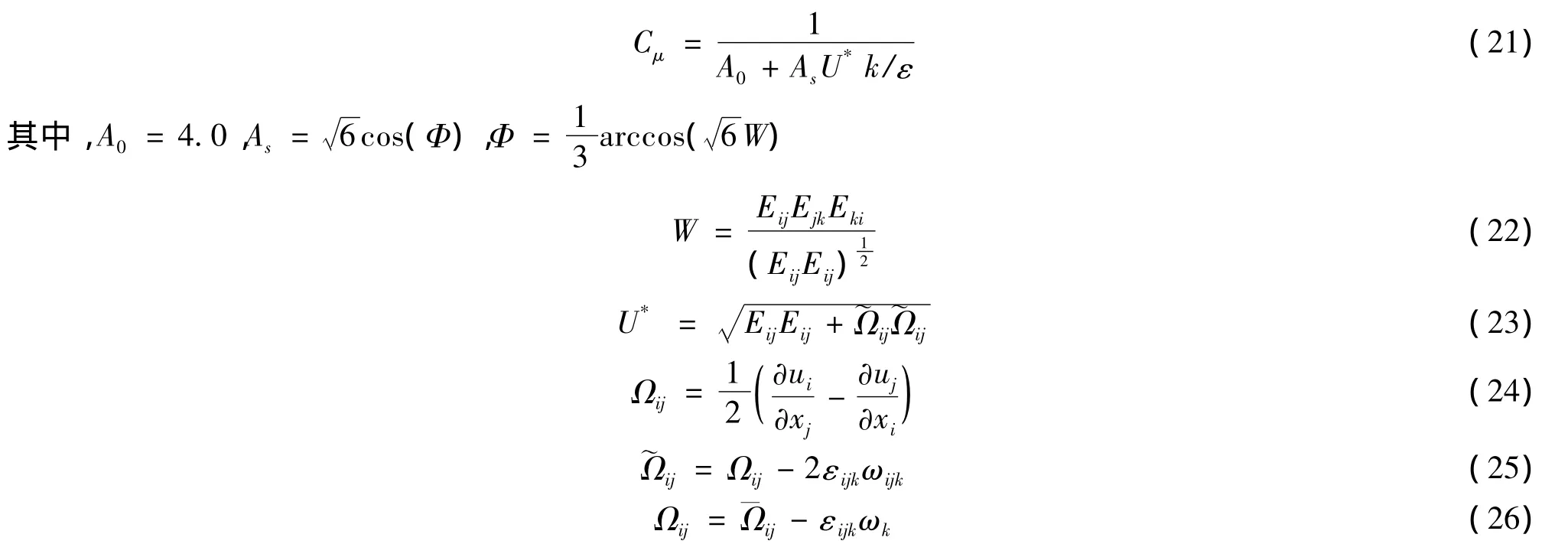
3 内燃机缸内三种湍流涡黏度模型特点对比

3.1 标准k－ε模型的特点

标准k－ε模型逐渐发展成最成熟，应用最广泛的模型，且成功地用来计算各种不同类型的湍流运动.标准k－ε模型比零方程模型和一方程模型有了很大改进，在科学研究及工程实际中得到了检验和成功应用.但用于强旋流、弯曲壁面流动或弯曲流线流动时，会产生一定的失真.原因是在标准k－ε模型中，对于Reynolds应力的各个分量，假定黏度系数μt是相同的，即假定μt是各向同性的标量.而在弯曲流线的情况下，湍流是各向异性的，μt应该是各向异性的张量.

3.2 RNG k－ε模型的特点

与标准的k－ε model比较，RNG k－ε模型的主要变化是:

(1)通过修正湍动黏度，考虑了平均流动中的旋转及旋流流动的情况;

(2)ε方程中增添了一项，从而反映了主流的时均应变率Eij，这样，RNG k－ε模型中生成项不仅与流动情况有关，而且在同一问题中也还是空间坐标的函数.

RNG方法对描述对象有一个基本要求，就是系统必须具有尺度不变性，即对系统而言，不存在一个由外部环境所施加的特征长度和时间尺度.换言之，系统应具有自相似性.RNG理论与分形理论也有不少相似之处.它们都是建立在研究对象具有自相似结构的基础上，且都是通过不断改变观测尺度来研究过程中包含的不变因素.只不过分形是以几何体作为研究对象，而RNG是以物理量为研究对象.但是此模型毕竟只是一个涡黏度模型，和其他类似的模型一样，它也使用了各向同性，局部平衡，单一特征长度等假设，对复杂的流动有一定的局限性［9］.

3.3 realizable k－ε模型的特点

与标准的k－ε模型比较发现，realizable k－ε模型主要变化是:

(1)湍动黏度计算公式发生了变化，引入了与旋转和曲率有关的内容;

(2)ε方程发生了很大变化，方程中的产生项不包括含有k方程中的产生项Gk，这样，现在的形式更好地表示了湍流能谱，即不同尺度涡团之间的能量转换;

(3)ε方程中的倒数第一项不具有任何奇异性，即使k值很小或为零，分母也不会为零.这与标准k－ε模型和RNG k－ε模型有很大区别.

4 内燃机缸内三种湍流涡黏度模型适用范围

通过以上对内燃机缸内三种湍流涡黏度模型原理的分析及特点的总结，我们得出三种模型的适用范围如表1.

表1 内燃机缸内三种湍流涡黏度模型适用范围

5 结论

笔者对内燃机缸内三种湍流涡黏度模型即标准k－ε模型，RNG k－ε模型和realizable k－ε模型做了详细的分析与总结，在分析了三种模型原理的上，总结出了各个模型的自身特点和适用范围.本文的工作对内燃机缸内流体流动模型理论做了很好的分析与总结，其结论对正在专研内燃机缸内流体研究的科研工作者有很强的借鉴意义.

［1］Faster R.An LDV System for Turbulence Length Scale Measurements，ASME 105 the Winter Annual Meeting［J］.Dec1984.

［2］Matsuoka S，et al.LDA Measurement and a Theoretical Analysis of the In － Cylinder Air Motion in a Diesel Engine，SAE paper［J］.850106.

［3］Ahmadi－ Befrui B，et al.Calculations and Measurements of the Flow in a Motored Model Engine and Implications for Open － Chamber Direct Engines［J］.In Three Dimensional Turbulent Shear Flows(Eds.S.Carmi，et al)1982，1 －9(American Society of Mechanical Engineers).

［4］Arcoumains C，Bicne AF.，Whitelaw JH.Squish and Swirl－ Squish Interaction in Motored Engines Fluids Engineering［J］.1983，105:105 －112.

［5］Wu KJ，Coghe A，Santavicca DA.，Bracco FV.LDV Measurement of Drop Velocity in Diesel－ type Sprays，AIAA［J］.1984，Vo122:1263 －1270.

［6］Myers P S，Uyehara O A.Accuracy and representation results obtained with an infrared pyrometer measuring compression temperature［J］.Proc.Inst.Mech.Engrs，180，Part 3G，83，1965.

［7］B.E.Launder，D.B.Spalding.Lectures in Mathematical Models of Turbulence.Academic Press［J］.London，1972.

［8］V.Yakhot，S.A.Orszag SA.Renormalization Group analysis of turbulence，A basic theory.J of Scientific Computing［J］.1998，1(1):1 －51.

［9］姜宗林，陈耀松.关于RNG代数湍流模型的研究.力学学报［J］.1995，27(1):99－103.