一种内置式永磁同步电动机的非线性转矩控制方法

傅华娟，周洪如，段 娜

(1.常州机电职业技术学院，江苏常州213164;2.中国重汽(香港)有限公司技术发展中心动力设计院，山东济南250000)

0 引 言

由于内置式永磁同步电动机的高能量密度和单位体积的大转矩，以及良好的弱磁能力，越来越受到人们的欢迎，尤其是在电动汽车用驱动电机上。内置式永磁同步电动机一个内在的特点就是凸极率很大，可以利用它产生磁阻转矩，而磁阻转矩与交直轴电流的乘积成正比。为了充分发挥凸极率大的潜能和确保单位电流产生的转矩最大，即使在恒转矩区，直轴电流也不能为零。直轴电流命令不为零，因此，系统就呈现出非线性，要想严格地解耦出励磁电流和转矩电流就很困难。现在的问题就是如何保证单位电流产生的转矩最大的条件下根据电机转子的速度、直流母线电压和转矩命令来决定直轴和交轴的电流命令的大小。由于汽车用电机要求很宽的恒功率范围，必须要注意电机的电压和电流的极限值。在额定转速以下，电机的转矩仅仅由最大电流极限限制，额定转速以上，也要考虑电压极限［1］。

高性能驱动系统的重要特征是快速性和精确的速度响应、扰动下快速的回复能力和参数的不敏感性，以及在多个速度运行范围的鲁棒性。但是对于内置式永磁同步电动机来说，由于绕组电流的非线性耦合，要实现精确的速度控制就很困难。

对于转矩和id－iq电流命令的非线性关系，本文采用泰勒级数展开的方法，不需要查询表格，并且计算量也很小。最后在MATLAB/Simulink进行了验证，证明了本文算法的有效性。

1 内置式永磁同步电动机数学模型

在d/q转子旋转坐标系上，内置式永磁同步电动机的电压方程:

电机的转矩公式:

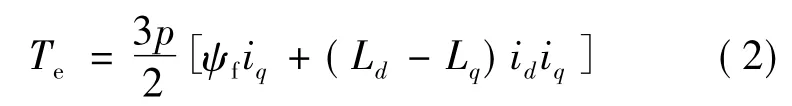
永磁同步电动机的电压和电流是由下面的条件限制的:

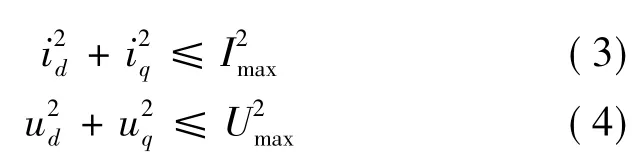
另外有:

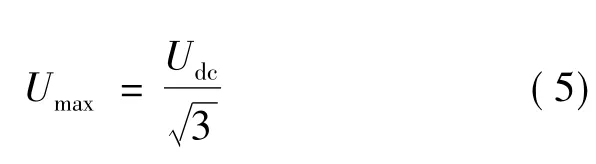
考虑到内置式永磁同步电动机在稳态和高速状态运行时，电阻的电流很小，于是忽略电阻的压降，由式(1)和式(4)直接推出以下公式:

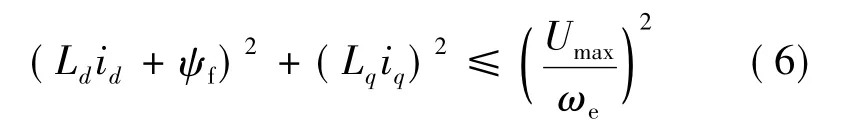
式中:ud、uq为 d、q 轴电压;id、iq为 d、q轴电流;R 为定子电阻;Ld、Lq为d、q轴电感;ωe为电机的电角速度;ψf为电机转子永磁体;Imax为空间矢量的定子电流最大值;Udc为直流母线电压;p为电机极对数。

2 内置式电机转矩非线性控制算法

2.1 驱动系统的工作原理

内置式永磁同步电动机驱动系统本质上包括电流控制器和速度控制器。速度控制器根据速度命令和反馈回来的实际速度产生转矩命令。接下来，根据转矩命令产生d轴和q轴的电流命令，再根据电流传感器反馈回来的实际电流，通过两个电流控制器产生电压控制命令，再由帕克反变换转换为静止两相坐标系下的电压，然后由空间矢量调制法调制出6个PWM脉冲信号来控制功率器件实现电机控制所需要的三相电压。如图1所示。

因此，电机矢量控制所需要的反馈量为转子位置信号、速度以及定子电流。

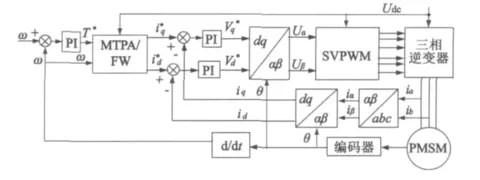
图1 内置式电机驱动控制系统总图

2.2 最大转矩/电流速度控制器

电机的速度控制器根据速度命令和反馈回来的实际速度来产生转矩命令。从式(2)直接可以看出，内置式永磁同步电动机的一个主要问题就是转矩与的非线性关系。在实际的内置式永磁同步电动机驱动系统中采用的最大转矩/电流(MTPA)控制策略可以使电机在单位电流下产生出最大转矩，由于最大转矩/电流控制策略使电机在额定转速以下的驱动效率最优化，因此成为了驱动系统首选的控制策略［5］。

式(7)为最大转矩/电流控制策略下的id、iq的关系式:

把式(1)代入到式(2)中，可以得到iq与Te的非线性关系式:

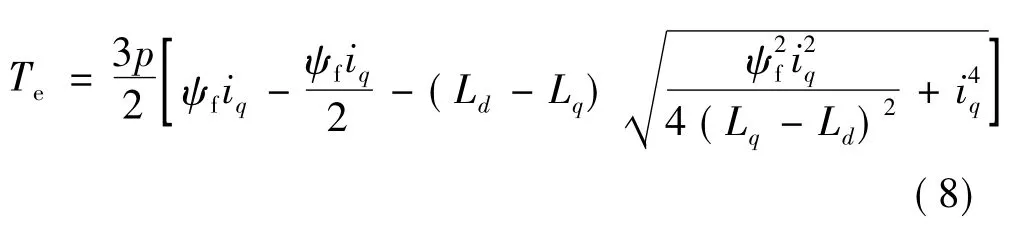
由于公式中包括根号开方运算，对于驱动系统实时执行来说，运用式(2)和式(3)就很困难。下面提出一种简化的转矩和d－q轴电流关系式，它通过利用泰勒级数展开的方法把式(3)的平方根项展开得到。

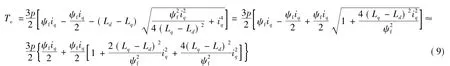
忽略高阶项，得到:

试验电机参数如表1所示。把表1中的试验电机参数代入可以得到:

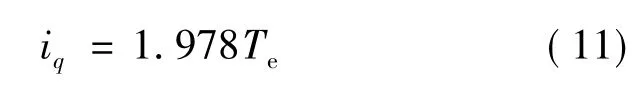
考虑到iq远大于零的时候，本方法有弊端，经过反复验证，给本方法的泰勒级数展开乘以一个补偿系数 0.935，得到:

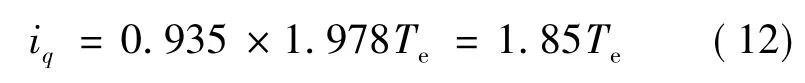
然后根据式(7)推导出id。

2.3 弱磁模式速度控制器

内置式永磁同步电动机具有相对大的电枢电感，可以实现较宽范围的弱磁控制，它是保证永磁同步电动机实现高速运行的重要控制模式，其核心是减小电机的气隙磁通，从而使电机在高速运行时端电压保持恒定。永磁同步电动机的励磁磁动势是由永磁体产生，无法调节。仅能通过调节定子电流，即增加定子直轴去磁电流去磁分量来保持高速运行时的电压平衡，从而达到弱磁扩速的目的［5］。下面是弱磁控制模式下id、iq的关系式:

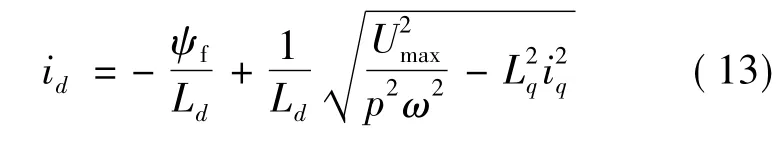
将式(5)代入式(2)中，可以得到iq和Te之间的非线性关系:

与式(4)类似，将式(6)在iq=0处泰勒展开，并且忽略高阶项，可以得到:

将表1中的试验电机参数代入到式(14)中并且对泰勒级数进行系数补偿，可以得到:

这时，可以从式(13)中推导出id。

3 仿真试验结果

为了证实所提出算法的有效性，在MATLAB/Simulink中的进行仿真验证。图2～图5仿真试验状态为:电机从静止起动到8 000 r/min的加速过程曲线，其中负载转矩为40 N·m，整个过程经历了从最大转矩/电流控制模式到弱磁控制模式，下面分别详细分析图2～图5的仿真结果。

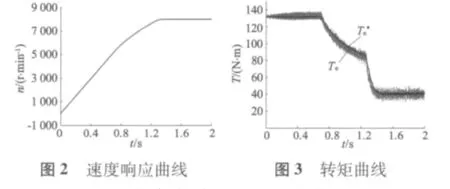
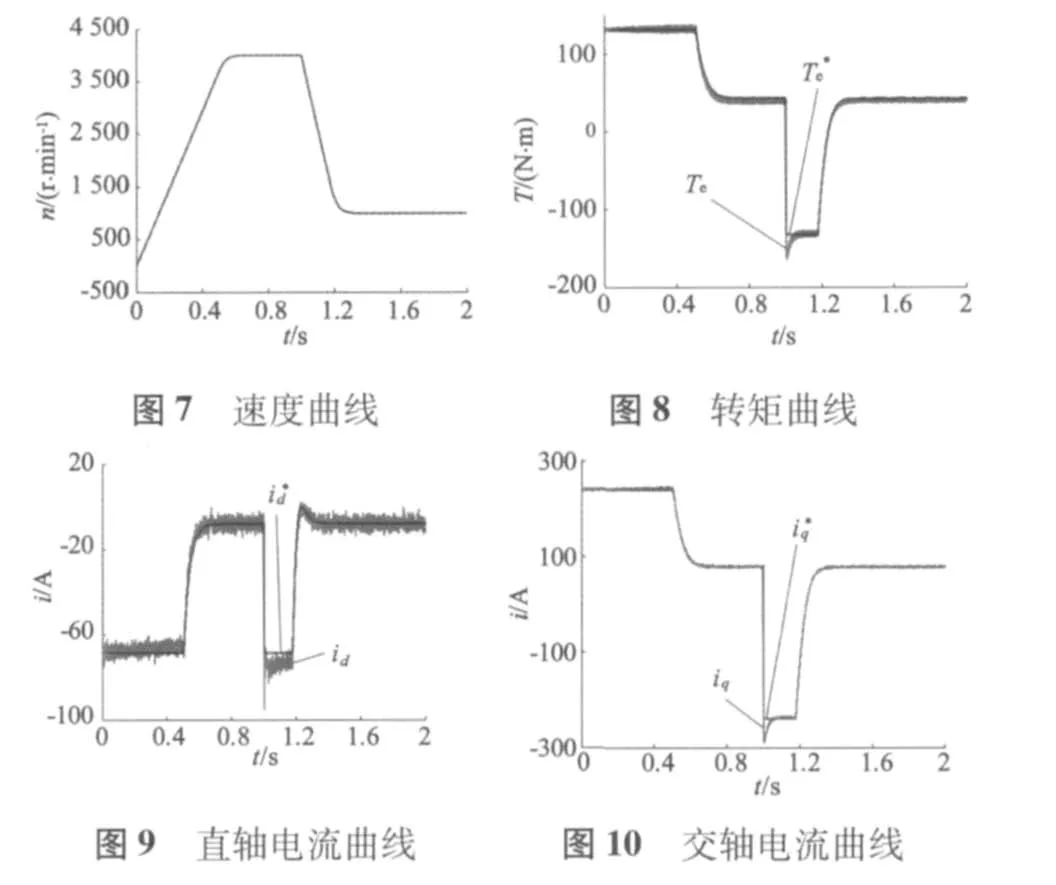
图2的速度曲线说明了电机在负载转矩为40 N·m，从零速度开始加速到8 000 r/min的整个过程的稳定性和响应的快速性。

图3是电机在负载转矩为40 N·m，从零速度开始加速到8 000 r/min的整个过程的转矩命令和实际输出的转矩值的曲线;图4是电机电流命令和实际检测的电流id对比曲线;图5为电机电流命令和实际检测的电流iq的对比曲线。

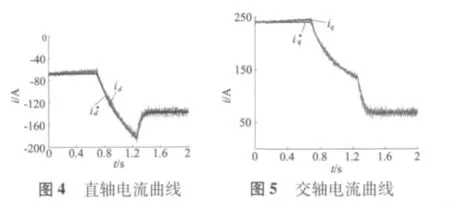
图6是从零速度开始加速到8 000 r/min的整个过程的电流命令曲线(O－A－B－C)。其中圆弧(实线)是最大电流圆;椭圆弧(虚线)是电压极限椭圆线(式(6))，不同的速度椭圆半径不同。图中曲线从O到A的过程，电机运行在最大转矩/电流模式，曲线A－B－C的过程，电机经历弱磁控制进入稳定速度的控制模式。

图7～图10是电机负载转矩为40 N·m从静止起动到4 000 r/min，1 s后速度降至1 000 r/min的整个过程速度仿真曲线。

图6 加速过程电流命令曲线(O－A－B－C)

4 结 论

本文对内置式永磁同步电动机中的电流命令与转矩命令间的非线性关系，采用泰勒级数展开的方法实现了转矩命令和交、直轴电流命令的关系的线性化。所提出的方法具有以下优点:

(1)不需要查表;

(2)能够充分利用电源电压;

(3)计算量小;

(4)包括最大转矩/电流(MTPA)和弱磁(FW)两种模式。

仿真结果充分证明了以上所提出的这些特征和方法的可行性。

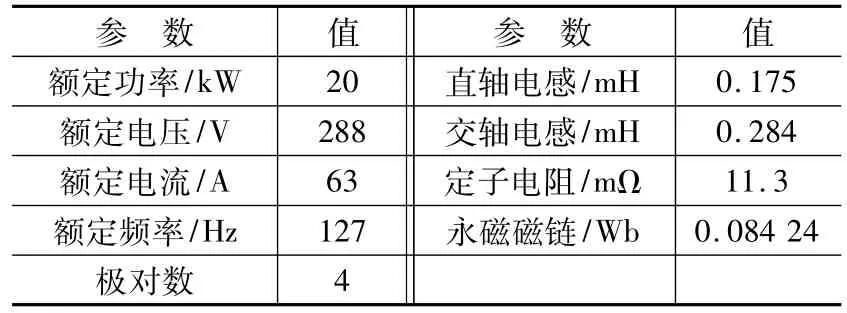
表1 电机参数

［1］王成元，夏加宽.电机现代控制技术［M］.北京:机械工业出版社，2006.

［2］吴卫安.永磁同步电机调速系统研究［D］.武汉:华中科技大学，2007.

［3］Choi G Y，Kwak M S，Kwon T S，et al.Novel flux － weakening control of an IPMSM for quasi six－step operation［C］//IEEE IAS Annual Meeting.2007:1315 －1321.

［4］Lenke R U，Doncker R W D，Kwak M S，et al.Field weakening control of interior permanent magnet machine using improved current interpolation technique［C］//IEEE PESC，2006:1 －5.

［5］Lin Ping － yi，Lai Yen － shin.Novel voltage trajectory for flux weakening operation of surface mounted PMSM Drives［C］//IEEE IAS Annual Meeting.2008:1－8.