地下水位变化对盾构隧道的影响研究

李春良，王 勇，张 巍

(1.吉林建筑工程学院交通科学与工程学院，长春 130118;2.吉林省公路管理局，长春 130021;3.吉林大学第二医院基建处，长春 130021)

0 引言

盾构隧道结构通常埋置在地表10 m以下，绝大多数的隧道都处于地下水位线以下，并长年受到地下水升降的影响。另外，由于近几年人类大量的取水活动以及目前的南水北调工程的影响，常导致相关地区地下水位线发生变化。此时，如果盾构隧道埋置其中，必然会受到地下水位变化所产生的影响，盾构隧道的内力和变形也会随着地下水位的升降而变化。大量工程实例也证实，地下水位的改变，会导致盾构隧道结构发生局部开裂、上浮及不均匀变形等力学状态的改变。

有学者对管片施工中的上浮问题进行了模拟，分析了盾构管片结构设置和衬砌背后注浆造成管片结构和周围地层的位移变化特点，并讨论了盾构隧道上浮的变化规律［1］，研究了盾构隧道在施工过程中，盾构机刚脱离盾尾的管片经常会出现局部或整体上浮的问题，并指出了水、浆液、泥浆等产生浮力的原因［2－3］。也有人对不同潜水水位和承压水头作用下盾构隧道的地表沉降、衬砌内力等进行了分析研究［4］。

可以看到，目前人们对盾构隧道的研究热点主要集中在对隧道建设过程中所引起的土体移动和变形问题方面［5－10］，而关于地下水位升降对盾构隧道结构的影响研究得并不多。因此，为使盾构隧道在施工、营运过程中避免地下水位变化而产生破坏，正确地认识地下水位变化对盾构隧道在受力与变形方面的影响势在必行。

本文针对地下水位的变化情况，采用有限元模拟方法对这一过程进行了分析，详细研究了地下水位上升后对盾构隧道结构在位移、变形等方面的影响状况，揭示出地下水位上升对盾构隧道结构的影响规律。

1 饱和土中盾构隧道的水压力模型

盾构隧道处于地下水位线以下时，地下水会对盾构隧道产生静水压强，由于静水压强具有垂直指向性和各向等值性，则作用在盾构隧道外围的静水压强分布如图1所示。

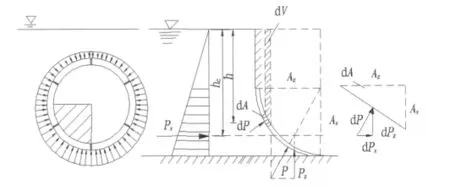
图1 隧道横截面上压强分布Fig.1 Pressure distribution on cross-section of shield-bored tunnel

根据作用在曲面上的压强分布可以发现，作用在此曲面上的各点压强方向不同，为非平行力系。为研究盾构隧道横截面任意点的水压力情况，将截面中各点的地下水压力分解为水平分力和铅垂分力，并分别求其代数和，而后便可求出作用在整个曲面上的静水总压力。

为方便研究，取图1中的阴影部分为研究对象，设h为dAx投影面积形心在自由表面以下的深度，则

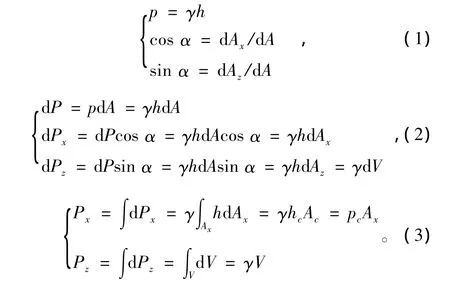
则隧道边壁受到的地下水总压力计算公式为

式中:α为总压力与水平线的夹角;pc为投影面积Ax形心处压强;γ为液体重度;V为研究对象的体积。

2 地下水位线变化的模拟过程

当盾构隧道所处地层中的地下水位发生变化时，受地下水影响的土层的参数和在其中管片的受力均发生变化。为反映出整个过程中各类土层参数和水压力变化等因素对隧道和土层产生的影响程度，用有限元理论模拟地下水位变化对盾构隧道的影响情况，分析不同水位变化后的盾构隧道结构在位移、变形等方面的变化规律。

根据所关注的问题和计算精度，建立一定范围的土体，并划分出盾构隧道结构、注浆层和管片结构，并对结构体进行网格划分。采用不同的网格划分技术在结构的关键部分指定节点位置，划分后的结构通过节点组成连续的单元。图2为地下水位线在盾构隧道周围土层中发生变化时的离散模型。

图2 地下水位线变化的模拟过程Fig.2 Simulation process of water level fluctuation

在有限元模拟过程中:1)先对盾构隧道的初始状态模拟计算，计算地表荷载、水压力、结构自重等，此时的计算结果作为管片受力的初始状态;2)当地下水位线发生改变时，承接初始状态的计算结果，对将受到地下水影响的土层的相关参数进行二次调整，并将地下水位变化后的压强差作用到隧道表面，揭示出地下水位变化后对盾构隧道及其周围土体的影响情况。

3 有限元模型的建立

3.1 模型的建立

在分析过程中，采用实体单元Solid45模拟管片、土层及注浆层结构，并利用网格单元Mesh200辅助完成整个结构的网格划分。

3.1.1 模型尺寸

取范围足够大的土体，避免小边界效应所产生的误差。计算中取的土体范围为:水平方向取80.2 m，向下取47.7 m，隧道掘进方向取60 m;隧道中心距离地表以下18.1 m，隧道管片外径为6.2 m，内径为5.5 m，管片厚度为0.35 m，隧道外围的注浆层厚度为0.25 m。有限元模型如图3—5所示。

3.1.2 边界约束

对模型体下底面上的所有节点的竖向位移进行约束，对模型体左右2个侧面上的所有节点的左右方向位移进行约束，对模型体前后2个面上的所有节点的前后方向位移进行约束。

3.2 模拟水位变化过程

为分析地下水位变化对隧道结构的影响，模拟计算了如下几个地下水位变化后的连续过程。

1)地下水位距隧道拱底下一定深度处(水位线距地面23.5 m)上升到盾构隧道拱底标高处过程。

2)地下水位由盾构隧道拱底标高处上升到盾构隧道中心标高处过程。

3)地下水位由盾构隧道中心标高处上升到盾构隧道拱顶标高处过程。

4 计算结果分析与讨论

4.1 竖向水压力差计算结果对比

为了验证有限元计算模型的准确性，利用公式(4)计算了不同高度情况下隧道受到的竖向水压力差，并与有限元模型计算得到的竖向水压力差进行了对比，如图6所示。由图6可以发现，根据有限元模型计算的竖向水压力值与理论公式计算的竖向水压力值较一致，表明有限元模型具有一定的精度与准确性，可以用来分析地下水升降对盾构隧道产生的水压力差问题。在图6中，当地下水位从0点标高(拱底标高)上升到拱顶标高时，隧道竖向水压力差逐渐增大，但并非为线性增加趋势。

图6 隧道竖向水压力差对比Fig.6 Relationship between vertical water pressures and water levels

4.2 隧道拱顶、拱底及其正上方地表的竖向位移随地下水位变化的结果

图7为隧道拱顶、拱底及其正上方地表的上升位移随地下水位变化曲线。

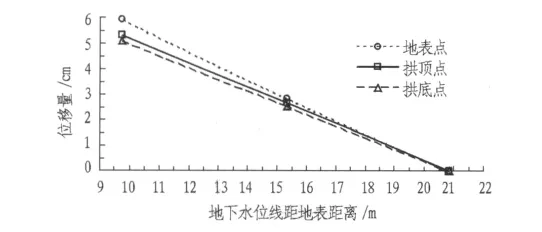
图7 拱顶、拱底及其正上方地表上升位移随地下水位变化曲线Fig.7 Upward displacement at crown，invert and above ground surface

由图7可以发现:

1)随着地下水位线的升高，隧道拱顶处位移、隧道拱底处上升位移及对应地表点的上升位移均变大。主要因为地下水升高后产生了向上的浮力，土中的孔隙水压力增加，土体间的有效应力减小，从而引起土层上升。由图7可以发现，随着水位线的升高，隧道产生的上升位移越来越大，并且拱顶处的上升位移大于拱底处的上升位移。

2)当地下水水位从隧道拱底标高处上升到隧道中心标高处时，地下水逐渐开始对隧道产生向上的浮力，但浮力仅作用于隧道中心线以下部分，此时隧道的上升表现为整体上升，且上升的位移量逐渐增大，但隧道的环向变形不明显。

3)当地下水水位从隧道中心线标高处上升到拱顶标高处位置时，隧道的四周均受到了水压力作用，隧道结构开始产生径向变形，同时隧道拱顶、拱底和地表继续上升;但拱顶处的上升位移大于拱底处的上升位移，主要由于隧道拱顶处受到的约束相对于拱底位置的约束要弱，因为上覆土层的厚度小于拱底上覆土层的厚度。

4.3 地下水位变化后隧道边壁的侧向位移

为研究地下水位变化过程中隧道边壁的侧向位移情况，绘制了盾构隧道中心标高位置上侧向边壁的侧向位移曲线，如图8所示。由图8可知，随着地下水位的升高，隧道中心标高处的边壁也发生了一定量的向内的水平侧向变形。主要是由于地下水对隧道产生的径向水压力引起的，并且地下水位越高，隧道边壁的水平侧向变形越大。

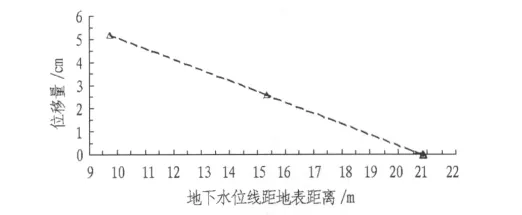
图8 隧道中心线标高处边壁的侧向位移Fig.8 Lateral displacement of side wall at tunnel center line elevation

4.4 隧道纵向30 m处横断面内各地表点竖向位移变化

根据有限元模拟计算结果，绘制出地下水位线由初始位置(水位线距地面23.5 m)上升到拱底标高、隧道中线标高及拱顶处标高位置后，在隧道纵向30 m处横断面内的地面点的竖向位移曲线，如图9所示。

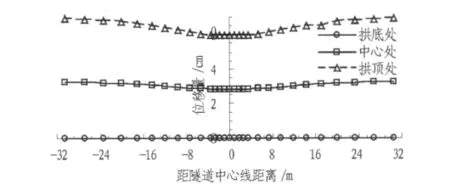
图9 隧道纵向30 m处横断面内各地表点竖向位移Fig.9 Vertical displacements

由图9可以发现:

1)地下水位线由初始位置上升2.65 m后，地表各点的竖向上升位移几乎为零，表明地下水位线小幅度上升对地面几乎不会产生影响。

2)当地下水位线由初始位置上升到隧道中心线标高处位置时，地表各点均上升，但横向各点上升的位移量不同，盾构隧道上方的地表点上升的位移量小于其下方没有隧道的地表位移量。主要因为地下水位上升，土的自重应力降低，土体发生向上的位移，同时隧道中心线标高以下的拱底区域受到水的浮力也发生上浮，但隧道的上浮量小于土层的上浮量，所以隧道结构在一定程度上阻碍其下方土体的上浮。因此，盾构隧道上方的地表点上升的位移量小于其下方没有隧道的地表位移量。

3)当地下水位线由隧道的中心线标高处上升到隧道的拱顶标高处时，地表土体的上升量达到了5.8 cm。

5 结论与讨论

1)本文建立了地下水位变化时盾构隧道结构的有限元模型，该模型可预测出地下水位上升时对盾构隧道产生的影响，揭示出地下水位上升所导致土层内部应力状态和沉降位移的改变情况。

2)地下水位的上升会使地表土体发生回弹，但盾构隧道上方土体的回弹值要小于其下方没埋置盾构隧道结构的土层的回弹值。

3)当地下水位线上升到盾构隧道拱底标高、中心标高、拱顶标高位置时，盾构隧道结构会出现相应的上升位移和边壁的侧向位移，并且位移值会随着水位的上升越来越大，同时隧道发生的结构变形也越来越大。对于直线段的隧道结构，如果其下方土层较均匀，当地下水整体上升时，直线段的隧道发生整体上浮，并且不会产生不均匀的位移。

由于盾构隧道所在土质物理条件的复杂性与水土的相互作用，本文采用的模拟方法不可避免地采取一些假设和简化。但文中的计算结果能够揭示出地下水位上升到不同位置时对盾构隧道位移变化的影响规律，所获得的规律性认识对同类工程具有较好的参考价值，对地下水位升高后的盾构隧道变形监测与内力控制具有一定的理论价值与现实指导意义。

需要注意的是，文中所建立的有限元模型仅适用于地下水位上升后对盾构隧道引起的上浮变形问题。当地下水位下降时，在降水过程中，土体的有效应力会增加，盾构隧道的沉降量会增加，此时需要采用渗流耦合的有限元分析方法来计算。

目前地下水位变化对盾构隧道在施工过程中所带来的影响尚未展开研究，因此在今后的理论研究中，应对此进行研究，进而揭示出盾构在施工时受到地下水位升降的影响规律，这也是笔者下一步的主要研究方向。

［1］ 职洪涛，路明鉴，杜守继.盾构隧道通缝拼装管片上浮的数值模拟分析［J］.地下空间与工程学报，2007(S2):98 －101.(ZHI Hongtao，LU Mingjian，DU Shouji.Numerical simulation analysis on rising displacement for shield tunnel segment with straight joint［J］.Chinese Journal of Underground Space and Engineering，2007(S2):98 － 101.(in Chinese))

［2］ 叶飞，朱合华，丁文其.基于弹性地基梁的盾构隧道纵向上浮分析［J］.中国铁道科学，2008(4):67－71.(YE Fei，ZHU Hehua，DING Wenqi.Longitudinal upward movement analysis of shield tunnel based on elastic foundation beam［J］.China Railway Science，2008(4):67 － 71.(in Chinese))

［3］ 叶飞，朱合华，丁文其，等.大断面盾构隧道施工抗浮计算研究［J］.地下空间与工程学报，2007(5):67－71.(YE Fei，ZHU Hehua，DING Wenqi，et al.Analysis on antibuoyancy caculation in excavation of big cross-section shield tunnel［J］.Chinese Journal of Underground Space and Engineering，2007(5):67 －71.(in Chinese))

［4］ 林志斌，李元海，赵耀强，等.地下水对软土盾构隧道施工的影响规律分析［J］.地下空间与工程学报，2012(2):157 －163，171.(LIN Zhibin，LI Yuanhai，ZHAO Yaoqiang，et al.Numerical analysis on the impact of groundwater on shield tunnel construction under soft soil［J］.Chinese Journal of Underground Space and Engineering，2012(2):157 －163，171.(in Chinese))

［5］ 李昀，张子新，张冠军.泥水平衡盾构开挖面稳定模型试

验研究［J］.岩土工程学报，2007(7):123 －128.(LI Yun，ZHANG Zixin，ZHANG Guanjun.Laboratory study on face stability mechanism of slurry shields［J］.Chinese Journal of Geotechnical Engineering.2007(7):123 －128.(in Chinese))

［6］ 张飞进，高文学.盾构隧道沉降影响因素分析与施工优化［J］.北京工业大学学报.2009，35(5):51 －55.(ZHANG Feijin，GAO Wenxue.Shield tunnel subsidence influence factor analysis and construction optimization［J］.Journal of Beijing University of Technology，2009，35(5):51 －55.(in Chinese))

［7］ 朱忠隆，张庆贺，易宏伟.软土隧道纵向地表沉降的随机预测方法［J］.岩土力学，2001，22(1):57 －60.(ZHU Zhonglong，ZHANG Qinghe，YI Hongwei.Stochastic theory for predicting longitudinal settlement in soft-soil tunnel［J］.Rock and Soil Mechanics，2001，22(1):57 － 60.(in Chinese))

［8］ 施成华，彭立敏.随机介质理论在盾构法隧道纵向地表沉降预测中的应用［J］.岩土力学，2004，25(2):153 －156.(SHI Chenghua，PENG Limin.Application of stochastic medium theory to predicting settlement in longitudinal surface due to tunnel construction by shield［J］.Rock and Soil Mechanics，2004，25(2):153 －156.(in Chinese))

［9］ 魏纲，徐日庆.软土隧道盾构法施工引起的纵向地面变形预测［J］.岩土工程学报，2005，27(9):106 －110.(WEI Gang，XU Riqing.Prediction of longitudinal ground deformation due to tunnel construction with shield in soft soil［J］.Chinese Journal of Geotechnical Engineering，2005，27(9):106 －110.(in Chinese))

［10］ Chungsik Y.Finite-element analysis of tunnel face reinforced by longitudinal pipes［J］.Computers and Geotechnics，2002，29(1):73 －94.