两个水平密贴地下结构的地震响应分析

陈建民，项彦勇

(北京交通大学土木建筑工程学院，北京 100044)

0 引言

随着城市的快速发展，城市交通日益拥堵，以地下铁道为骨干的大运量快速公共交通系统已经成为改善城市交通的最佳途径。近几年来我国大力发展地下铁道，以北京为例，北京市在2009年地铁4号线开通运营以后，运营总里程达到230 km，2010年达到300 km，2015年将形成三环、四横、五纵、七放射，总长561 km的轨道交通网络。地下空间的不断开发和利用，必将导致城市地下空间日趋紧张，地下结构相互紧邻的情况就会出现，如上海地铁9号线一期工程西出入段(九亭站—七宝站)三线并行的区间隧道最小净距为3.8 m;广州市市民广场站至天河南一路站区间隧道近距离下穿地铁1号线体育西站至体育中心站区间隧道，上、下隧道的最小净距为2.342 m;南京地铁1号线与玄武湖公路隧道底板的上、下最小净距仅为1.004 m［1－3］。以上类似的情况在我国的大中城市出现的概率将会越来越大。另外，由于地下结构抗震研究工作开展不足，目前我国还没有独立的地下结构抗震设计规范。长期以来，地铁结构的抗震设计基本是参照《铁路工程抗震设计规范》［4］和《建筑抗震设计规范》［5］进行。相关的抗震设计规范对2个或2个以上的邻近地下结构群均未给出相关的规定。因此，有必要对相互邻近的地下结构的地震响应特征进行研究。

对相互邻近的地下结构的地震响应问题，国内外已有学者采用解析法和数值法进行了一些研究，并初步探讨了影响邻近地下结构动力响应的主要因素包括入射地震波频谱、邻近地下结构的间距、土层性质、地下结构的形状和地下结构的埋深等。20世纪70年代初，Pao等［6］采用波函数展开法，开创性地研究了无限空间中单个洞室在弹性波入射下的动应力集中问题。随后，Lee等［7］研究了半无限空间中单个洞室对SH波的散射问题。Balendra等［8］采用镜像法，研究了半无限空间中不同间距下的衬砌双隧道在SH波作用下的动应力集中，并发现2个隧道之间存在相互作用。梁建文等［9］采用波函数展开法，给出了地下双洞室在平面波SV波入射下动力响应二维问题的一个解析解，研究表明2个距离较近洞室之间的相互作用对地下双洞室的动应力集中具有显著的放大作用。以上都是采用解析法得到的研究成果。由于实际工程中地下环境极其复杂，如不均匀的场地地质、不规则的地下结构、随机的地震波等，采用数值法更具有实用性。庄海洋等［10］采用有限元软件ABAQUS对南京双洞地铁区间隧道的非线性地震反应特征进行了数值模拟，给出了隧道结构最大动应力的位置。陈磊等［11－13］分别对南京的双层竖向重叠地铁隧道和双层交叉地铁隧道的地震反应特征进行了数值模拟，研究表明邻近的2个隧道结构的地震响应存在着相互影响的关系。

综上所述，现有邻近地下结构的地震响应研究主要有以下特点:1)计算模型以二维模型居多;2)地下结构形式单一，以圆形隧道为主;3)地层假定为均质，地震荷载单一;4)洞室群存在一定的间距，没考虑密贴结构的情况。随着地铁的大规模建设，多个地下结构相互邻近的情况日益增多，地震响应研究具有重要的工程应用价值和社会、经济效益。本文以北京某新建地铁车站结构和上部密贴的既有公路隧道结构为对象，采用有限元分析软件MIDAS-GTS，对水平密贴地下结构的地震响应进行数值模拟，分析公路隧道结构在有、无地铁车站结构时的地震响应，探讨接触面性质对水平密贴结构地震响应的影响。

1 计算模型

1.1 工程概况

水平密贴的两个地下结构计算模型如图1所示。上部为既有公路隧道结构，下部为新建地铁车站结构，两者密贴。公路隧道是一个四跨单层的矩形混凝土结构，高为9.70 m，总宽度为 48.90 m，顶板厚度为 1.40 m，底板厚度为1.30 m，侧墙厚度为1.30 m，隔墙厚度均为0.80 m，两层三跨岛式地铁车站的横断面尺寸为23.50 m ×16.88 m，顶板和底板厚度均为 1.85 m，侧墙厚度为1.00 m，钢管柱的直径为0.9 m。

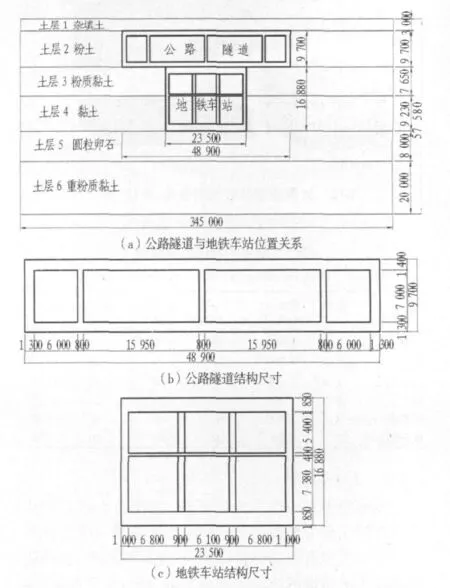
图1 计算模型的尺寸(单位:mm)Fig.1 Dimensions of calculation model(mm)

1.2 有限元模型

采用MIDAS-GTS软件进行数值计算，土体采用实体单元和摩尔－库仑本构模型，地铁车站结构和公路隧道结构都采用实体单元和线弹性本构模型。

为了减小计算范围和人工边界对结构地震反应的影响，选择不同计算范围的数值模型进行了试算，发现当土体横向计算范围(X轴方向模型边界至公路隧道结构边缘的距离)取公路隧道结构宽度的3倍时，计算精度已能满足要求。取模型宽度为公路隧道结构宽度的7倍。三维模型区域为345 m×42 m×57.58 m，有限元网格如图2所示(按刚度等效和质量等效原则，把直径为0.9 m的钢管柱等效为1.0 m×1.0 m的矩形混凝土柱)。

1.2.1 模型材料参数

公路隧道结构为C30混凝土，重度为25 kN/m3，弹性模量为30.0 MPa，阻尼比为5%;地铁车站结构为C40混凝土，重度为25 kN/m3，弹性模量为32.5 MPa，阻尼比为5%。地层分布和材料的物理力学参数如表1所示。

图2 计算模型有限元网格图(单位:m)Fig.2 FEM mesh of calculation model(m)

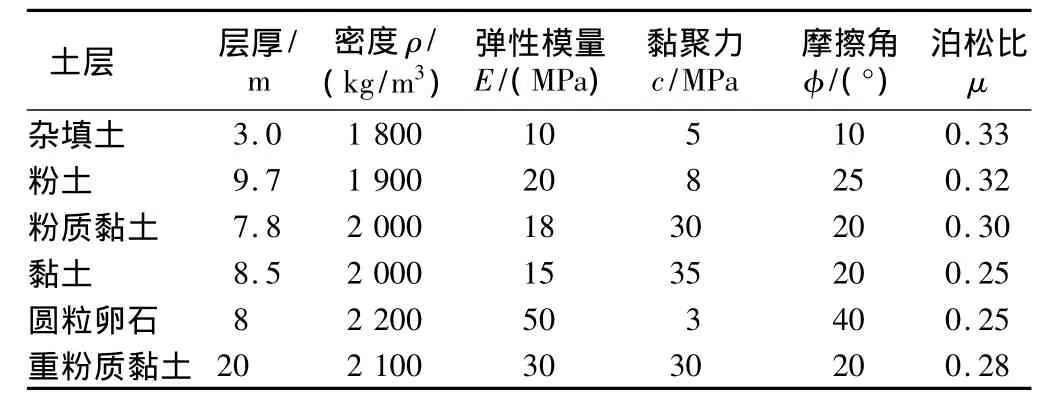
表1 地层的物理力学参数Table 1 Physical and mechanical parameters of ground

1.2.2 人工边界

实际场地是一个半无限区域，但在对土体－结构进行有限元动力分析时，土体的计算范围只能是有限的。对于范围有限的计算区域，在地震激励下，波动能量将在人工截取的边界上发生反射，使波发生震荡，导致模拟失真。为了解决有限截取模型边界上波的反射问题，可以引入人工边界条件，如黏性边界［14］、旁轴近似边界［15］、透射边界［16］、黏弹性边界［17］等。本文采用Deeks［17］提出的黏弹性边界，在模型边界施加与地层性质对应的线性弹簧和阻尼，以考虑模型边界地层的弹性恢复和对散射波的吸收。弹簧常量

式中:k0=Eα/30(E为土体的弹性模量;α为修正系数，一般取1.0);Ai为土层垂直于i坐标轴的截面面积。

阻尼系数:

式中:Aj为边界节点j所对应的面积;cpj和csj分别为压缩波和剪切波的单位面积阻尼常数。

式中:λ=uE/(1+u)(1－2u);G=E/2(1+u);ρ为材料的密度;u为泊松比。

利用表1所示的地层材料参数，由式(1)—(5)计算，得到弹簧常量和阻尼系数如表2所示。

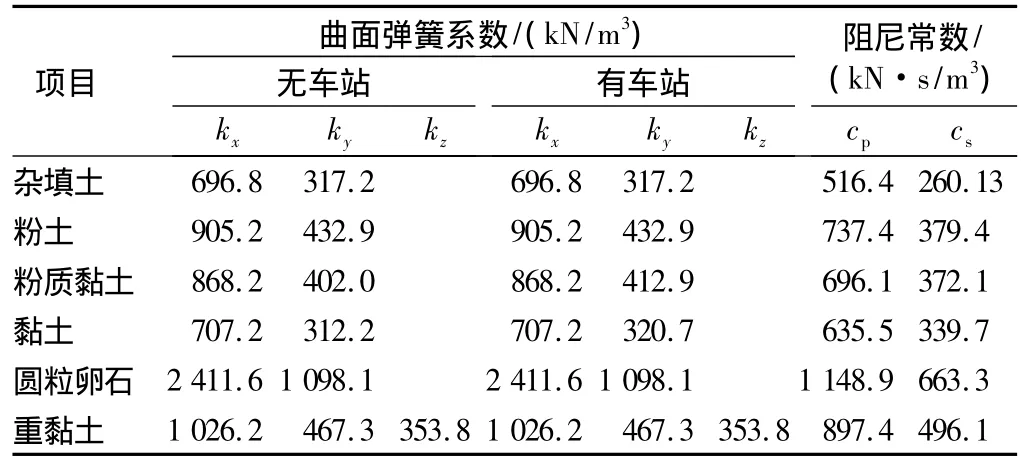
表2 弹簧常量与阻尼系数Table 2 Spring stiffness and damping coefficient

1.2.3 隧道结构与地铁车站结构接触面的模拟方法

由于地铁车站顶板直接与公路隧道底板接触，两个结构之间存在接触面，垂直接触面方向可视为刚性连接，水平方向则是一个摩擦接触面，该接触面采用Goodman单元模拟。接触面的法向采用“硬接触”，即法向刚度取很大的数值;接触面的切向服从Coulomb摩擦定律，切向刚度ks按经验公式确定，取接触面周围“最硬”相邻区域的等效刚度的10倍［18］，即

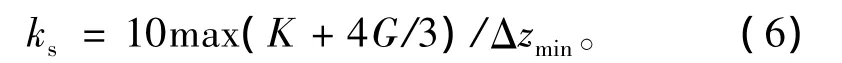
式中:K=E/3(1－2u);Δzmin是接触面法向方向上连接区域的最小尺寸(见图3)。计算模型的 Δzmin为0.65 m，由式(6)求得切向刚度 ks=5.5 ×108kPa。

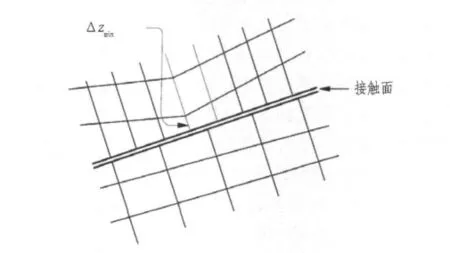
图3 接触面法向方向上连接区域的最小尺寸Fig.3 Minimum dimension of connection zone in the normal direction of an interface

1.2.4 地震荷载

根据GB 50011—2010《建筑抗震设计规范》，选取设计地震分组为第1组，抗震设防烈度为8度，设计基本地震加速度值为0.20 g。由于缺少场地的实测数据，首先选用国际常用的EL-Centro地震波作为基本波形，然后进行处理使其符合场地条件，得到的地震波加速度时程和反应谱如图4所示。对于地下结构的动力响应研究，地震荷载的输入在通用有限元软件中的实现方式主要有2种:1)通过直接在模型底板施加加速度或速度荷载的方式实现;2)通过在人工边界上施加等效节点荷载的方式实现。本模型采用在模型底部输入地震加速度的方式，地震加速度的激励方向为与水平面平行且垂直于公路隧道轴线的方向。

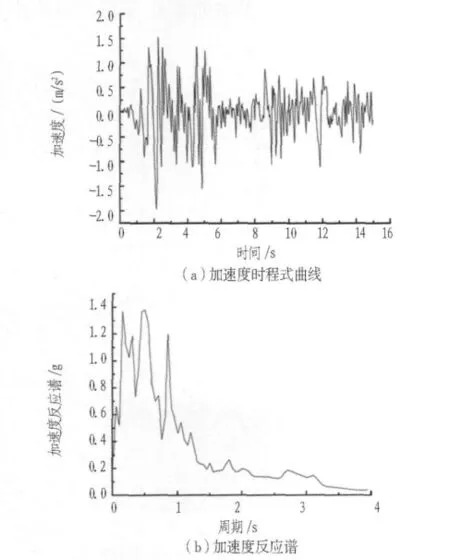
图4 El-Centro波加速度时程与反应谱Fig.4 Time-history and response spectrum of acceleration of El-Centro wave

2 计算结果与分析

图5所示为计算结果观察节点的位置图。观察节点位于隧道轴线方向中间位置的A－A平面上，沿隧道轴线方向该平面距离模型边界21 m。

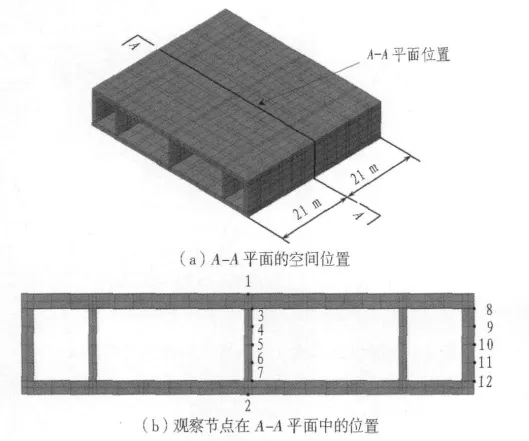
图5 观察节点布置图Fig.5 Layout of observation points

2.1 公路隧道结构水平位移响应

图6所示为在水平El-Centro波作用下公路隧道顶板、底板的水平位移反应以及相对水平位移。从图中可以看出:1)地铁车站对公路隧道结构的水平位移影响不明显，影响幅度在5%以内，无地铁车站时公路隧道顶板、底板的水平位移峰值分别为39.5 mm和38.9 mm，有地铁车站时公路隧道顶板、底板的水平位移峰值分别为39.3 mm和38.3 mm。2)公路隧道结构在地震波动力作用下的相对位移比较小;但地铁车站的存在对公路隧道结构相对水平位移具有放大的影响，最大值的放大幅度约为20%。

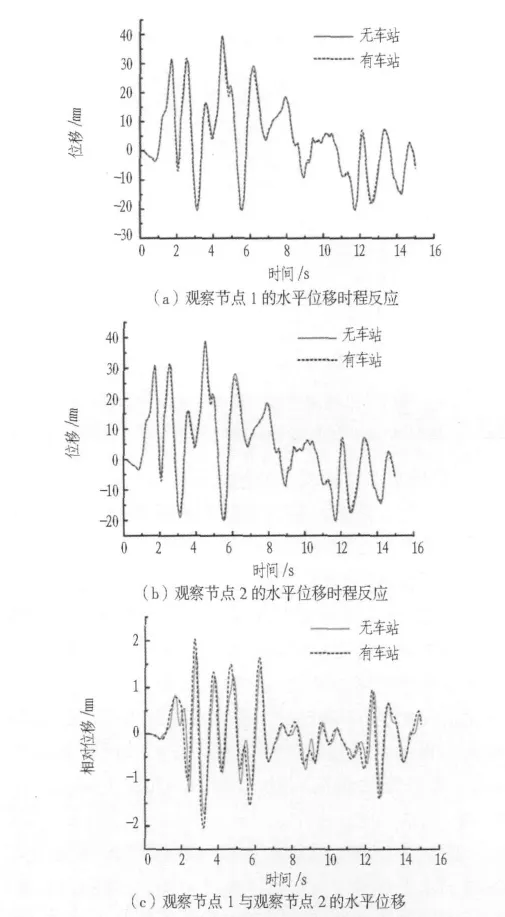
图6 隧道结构顶板与底板水平位移时程反应Fig.6 Time-history curves of horizontal displacement of roof slab and bottom slab of tunnel

图7所示为公路隧道结构隔墙和侧墙的相对水平位移。从图中可以看出:1)在地震波作用下隧道墙体的相对水平位移随墙体高度增大而增大。2)公路隧道墙体在有地铁车站时的相对水平位移明显大于无地铁车站时的相对水平位移，说明了地铁车站结构的存在对公路隧道结构的相对位移具有放大作用，这将会增大公路隧道结构的内力，对隧道结构的抗震不利。

图7 公路隧道结构墙体相对水平位移Fig.7 Relative horizontal displacement of side wall of highway tunnel

2.2 公路隧道结构水平加速度反应

图8为公路隧道结构顶板和底板在有、无地铁车站时的水平加速度时程曲线图。由图可知:1)在没有车站时，公路隧道顶板的水平加速度峰值大于隧道底板的峰值，而在有车站时相反。2)地铁车站对公路隧道结构水平加速度反应具有放大作用。公路隧道顶板的水平加速度峰值在无车站情况时为1.76 m/s2，在有车站情况时为1.86 m/s2，放大幅度约为5.7%;公路隧道底板的水平加速度峰值在无车站情况时为1.71 m/s2，在有车站情况时为1.87 m/s2，放大幅度约为9.4%。

图9为公路隧道结构顶板和底板在有、无地铁车站时的水平加速度反应谱。由图可知，公路隧道顶板、底板水平加速度反应谱同样也验证了地铁车站对公路隧道结构的水平加速度反应具有放大作用。

2.3 公路隧道结构动应力分析

图10给出了在水平方向的El-Centro波作用下有、无地铁车站时公路隧道结构A－A剖面处的Mises应力分布云图。由图可知:1)公路隧道结构动应力分布特征在有、无车站结构时存在一些相同点。例如，墙－板连接处的动应力值较大，公路隧道墙体结构的动应力值比隧道顶板和底板结构动应力值大。2)在有车站结构时，公路隧道结构动应力分布特征发生了明显的改变。①公路隧道结构的动应力明显增大，隔墙和底板最为突出;②中间隔墙顶部的应力最大值略微减小(约为1.2%)，但中间隔墙底部的应力值最大值增大了约11.3%;③靠近地铁车站侧墙周边的公路隧道底板结构的动应力有明显的增大，动应力最大值增大了约2.5倍。

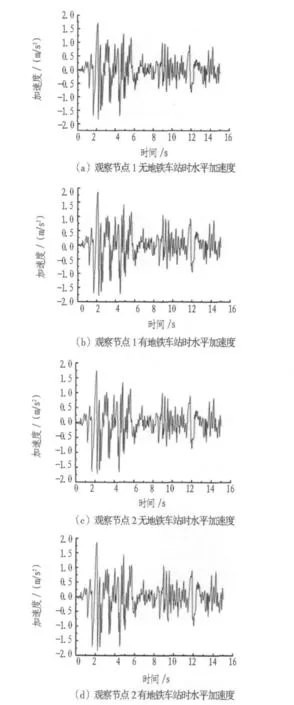
图8 公路隧道顶板与底板水平加速度时程曲线Fig.8 Time-history curves of horizontal acceleration of roof slab and bottom slab of highway tunnel

2.4 两个结构之间的接触面性质对公路隧道结构地震响应的影响

假设按不同的接触面性质进行试算，发现接触面性质对公路隧道结构地震响应的主要影响因素为接触面的切向刚度。为此，选取 ks=0，ks=1×106kPa，ks=1×1012kPa 3种不同的切向刚度分别进行计算，分析接触面切向刚度值的影响。

图9 公路隧道顶板与底板水平加速度反应谱Fig.9 Response spectrum of horizontal acceleration of roof slab and bottom slab of highway tunnel

对比分析发现，不同切向刚度值对公路隧道结构的水平位移和水平加速度的影响幅度均小于0.1%，但对公路隧道结构的动应力影响显著。图11为公路隧道结构A-A剖面处的Mises应力分布云图。由图可知:当切向刚度ks=0时，隧道结构的最大动应力值为588.2 kPa;当切向刚度ks=1×106kPa时，隧道结构的最大动应力值为587.9 kPa;当切向刚度ks=1×1012kPa时，隧道结构的最大动应力值为583.9 kPa。由此可见，公路隧道结构的动应力最大值都出现在中间隔墙的底部，并且随切向刚度的增大而减小。

不同的切向刚度值对公路隧道结构底板的动应力影响比较明显，尤其是对接触面范围内的公路隧道结构底板。当接触面的切向刚度增大时，地铁车站顶板与公路隧道底板之间的联系增强，趋于整体化，共同工作。因此，随着接触面切向刚度的增大，接触面范围内的公路隧道底板下侧的动应力逐渐减小，而接触面两侧的公路隧道底板的动应力却有明显的增大。

3 结论与讨论

本文利用有限元软件MIDAS-GTS，根据设定条件下的计算与分析，主要结论有4点。

图10 有、无地铁结构公路隧道结构A－A剖面处的Mises应力分布云图(单位:kPa)Fig.10 Cloud of distribution of Mises stress at A-A cross-section of highway tunnel with and without Metro station(kPa)

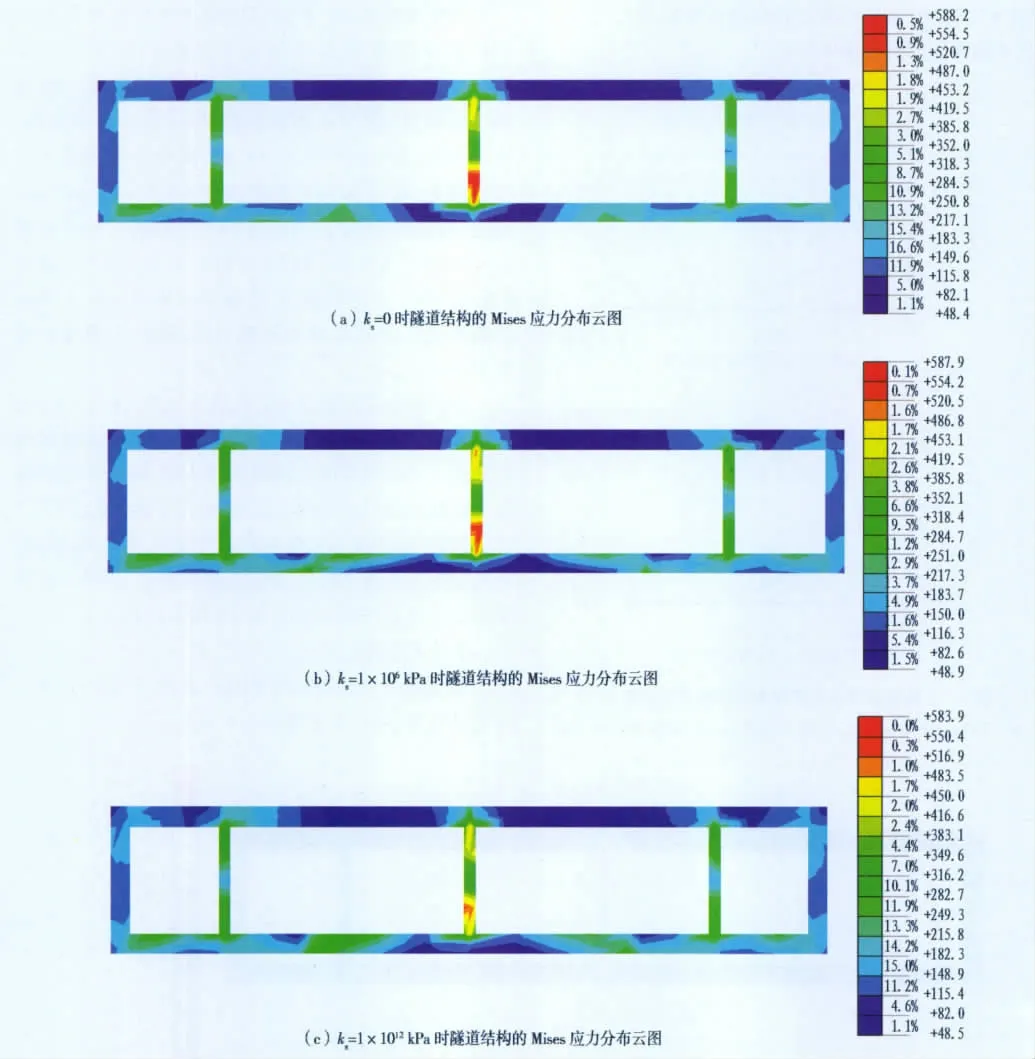
图11 不同切向刚度时公路隧道结构A－A剖面处的Mises应力分布云图(单位:kPa)Fig.11 Cloud of distribution of Mises stress at A-A cross-section of highway tunnel under different tangential rigidities(kPa)

1)新建地铁车站对既有公路隧道结构的水平位移影响不明显，影响幅度在5%以内。公路隧道结构相对水平位移比较小，地下结构在地震作用下的位移主要表现为结构的整体位移，自身变形比较小。地铁车站结构使公路隧道结构相对水平位移增大，水平相对位移峰值增大幅度约为20%。

2)公路隧道结构在有、无地铁车站结构情况下的水平加速度反应时程曲线形态相似。地铁车站结构对公路隧道结构的水平加速度响应具有放大作用，隧道顶板的水平加速度响应峰值放大幅度约为6.3%;隧道底板的水平加速度响应峰值放大幅度约为8.7%。

3)在地铁车站结构的影响下，公路隧道结构的动应力分布特征发生了明显的改变:动应力明显增大，隔墙和底板最为突出;中间隔墙顶部的应力最大值略微减小(约为1.2%)，中间隔墙底部应力最大值增大了约11%;靠近地铁车站侧墙周边的公路隧道底板结构的动应力明显增大(增大了150%左右)。

4)结构接触面性质对公路隧道结构的动力响应有影响，主要影响因素是结构接触面的切向刚度。切向刚度对公路隧道结构水平位移和水平加速度的影响幅度均小于0.1%。不同的切向刚度值对公路隧道结构底板的动应力影响比较明显，尤其是对接触面范围内的公路隧道结构底板。随着接触面切向刚度的增大，接触面范围内的公路隧道底板下侧的动应力减小，而接触面两侧的公路隧道底板的动应力却有明显的增大。

当前，对两个水平密贴结构地震响应的影响研究不多，相关的震害调查和理论研究的资料较少。在今后研究中应考虑地震波特性、土层状况、结构埋深、结构形状等影响因素，进行更深入地研究，得出有运用意义的理论和提出具体的抗震措施，为制定地下结构抗震规范提供参考。

［1］ 陈越峰，张庆贺，张颖，等.近距离三线并行盾构隧道施工实测分析［J］.地下空间与工程学报，2008，4(2):335－340.(CHEN Yuefeng，ZHANG Qinghe，ZHANG Ying，et al.In-situ monitoring and analyzing on construction of three closely spaced parallel pipe shield tunnels［J］.Chinese Journal of Underground Space and Engineering，2008，4(2):335 －340.(in Chinese))

［2］ 张凯，贺婷.盾构近距离下穿地铁运营隧道施工技术［J］.隧道建设，2008，28(4):483 － 488.(ZHANG Kai，HE Ting.Construction technology for shield-bored tunnel crossing underneath adjacent operation Metro tunnel［J］.Tunnel Construction，2008，28(4):483 －488.(in Chinese))

［3］ 李围，何川.盾构隧道近接下穿地下大型结构施工影响研究［J］.岩土工程学报，2006，28(10):1277 －1282.(LI Wei，HE Chuan.Study on construction influence of shield tunnels traversing adjacently under underground large-scale structure［J］.Chinese Journal of Geotechnical Engineering，2006，28(10):1277 －1282.(in Chinese))

［4］ 中华人民共和国国家标准.GB 50111—2006铁路工程抗震设计规范［S］.北京:中国计划出版社，2009.

［5］ 中华人民共和国国家标准.GB 50011—2010建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［6］ Pao Y H，Mow C C.Diffraction of elastic waves and dynamic stress concentrations［M］.New York:Crane，Russak ＆Company Inc.，1973.

［7］ Lee V W，Trifunac M D.Response of tunnels to incident SH-waves［J］.Journal of Engineering Mechanics，ASCE，1979，105:643 －659.

［8］ Balendra T，Thambiratnam D P，Koh C G，et al.Dynamic response of twin circular tunnels due to incident SH-waves［J］.Earthquake Engineering and Structural Dynamics，1984，12:181－201.

［9］ 梁建文，张浩，Vincent W Lee.地下双洞室在SV波入射下动力响应问题解析解［J］.振动工程学报，2004，17(2):16 － 24.(LIANG Jianwen，ZHANG Hao，Vincent W Lee.An analytical solution for dynamic stress concentration of underground twin cavities due to incident SV waves［J］.Journal of Vibration Engineering，2004，17(2):16 － 24.(in Chinese))

［10］ 庄海洋，陈国兴.双洞单轨地铁区间隧道非线性地震反应分析［J］.地震工程与工程振动，2006，26(2):133－139.(ZHUANG Haiyang，Chen Guoxing.Analysis of nonlinear earthquake response of Metro double-tunnels［J］.Earthquake Engineering and Engineering Vibration，2006，26(2):133 －139.(in Chinese))

［11］ 陈磊，陈国兴.近断层强地震动下双层竖向重叠地铁隧道的地震反应［J］.防灾减灾工程学报，2008，28(4):5－14.(CHEN Lei，CHEN Guoxing.Seismic response of vertically double-layered metro tunnels under near-fault strong ground motion［J］.Journal of Disaster Prevention and Mitigation Engineering，2008，28(4):5 －14.(in Chinese))

［12］ 陈磊，陈国兴，李丽梅.近场和远场地震动作用下双层竖向重叠地铁隧道地震反应特性［J］.中国铁道科学，2010，31(1):81 － 88.(CHEN Lei，CHEN Guoxing，LI Limei.Seismic response characteristics of the double-layer vertical overlapping metro tunnels under near-field and farfield ground motions［J］.China Railway Science，2010，31(1):81 －88.(in Chinese))

［13］ 陈磊，陈国兴，龙慧.地铁交叉隧道近场强地震反应特性的三维精细化非线性有限元分析［J］.岩土力学，2010，31(12):280 － 285，292.(CHEN Lei，CHEN Guoxing，LONG Hui.3D refined nonlinear finite element analysis of intersecting Metro tunnels under near-field ground motion［J］.Rock and Soil Mechanics，2010，31(12):280 －285，292.(in Chinese))

［14］ Lysmer J，Kulemeyer R L.Finite dynamic model for infinite media［J］.Journal of the Engineering Mechanics，ASCE，1969，95(4):859 －877.

［15］ Clayton R，Engquist B.Absorbing boundary conditions for acoustic and elastic wave equations［J］.Bulletin of the Seismological Society of America，1977，67(6):1529 －1540.

［16］ 廖振鹏，黄孔亮，杨柏坡，等.暂态波透射边界［J］.中国科学:A辑数学 物理学 天文学 技术科学，1984(6):76－84.

［17］ Deeks A J，Randolph M F.Axisymmetric time-domain transmitting boundaries［J］.Journal of the Engineering Mechanics，1994(1):25 －42.

［18］ 陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例［M］.北京:中国水利水电出版社，2009.