基于油中溶解气体分析的变压器故障诊断

孙洁，邢九霞

(河北联合大学电气工程学院，河北唐山 063009)

0 引言

变压器是一种静止的电器设备，是电力系统中最重要的设备之一，在国民经济其它部门也获得了广泛的应用。变压器运行状况直接决定电力系统运行的安全，稳定和供电可靠性。通过对电力变压器运行过程中的故障诊断，及时有效的判断其状态，将使变压器长期、安全可靠的运行成为可能。因此加强对电力变压器内部故障诊断方法的研究，提出更有效地检测和诊断变压器潜伏性故障或缺陷的方法具有十分重要的现实意义。

变压器智能化诊断方法主要有:(1)基于人工神经网络的变压器故障诊断，但是由于神经网络自身结构的特点，其收敛速度比较慢，收敛精度不理想，甚至不收敛且易陷入局部极小。(2)以DGA为特征量的模糊综合诊断模型及方法，由于模糊数学研究是“内涵明确，外延不明确”的对象，因此存在隶属函数难以确定的缺点(3)以DGA为特征量的故障诊断专家系统，它也存在不少缺陷，如知识获取的瓶颈问题、推理单调性以及自学习困难等许多技术问题。

鉴于以上方法的种种弊端，本文引入思维进化算法优化神经网络的连接权值，深入分析改进的椭球基函数神经网络信息融合的变压器故障诊断方法，比较验证本方法的有效性、可行性和优越性。

1 改进的椭球基神经网络及其结构

经典椭球基函数神经网络有可能导致权值调整不稳定，网络不收敛，模式识别能力严重下降。因此鉴于上述情况，本文对经典椭球基函数神经网络稍作改进，隐层神经元与输出神经元进行全连接，最后通过对隐含层输出数据的线性加权求和得到网络的最终输出。改进的椭球基函数神经网络模型结构图如图1所示:

其中Zj为超椭球各维上的初始半轴长。

图1中Wsj为第S个输出神经元与第j个隐层单元之间的连接权值，以椭球基单元j为例，则其相应输入netjin可以表示为:隐层神经元j的输出可以表示为:

图1 改进的椭球基函数神经网络模型结构图

椭球单元的输入范围:(－∞，1]，输出范围:(0，1]。当输入样本值与椭球中心重合时，椭球输出为1;当样本值在椭球内且逐渐远离中心时，椭球单元输出值逐渐减小;当样本数据值在椭球上时，椭球单元输出值为 ( eβ+1)/2eβ，而当样本数据值在椭球外时，则随着其值远离椭球中心，椭球单元输出值迅速趋于0。

以椭球基函数神经网络的第S个输出神经元为例，其输出可以表示为:

即输出层神经元的输出为隐层神经元输出的线性加权和。

2 思维进化算法优化网络权值

为了使椭球基函数神经网络达到期望的输出，必须采取有效地方式算法对其进行训练。从椭球基函数神经网络的结构模型着手，可以发现该神经网络中需要训练优化的参数主要有三个，即:椭球单元在输入向量各维上的中心，椭球单元在输入向量各维上的半轴长以及隐含层与输出层之间的连接权值。本课题只研究隐含层与输出层的连接权值的优化，经分析本文决定采用思维进化算法训练得到隐含层与输出层之间的连接权值。

思维进化优化神经网络权值的流程图如图2:

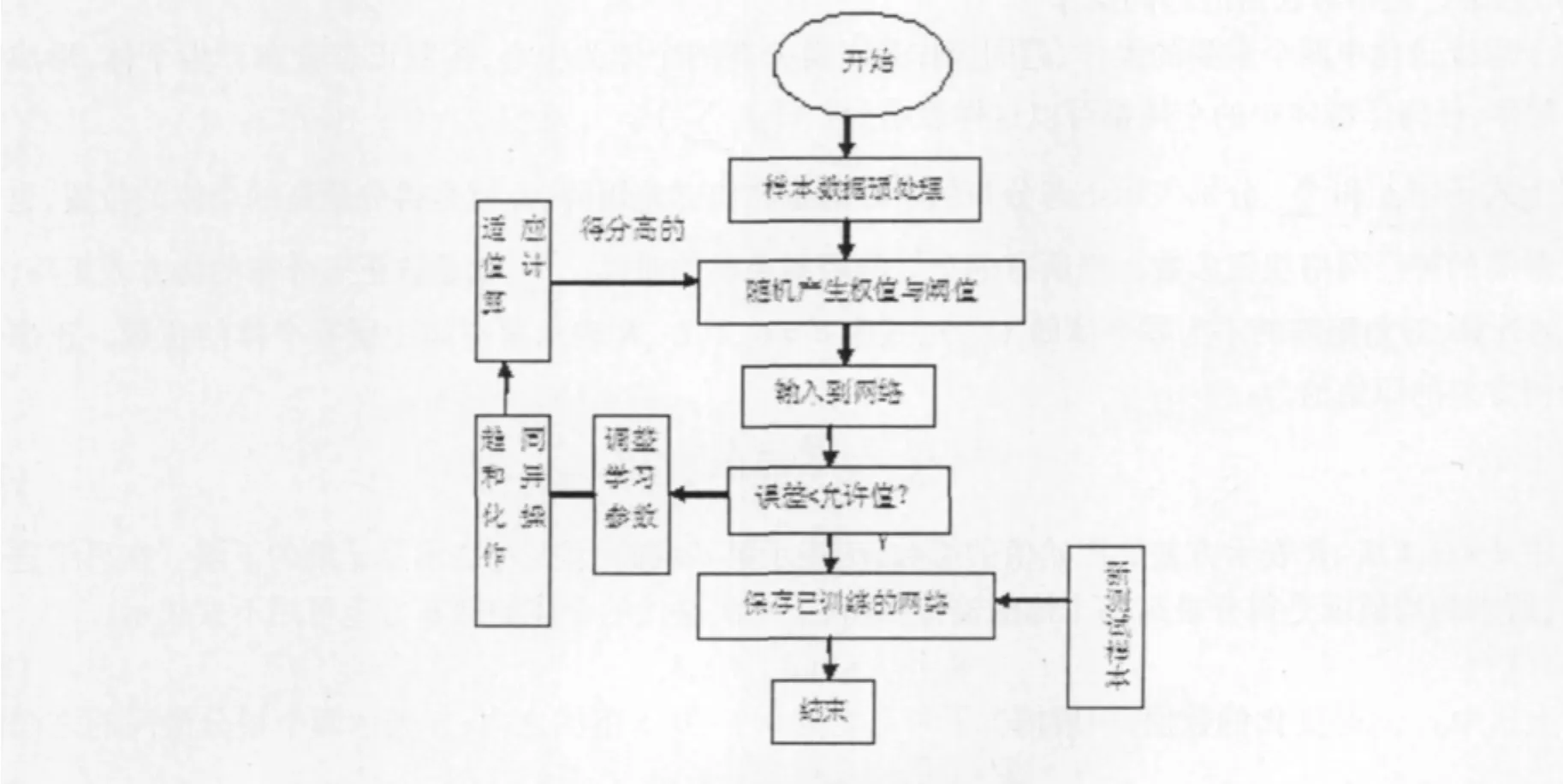
图2 思维进化优化神经网络的流程图

主要计算流程有以下几个方面:

(1)思维进化初始群体的生成

假设一个神经网络，有n个中间层，每一个中间层最大神经元数为m。对于神经网络来说一旦确定了中间层数和中间层的神经元数，神经网络的结构也定了。随意的出现N个即为思维进化的初始结构群体，任何一个数中有n个数值，那么也就是个体结构，在思维进化算法中，每个个体都是从中间层神经元个数0，1，...，m中选择。比如(a1，a2…，ai，… ，an)表示第一个中间层神经元为a1，第二个中间层的神经元a2，…，第n个中间层神经元为an，构成这样神经网络结构。在神经网络中，j－1=0，1，…，m代表中间层神经元的个数，i=1，2，…n代表中间的层个数;任何一个中间层现有的神经元数的得分可以用(bi1，bi2，…，bij，…，bi(m+1))来表达，bij表示在第i个中间层有神经元数位j－1。有了这些已知条件，思维进化中的个体得分就可以用下边的式子来表示:

思维进化中的公告板中可以记录矩阵里神经元的信息，神经元数0，1，2，…，m，也就是Cj=j－1，在思维进化算法，矩阵中每个位置的参数都是随机产生的。

(2)思维进化算法的适应度函数

思维进化算法选择的适应度函数为:

式中yi是代表的神经网络实际得到的值，ti是神经网络里理想的输出，n为一共选取的数值的个数。

(3)思维进化算法得分高的子群体的优化

在解空间内随机的产生N组随机数，作为初始权值的群体，每组中个数是权值的个数，按照式(4)计算每个个体的得分，分数由高到低排序，从中选择前M+T个个体作为优胜个体，则每个个体的大小定义为:

(4)思维进化中对权值的趋同操作

对于思维进化中两个重要的操作，趋同操作是以得分高的个体为中心，按照正态分布产生个体，形成M+T子群体，任何子群体中的个体都可以这样表示为:N(μ，∑)。

以上式子中μ和∑分别表示正态分布的中心向量和协方差矩阵。μ就是得分最高的个体的位置，也就是得分最高的神经网络权值参数。当所有的个体两两不关联的时候，∑就是该正态分布的协方差矩阵，经过i次的计算，对角矩阵的不为零个体即{δid}，式中d=O，1，L，R表示解空间中所有个体的位数。正态分布中任何方差的原始值为:

式中d=O，1，L，R表示方差的原始值的维数，Hd表示第d维的上限，Ld表示第d维的下限。在思维进化过程中，所求的均值就是得分最高的个体的连接权值，下一次迭代的个体的散布方差可用下式表示:

以上式中c1、c2是变化的数值，一般情况下可以定为0.1～0.5范围之内;δ表示两个得分最高的之间的位置差。

(5)思维进化中对权值异化操作

思维进化中异化操作的过程就是n个优胜子群体竞争全局优胜者的过程，本文寻优操作选用单纯形寻优。单纯形寻优就是在n+1个优胜个体组成的n维空间的一个单纯形，n+1个优胜个体分别记为X1，X2，X3，…，Xn，Xn+1，然后计算n+1个顶点的函数值并确定其中的最差点Xm，次差点Xs，最优点Xb，以及单纯形中除最差点外其余各点的形心Xm:

然后，过Xm求Xw的反射点Xr:

(6)思维进化算法中的收敛判别

判别是否满足收敛条件，如果不满足收敛条件则返回第4、5步继续进行趋同和异化操作，直到满足收敛条件为止。

3 改进的椭球基神经网络信息融合的建模

改进的椭球基神经网络也是一种前向网络，由输入层、隐含层和输出层三层构成。改进的椭球基函数神经网络和信息融合的具体实现方法是:用改进的椭球基函数神经网络融合得出初步的融合结果，将此结果进行归一化处理，将输出值作为证据理论识别框架上命题的基本概率分配，然后再应用组合规则进行综合诊断。图3是对变压器进行二次故障诊断的模型。

图3 变压器二次故障诊断模型

(1)本文一级融合采用CH4/H2，C2H4/C2H6和C2H2/C2H4三对比值归一化后作为神经网络的输入，归一化的方法是采用隶属度函数。隶属度函数表达式为:

所以输入神经元个数为3。将输出正常、低能放电、高能放电、中低温过热、高温过热五种情况做为一级融合的输出，则一级输出神经元个数为5。一级融合与二级融合隐含层均采用一层。

(2)二级融合的输入为一级融合的五种输出，输出为5种故障部位，即输出正常、穿心螺杆绝缘不良、铁心多点接地或匝间绝缘击穿、套管下端部或分接开关接触不良、引线接头断开或接触不良。

(3)隐含层个数经过多次试验以采取6个最佳。

(4)隐含层神经元的激活函数采用椭球基函数:

4 仿真试验

样本数据的选择对于网络的仿真实验事关重要，本文选取的数据样本如下表1:

表1 样本与故障状态对应表

将数据归一化后可得如下表2:

表2 归一化后输入样本与故障状态对应表

改进的椭球基神经网络训练过程的误差变化图如下:

图4 基于改进的椭球基神经网络训练过程的误差变化图

经过训练，改进的椭球基神经网路的是收敛误差最终稳定在4.6左右。

图5是思维进化算法的训练曲线。

图5 思维进化算法的训练曲线

5 结论

人工智能技术的融合可以补充单一技术的缺陷，从而可以更好的发挥每一种智能技术的优势，本文基于信息融合的变压器故障诊断与改进的椭球基神经网络结合建立模型，并运用思维进化算法优化权值，由仿真试验可以看出，它提高了神经网络的收敛速度，大大提高了变压器故障诊断的准确性，有很好的应用前景。

［1］孙承意;谢克明;程明琦，基于思维进化机器学习的框架及新进展［J］.太原工大学学报，1999:453-457.

［2］刘兆元.基于信息融合的大型电力变压器故障诊断［D］.济南:山东大学.2005.3

［3］Campbell A T，Coulson G.Information fusion for turbulence measurements in power physical application.Standardizing Lexical Resources，Maryland，USA，1999:69-75.

［4］李秀广.基于思维进化算法优化神经网络的变压器故障诊断［D］.太原:太原理工大学，2010.03.

［5］李俊杰.基于EBF神经网络的变压器内部故障诊断方法研究［D］.南京理工大学，2010.

［6］日罗菩，林树忠，詹湘琳.椭球基函数神经网络的指纹识别方法［［J］.计算机工程与应用，2008，44(34):219-222.

［7］E.A.Mohamed，A.Y.Abdela ZIZ.A Neural Network-based Seheme for Fault Diagnosi Power Transformers［J］.Eleetrie Power Systems Researeh，2005，75(2):29-39.

［8］谭敬波.基于油中溶解气体分析的电力变压器故障预测与诊断研究［D］.济南:山东大学，2009.10.

［9］杜文霞，吕锋，句希源.基于BP神经网络的电力变压器故障诊断［J］.变压器，2007，44(3):45-47.

［10］崔永学.基于油中溶解气体分析的变压器神经网络诊断系统研究［D］.天津:天津大学，2008.

［11］钱国超.大型电力变压器基于信息融合故障诊断技术的研究［D］.重庆大学，2008.