衰落信道下基于簇的协作频谱感知分析
陈万培,施 鹏,陈晓龙,范冠杰
(扬州大学信息工程学院,江苏扬州225009)
0 引言
分布式多用户合作检测中,融合中心通过各种算法将各认知用户的本地检测信息进行融合,获得更高的检测性能。文献[1,2]讨论了衰落信道下几种软合并分集算法能量检测的检测概率。文献[3]提出了一种适用于认知无线电的双门限能量检测算法。文献[4]提出了一种基于双门限本地检测信息汇报的合作检测方法,相比传统单门限本地检测上报方法可以大幅度减少受限信道上的上传比特开销。文献[5]推导分析了基于表决融合的协作频谱感知方法的感知性能,得出该算法在感知性能提高的同时可以节约大量比特开销。文献[6]提出了一种利用选择分集的基于簇理论的合作检测方法,相比于传统协作感知方法能获得更高的感知性能。文献[7]分析了基于簇理论的协作感知算法的感知性能。
这里首先分析了AWGN和Nakagami两种衰落信道下“与”规则融合协作感知的检测概率和归一化平均感知比特数,然后推导了当每簇中认知用户间的信道为Nakagami信道,且簇首和融合中心通过“与”准则融合本地检测信息时,基于簇理论的协作感知算法的检测概率和归一化平均感知比特数。仿真结果显示,基于簇理论的协作感知算法以消耗较多的比特开销为代价,能够获得更高的感知性能。
1 系统模型
在传统的决策融合分布式多用户合作检测中,各认知用户使用单门限能量检测算法做出是否存在主用户的本地决策,并上传至融合中心,由融合中心根据一定的判决规则对汇总后的融合信息进行最终判决。大量认知用户上报本地检测信息将占用大量信道带宽,在带宽受限的实际情况下,这里使用双门限本地检测信息上报的合作检测方法。各认知用户感知节点均设有2个门限λ0和λ1,当检测能量值Ei高于λ1时,主用户存在上传1;当Ei低于λ0时,主用户不存在上传0;而当检测能量值Ei介于这2个门限之间时,此检测节点认定为检测信息不可靠,不上传任何判决结果。本地频谱感知的判决结果yi表达式如下:
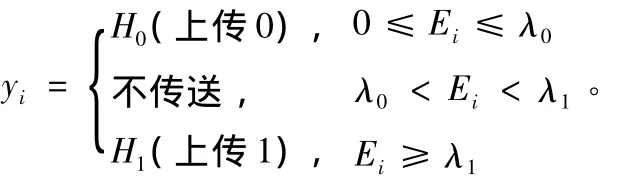
式中,H0为无效假设表示主用户不存在;H1为有效假设表示主用户存在。在该双门限合作检测方法中,本地认知用户只将足够可靠的判决信息向融合中心传送,大幅减少了受限信道上的上传比特开销。
2 性能分析
认知用户上报本地检测信息会产生一定的信令开销,而实际情况中报告信道通常带宽是受限的,用归一化平均感知比特数来衡量上传比特开销的大小。
设协作认知网络中共有N个认知用户感知节点,其中K个认知用户向融合中心报告了本地决策,则归一化平均感知比特数[4、5]为:

式中,Λ0=P{λ0<E<λ1H0}和Λ1=P{λ0<E<λ1H1}分别表示在H0与H1下不做判决的概率,而P0与P1分别为事件H0与H1出现的概率。
令Ω(λ)和Ψ(λ)分别为H0与H1情况下能量E的累积函数,表达式为:

那么Λ0和Λ1可以表示为Λ0=Ω(λ1)-Ω(λ0)和Λ1= Ψ(λ1)- Ψ(λ0)。
失败感知表示所有感知节点都没有向融合中心上报本地决策,δ0与δ1分别为H0与H1假设下的失败感知概率,其表达式为:

当有感知节点向融合中心上报本地决策,即成功感知(K≥1)的情况下,系统的虚警概率、检测概率和漏检概率分别为:
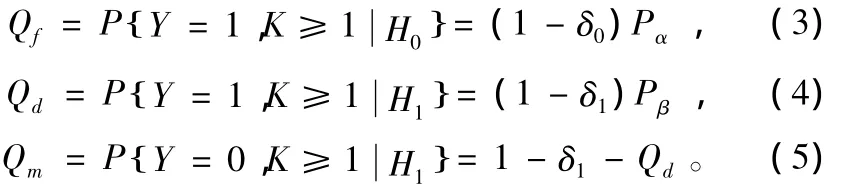
2.1 衰落信道下“与”融合
认知用户将本地检测信息上报给融合中心后,融合中心根据一定的判决规则,得出最终判定。常见的判决策略有“与”规则、“或”规则和K-outof-N规则。在“与”融合规则下,当所有上报本地决策的K个认知用户都做出主用户存在的判决H1,且其余N-K个认知用户都不上报本地决策时,融合中心才最终判决主用户存在。本节中融合中心使用“与”规则对上报信息进行汇总判决,以获得频谱资源利用率的最大化。
在实际通信环境中,认知用户和融合中心之间的信道是衰落信道,如式(2)所示,Ω(λ)与信噪比无关,所以衰落信道下Ω(λ)不变,δ0和Λ0也不变。假设所有的上传信道均为独立同分布的,且错误概率都为Pe。下面分别讨论在AWGN和Nakagami两种衰落信道下通过“与”规则对上报信息进行融合后的检测概率和平均感知比特数。
2.1.1 AWGN 信道下“与”融合
设Pe,i(i=1,2,…,K)为第i个认知用户和融合中心之间的传送信道,若每条信道都是独立同分布的,则Pe,i=Pe。AWGN信道下若使用BPSK调制方式,误码率为
在融合中心接收到认知用户上报的本地决策为0可能是以下2种情况:①认知用户上报的决策为0,在传送过程中没有受到信道衰落的影响,融合中心接收到的仍然是0;② 认知用户上报的决策为1,在传送过程中由于信道衰落的影响,使融合中心接收到的为0。由此可以得到高斯信道下“与”融合的Pα和Pβ如下:

将式(6)和式(7)代入式(3)和(4)即可得到AWGN信道下“与”规则协作检测的虚警概率和检测概率。
平均感知比特数公式中只有Λ1受信道衰落影响,所以AWGN信道下通过“与”规则对上报信息进行融合的归一化平均感知比特数将式(1)中的Λ1替换为=ΨAWGN(λ1)-ΨAWGN(λ0)即可。
2.1.2 Nakagami信道下“与”融合
在无线移动通信环境中,针对多径效应影响引起的快衰落,Nakagami分布能较好地逼近实际信道。
如果认知用户和融合中心之间的信道是Nakagami信道,H1假设下能量E的累积函数为:

式中,1F1(.;.;.)为 Confluent Hypergeometric 函数[8]文献[2]对文献[1]中A1表达式进行了修正。
如同式(6)和式(7)可以得到Nakagami信道下的Pα和Pβ。将其代入式(3)和式(4)即可得到Nakagami信道下“与”规则协作检测的虚警概率和检测概率。
Nakagami信道下通过“与”规则对上报信息进行融合的归一化平均感知比特数将式(1)中的Λ1替换为
2.2 Nakagami信道下基于簇的融合
基于簇理论的协作感知方法能有效减小衰落传送信道上的传输错误影响,从而使协作感知性能得到提高。这里选用利用选择分集的合作检测方法,首先设置以下2个假设:
①在协作感知系统中,对于所有认知用户传送信道的瞬时信道状态信息都是可知的;
②在同一个簇中,每两个认知用户中间的信道为Nakagami信道。
基于簇理论的协作感知方法原理如图1所示。
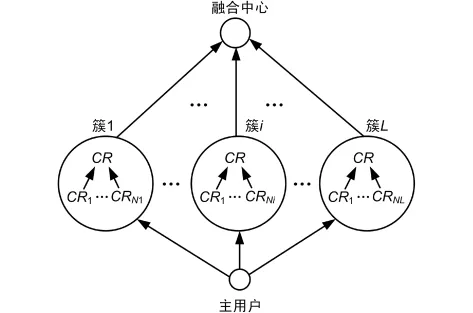
图1 基于簇理论的协作感知方法原理
首先将所有认知用户(即图中的CR)分成L个簇(Ni为每簇所拥有的认知用户个数),然后,在簇中选择报告信道瞬时SNR最大的认知用户作为簇首。通过如下步骤完成协作感知:第1步,所有认知用户进行本地感知,并将本地决策上报给簇首;第2步,每个簇首使用“与”融合规则对簇中别的认知用户上报的信息进行汇总,并将决策信息上报给融合中心;第3步,融合中心使用“与”规则得出最终决策。
基于簇理论的协作感知策略的归一化平均感知比特数[7]为:

由于每簇间即每簇认知用户和簇首之间的信道都是独立同分布的,所以 Ω(λi)=Ω(λ),。
对于第i个簇,在H0与H1下不作判决的概率分别为Λ0i=Ω(λ1i)-Ω(λ0i),Λ1i=Ψ(λ1i)-Ψ(λ0i);失败感知概率分别为δ0i=与δ1i=。
如果认知用户和簇首之间的信道是Nakagami信道,如同式(6)和式(7)可以得到第i个簇的Pα和Pβ,将其代入式(3)和式(4),可得各簇的虚警概率和检测概率。
融合中心使用“与”规则对各簇首上报的信息进行融合,所以最终融合后得到的虚警概率和检测概率为:
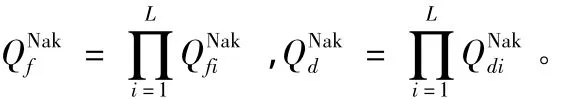
3 仿真结果分析
这里对衰落信道下“与”规则融合与基于簇的协作感知方案下检测概率和归一化平均感知比特数进行了仿真。选取仿真参数如下:P0=0.5,u=5,Nakagami参数m=2,认知用户与主用户之间的信道平均信噪比SNR=10dB,H0假设下的失败感知概率 δ0=0.001 。
图2比较了“与”准则融合与基于簇的协作感知方案下的检测概率,选用AWGN和Nakagami两种衰落信道,设定协作感知网络中共有10个认知用户。从图中可以看出AWGN信道下将网络中的10个认知用户分为2簇,每簇5个认知用户进行协作感知得到的检测概率要明显优于10个认知用户通过“与”规则融合后得到的检测概率。在Nakagami信道下进一步证明了基于簇理论的协作感知性能好于“与”融合的协作感知性能。
从图3可以看出,在AWGN和Nakagami信道下基于簇的协作感知平均感知比特数要多于通过“与”融合的协作感知,即基于簇理论的协作感知方案在获得较高的检测概率的同时要消耗更多的感知比特数。

图2 “与”规则与基于簇的融合方案的检测概率比较
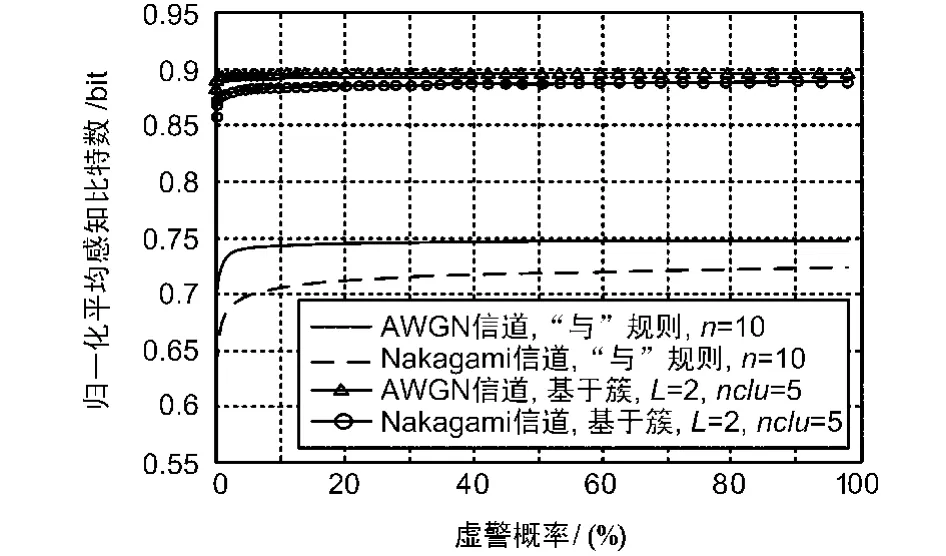
图3“与”规则与基于簇的融合方案的感知比特数比较
下面分析不同的分簇方法对感知性能和归一化平均感知比特数的影响,这里选用模拟实际通信环境的Nakagami信道,设定协作感知网络中认知用户个数为12。分析图4和图5得到,当协作感知网络中认知用户数一定时,分成的簇数越多,每簇中认知用户数越少,检测概率越大,但是消耗的感知比特数也越多。

图4 Nakagami信道下检测概率的比较

图5 Nakagami信道下归一化平均感知比特数的比较
4 结束语
上述对衰落信道下“与”规则融合协作感知的性能进行了分析,提出了基于簇理论的协作感知方法,通过仿真分析得出,基于簇的协作感知相比于“与”融合协作感知虽然会消耗更多的感知比特数,但是能获得更高的检测概率。
[1]D IGHAM F F,ALOUNI M S,SIMON M K.On the Energy Detection of Unknown Signals over Fading Channels[J].IEEE.Trans.Commun.,2007,55(1):21 -24.
[2]L IU Yun-xue,YUAN Dong-feng,JIANG Ming-yan,et al.Analysis of Square-Law Combining for Cognitive Radios over Nakagami Channels[C].WiCom'09 5th International Conference on,2009:1 -4.
[3]W U Jin-bo,LUO Tao,YUE Guang-xin.An Energy Detection Algorithm Based on Double Threshold in Cognitive Radio Systems[C].IEEE.Trans.The 1st International Conference on Information Science and Engineering,2009:493-496.
[4]S UN Chun-hua,ZHANG Wei,LETAIEF K B.Cooperative Spectrum Sensing for Cognitive Radios under Bandwidth Constraints[C].Wireless Communications and Networking Conference,IEEE,2007:1 -5.
[5]卞 荔 ,朱 琦.基于表决融合的带宽受限的协作频谱感知算法[J].信号处理,2010(8):1 143-1 150.
[6]S UN Chun-hua,ZHANG Wei,BEN K.Cluster-based Cooperative Spectrum Sensing in Cognitive Radio Systems[C].Communications,IEEE International Conference on,2007:2 511-2 515.
[7]B AI Zhi-quan,WANG Li,ZHANG Hai-xia,et al.Clusterbased Cooperative Spectrum Sensing for Cognitive Radio under Bandwidth Constraints[C].Communication Systems(ICCS),IEEE International Conference on,2010:569 -573.
[8]G RADSHTEYN I S,RYZHIK I M.Table of Integrals,Series,and Products,Seventh ed [M].San Diego,CA:Academic Press,2007.

