基于有限容积的电缆群载流量计算和分析

于建立，隋琳琳，田际平，李艳飞，胡国伟

(1.东北电力大学输变电技术学院，吉林吉林132012;2.东北电力大学电气工程学院，吉林吉林132012;3.吉林省电力有限公司超高压公司，长春130000)

随着电力电缆在电网建设中应用的越来越广泛，电缆各种物性参数的准确获取以及对载流量的精确计算，对电缆应用的经济性和安全性意义越来越大。目前国内众多的电缆载流量计算标准是按照国际电工委员会推荐的IEC60287方法［1］。该方法基于电缆热流场的原理以电缆等值热路［2］为基础，通过计算电缆热源和各部分热阻并结合其最高工作温度限制，给出了敷设于均匀土壤中电缆载流量解析计算方法。对敷设于不均匀土壤中电缆载流量的计算，IEC标准给出了通过校正系数计算电缆外部热阻的修正方法，可以计算敷设于几何形状规则的回填土中电缆的载流量。校正系数的引入会影响计算的准确性，计算表明该误差会随着回填土热阻系数的增大和电缆数增多而增大。校正系数的选取是一个十分复杂的问题，工程中缺乏可靠的校正依据。靠试验获取校正系数工作量太大且成本太高，而数值计算方法具有成本低及能模拟任意复杂工况等优点，比IEC计算方法准确，可以拓宽试验研究范围。数值计算的计算速度较解析方法耗时长，电缆回路越多该局限性越明显。为此，本文以有限容积法为基础，将数值方法得到的土壤温度场与电缆等值热路法相结合求解缆芯温度和载流量，同时具备数值计算的高精度和解析计算的高效率。

1 公式法计算电缆载流量

式中，I为一根导体中流过的电流，A;Δθ为电缆缆芯与周围媒质的温差，℃;Wd为绝缘层单位长度损耗，K/m;T1、T2、T3、T4分别表示绝缘层、内衬层(或阻水层)、外护套和周围媒质的热阻，K·m/W;R为电缆缆芯在最高温度时导体单位长度的交流电阻，Ω;n为每根电缆的线芯个数;λ1、λ2分别为电缆金属护套

ee为电缆外径，m;d1K，d2K……dNK分别为电缆1，2，……N的中心至K电缆中心的距离，m;d'1K，d'2K……d'NK分别为电缆1，2，……N的镜像中心至K电缆中心的距离，m。对不均匀土壤中电缆外部热阻T'4，IEC标准在T4基础上加入修正项进行修正计算。

2 数值计算方法

2.1 物理模型和数学模型

根据电缆发热的物理特点，将该模型看作是具有内热源的闭域导热问题。电缆的长度远远大于电缆的半径，长度方向温度几乎不变化，故可将该模型简化为二维。数值计算采用通用的导热微分方程为［3］:

取垂直于x-y平面方向上的厚度为1，(ΔxΔy)即为控制容积的体积(如图1)。在无热源区内，热源项Q值取为0。

2.2 边界条件处理

计算传热学问题的边界条件可归纳为三类［4-5］:第一类为边界温度已知，即为恒温边界，第二类边界条件为已知边界法向热流密度，第三类边界条件为已知界面上的对流换热系数以及流体温度，坐标组合法的边界条件分为以下三部分:

(1)距电缆足够远的两侧和底部取第一类边界条件，一般为当地土壤温度的平均值;(2)与空气层接触的上边界以牛顿冷却公式考虑对流散热［6］，控制方程为:

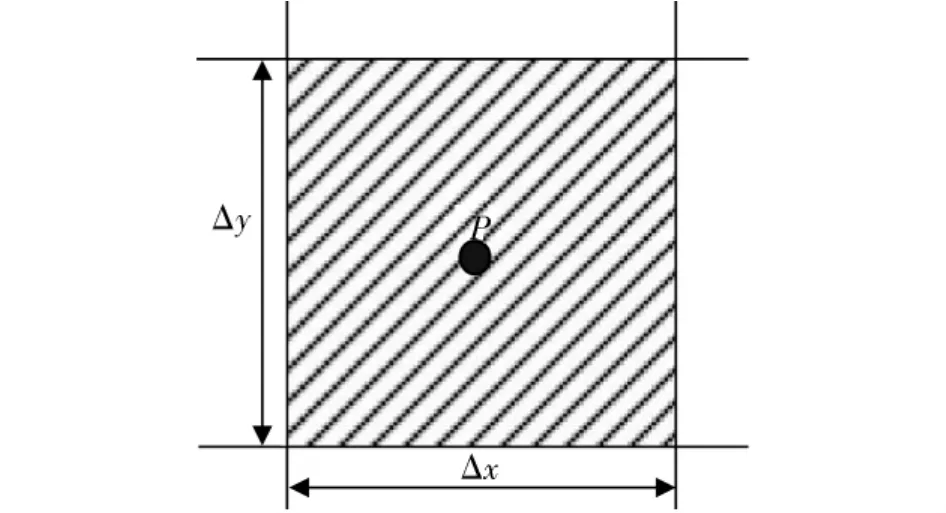
图1 温度场内的控制容积

式中:λT为地表土壤导热系数，W/(m·K);TT为地表面土壤层温度，℃;TA为地表面空气温度，℃;h为地表面的冷却散热系数，W/(m2·K)。

(3)在电缆各层以及电缆和周围媒质之间的分界面上，采用热流连续性定理来处理:

式中:λ1，λ2分别为介质1和介质2的导热系数W/(m·K)，l为垂直于介质1和介质2之间分解面的法线。

2.3 计算方法

本文在文献［7］的基础上提出了一种计算电缆温度场与载流量的新方法。该方法采用有限容积法计算电缆周围温度场，并采用等值热路法计算缆芯温度，既能保证计算的准确度又非常有效地加快了计算速度。将包括电缆在内的导热区域进行不均匀(电缆区域密集，远离电缆区域稀疏)直角网格划分，电缆本体划分到相应的直角网格内，任一网格内导热参数的赋值根据其介质来确定。绝缘和金属护层损耗远小于缆芯损耗，可将前二者的损耗等效到缆芯损耗中，将缆芯所在的直角网格被作为热源处理。电缆的各层厚度不等，为减少网格划分带来的误差并提高计算效率，采用调和平均法计算除缆芯导体外的电缆层等效导热系数［5］。直角坐标温度场收敛后结合直埋电缆热平衡方程［2］可得缆芯温度值:

图2 电缆外围土壤温度

3 数值计算验证及计算分析

3.1 数值计算的试验验证

笔者采用基于场路结合的有限容积法编程，并同试验结果进行了比较。如图3所示，试验中将电缆简化为只有导体和外护套两层结构。用土壤直埋带绝缘的发热管加热试验验证仿真计算程序在电缆温度场计算中的有效性。试验的土壤导热系数为1.664 W/(m·K)，空气和土壤的对流换热系数为12.5 W/(m2·K)，埋深 0.5 m，发热管半径为0.006 m，长度为2.5 m，发热管的电阻120 Ω，地表空气温度30℃，土壤深层温度25℃，绝缘层导热系数为0.25 W/(m·K)，绝缘层厚度0.004 m，发热棒两端电压为120 V。该试验在温度场达到稳态值时，导体温度的测量结果为53℃，本文程序的计算结果为54.3℃，以试验为基准，本文计算误差为1.3℃。说明本文的计算方法具有较高的计算精度。

图3 试验模型示意图

3.2 数值计算分析

3.2.1 电缆纵向排列的载流量和IEC计算方法的误差

电缆集群纵向排列(如图4)，在土壤热阻系数为1.0 K·m/W的均匀土壤中表1给出了本文数值方法和IEC修正方法计算出110 kV630 mm2铜芯XLPE绝缘电缆的载流量随回路数的变化。Ie为IEC方法计算的载流量，Ib为本文数值计算方法计算的载流量。由表1可见:由于电缆间存在互热效应，电缆集群载流量随回路数的增加而显著减小，七回路电缆集群的载流量仅为单回路电缆载流量的50%。均匀土壤中IEC计算电缆集群的载流量具有较高的精度，以数值计算结果为准，其最大误差不超过3.4%。

图4 电缆纵向敷设示意图

3.2.2 回填土热阻系数对电缆集群载流量的影响以及IEC误差的影响

表1 均匀土壤电缆集群的载流量与IEC的误差

图5和图6分别给出了两回路和六回路布置时，本文数值和IEC方法计算的110 kV630 mm2铜芯XLPE绝缘电缆集群载流量随回填土热阻系数的变化。由图5和图6可见，电缆纵向排列IEC算法对两回路载流量计算具有较高的计算精度，而对于六回路电缆载流量则在回填土热阻系数较大时，出现明显的计算误差。例如回填土热阻系数为周围土壤热阻系数的2.5倍时，IEC计算误差达到-10.1%。

图5 两回路载流量计算结果比较

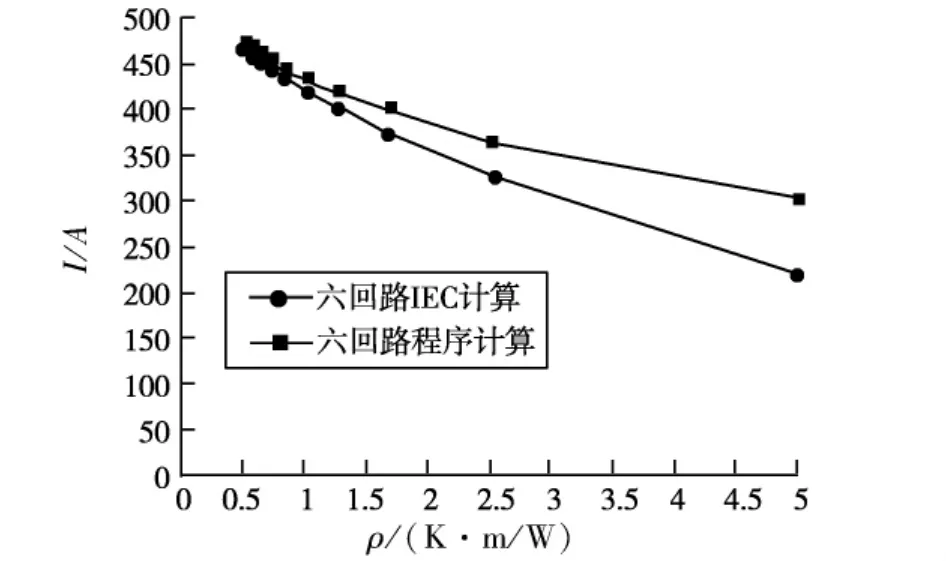
图6 六回路载流量计算结果比较

4 IEC计算误差原因分析

IEC计算方法的精度取决于外部热阻的计算精度。图7和图8分别给出了纵向两回路和六回路IEC公式计算的外部热阻和本文数值计算方法反推得出的外部热阻。由图7可见，纵向两回路敷设时，IEC公式计算外部热阻精度较高，故载流量计算精度高;由图8可见，纵向六回路敷设时，IEC公式计算回填土热阻系数较小时，与数值计算方法吻合，而在回填土热阻系数较大时，IEC公式计算的外部热阻明显偏大，所以其载流量计算结果偏低。

图7 纵向两回路外部热阻计算结果比较

图8 纵向六回路外部热阻计算结果比较

5 结 论

本文计算电缆温度场的场路结合方法是基于坐标组合的基础，实现了数值计算和解析计算的有效结合。既具有较高的准确性和实用性，又可提高计算效率，尤其对电缆集群的计算。对有回填土的不均匀土壤中电缆集群载流量计算，IEC标准的修正方法有一定误差，该误差在回填土热阻大时会增大，导致电缆回路越多计算精度越低。本文的数值计算方法可有效解决该问题。

［1］International Electrotechnical Commission.IEC 60287 -1.Calculation of current rating part 1:(100%load factor)and calculation of losses［S］.2001.

［2］郑肇骥，王明.高压电缆线路［M］.北京:水利水电出版社，1983.

［3］陶文铨.数值传热学［M］.西安:西安交通大学出版社，2001.

［4］杨世铭，陶文铨.传热学［M］.北京:高等教育出版社，1998.

［5］梁永春，李彦明，柴进爱，等.地下电缆群稳态温度场和载流量计算新方法［J］.电工技术学报，2007，22(8):185-190.

［6］詹士昌.牛顿冷却定律适用范围的探讨［J］.大学物理，2000，19(5):36-37.

［7］曹惠玲，王增强，李雯靖，等.坐标组合法对直埋电缆与土壤界面温度场的数值计算［J］.电工技术学报，2003，18(3):59-63.