一种基于飞行平台的数字稳像及目标跟踪系统
刘承平,袁 飞
(1.中国电子科学研究院,北京 100041;2.中国科学院自动化研究所,北京 100190)
0 引 言
飞行器稳像及运动目标跟踪技术是空基或天基视频监控系统的一项关键技术。它们在可视预警、无人驾驶飞机、机器人导航、光电成像制导及目标跟踪等军用和民用领域有着广泛的应用,也发挥着重要的作用。
由于飞行平台可能存在振动、旋转和姿态变化,成像装置输出的图像可能会产生严重的平移、旋转和伸缩变化。例如,安装在旋转弹体的光电成像导引头,弹体在经过解旋后,其飞行末段的弹体旋转速度仍可能达到5 ~20 转/秒。在未采用稳像措施下,光电成像导引头输出的图像一般都会出现严重的像旋和图像模糊,致使其无法正常工作。数字稳像技术能够估计、补偿图像序列帧间的运动,从而消除成像传感器平台(如飞行平台)的运动带来的影响。不同于光学稳像技术,数字稳像技术不依赖于陀螺、定位传感器和光学仪器等专用硬件,适合于那些对体积、重量和功耗要求极其苛刻的飞行平台使用,因此得到了广泛的应用[1~4]。
尽管许多文献致力于解决数字稳像问题,真实场景中抖动图像序列的稳像问题仍然是一个极具挑战性的难题。这些难题主要体现在如下几个方面。(1)真实场景中运动的复杂性:不仅包括平移运动,还包括缩放,旋转,斜切等运动;(2)大的旋转运动:相对于大的平移运动来说,大的旋转运动更加难以解决;(3)前景目标的影响;(4)背景的复杂性,背景往往是不断发生变化的;(5)系统的实时性要求。
针对帧间的平移运动及包括适当旋转(<15°)在内的稍复杂的运动,一些学者提出了一些有效的数字稳像算法[3,5~8]。文献[5]提出了一种基于特征的快速视频稳像算法。该算法通过跟踪少量的特征集合估计出帧间摄像机的运动。但是该算法仅能估计出帧间的平移运动和小范围的旋转运动(<10°)。一些学者提出在频域中估计帧间的运动参数[6,7]。这些算法利用空域中的像移对应于频域中的相位移动这一属性估计出帧间的平移运动。文献[8]对基于频域的方法进行了改进,其通过引入极坐标来解决旋转运动和缩放运动。基于频域的方法仅仅能够估计出帧间全局的旋转、缩放和平移运动,当场景由多个独立运动的目标组成时,算法往往不能输出精确的运动参数。
本文的目标在于稳定帧间存在任意角度的旋转运动,较大的缩放运动和平移运动的图像序列。为了对任意角度的旋转,较大的缩放和平移运动进行估计,提出了一种基于log-polar 变换的数字稳像算法。算法由运动估计单元和运动修正单元两部分组成。在运动估计阶段,提出了一种多分辨率log-polar 变换技术估计出任意角度的旋转,较大的缩放和平移运动。运动修正单元由运动补偿模块和图像合成模块构成,用来补偿当前帧图像的运动,以生成稳定的图像序列。
在解决了飞行平台成像装置的稳像问题之后,构建了一个基于飞行平台的运动目标跟踪系统。在此系统中,采用了基于ICA 的运动目标跟踪算法[9]对图像序列中指定的运动目标进行跟踪。与经典的Lucas-Kanade 跟踪算法[10]相比,ICA 跟踪算法转换了模板图像与输入图像的关系,运行预先计算雅可比矩阵和海森矩阵,在保证跟踪精度的同时,极大地提高了计算效率。

图1 本文的算法流程图
以下章节安排如下:第1 部分详细介绍基于log-polar 变换的数字稳像算法;第2 部分介绍基于ICA 的运动目标跟踪技术;最后,在第3 部分对提出的方法进行了实验验证。
1 基于log-polar 变换的数字稳像算法
1.1 Log-polar 变换(LPT)技术
假设I(x,y)是笛卡尔坐标系下的图像,I*(r,θ)是对数极坐标系下变换后的图像,(x0,y0)是变换中心。对数极坐标变换可表示为
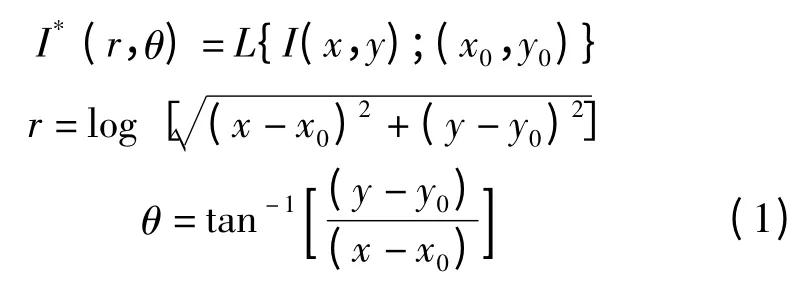
对数极坐标变换的优点在于其能将笛卡尔坐标系下图像的旋转和缩放变化变换为对数极坐标系下θ 轴和r 轴的平移运动。因此,原始图像I(x,y)中的旋转对应于I*(r,θ)中θ 轴上的平移,图像I(x,y)中的缩放对应于I*(r,θ)中r 轴上的平移。假设是I1和I2两幅原始图像,和分别是I1和I2对应的经过log-polar 变换后的图像。如果I2是I1经过旋转和缩放后的变换图像,那么,将是在θ 轴和r 轴方向上的平移图像。一个典型的示例如图2 所示。图2(a)是原图像,图2(b)是原图像在笛卡尔坐标系下变换后的图像,其中,缩放倍数为2,旋转角度为90°。它们经过log-polar 变换后的图像分别为图2(c)和图2(d)。通过比较图2(c)和图2(d),可以看出:图2(d)是图2(c)在水平轴方向上移动了128列(整幅图像为512 列),对应了图2(a)的90°旋转;图2(d)是图2(c)在垂直轴方向上移动了32列,对应于图2(a)的2 倍的放大。

图2 Log-polar 变换示例
1.2 基于多分辨率log-polar 变换的运动估计
利用log-polar 变换,成功地在试验图像上估计出任意大小的旋转运动和0.5 ~4 倍的缩放变化。但是,使用log-polar 变换技术进行运动估计需要知道两幅图像对应变换原点的位置。在上述示例中,假设两幅图像的原点位于它们的几何中心。实际中,它们的原点可能会产生偏移,而且这种偏移量是未知的。
为了估计出两幅图像的对应变换原点,我们提出了一种由粗到细的多分辨率的搜索策略:首先,在第一幅图像的几何中心处取一个具有一定大小圆周模版,并进行对数极坐标变换;然后,对第二幅图像搜索区域的每一个位置,以它们为圆心选取同样大小的圆周区域,进行log-polar 变换,并且将其与参考模板图像变换后的图像进行交叉相关运算,此时可以得到一个最优相关值和对应的旋转、缩放参数;最后,比较搜索区域中所有位置最优相关值的大小,把最大值点处的旋转和缩放参数,以及此点相对于图像中心的平移量作为最优的旋转,缩放和平移参数。
试验中,在3.06 GHz Pentium 4 PC 机上对2 幅640 ×480 的图像进行运动估计,采用3 级金字塔逐级进行运动估计,圆周半径为40 个像素,搜索区域为160 ×120 个像素,用了3 s 的时间。这样的速度限制了此算法的实际应用。上述算法之所以计算量大,是由于搜索区域的每一个像素都要进行log-polar变换和交叉相关匹配运算。尽管采用了由粗到细的3 级金字塔技术简化了运算,但是在最低级的金字塔图像上仍然有许多像素点需要进行变换和匹配。
1.3 基于旋转不变特征的快速搜索算法
如果能首先大致确定输入图像中对应原点的位置,计算量将会大大减少。根据这个思想,提出了一种基于旋转不变特征的快速搜索算法。这种快速搜索算法能大致确定输入图像中对应原点的位置,使得搜索窗口的滑行窗口限定在有限区域内,而原点不可能存在的区域则不进行计算,因而大大提高了搜索效率。
基于旋转不变特征的快速搜索算法包括如下两个模块:特征生成模块和圆周块匹配模块。
1.3.1 特征生成
为了保证足够的匹配精度及相对低的匹配复杂度,根据试验结果选取了4 种有效的特征。这4 种特征从模板图像的两个特征图像中提取:亮度图像I 和梯度图像G。为了保证所提取特征的旋转不变性,梯度算子应该具有旋转不变性。因此,采用高斯拉普拉斯算子(LoG)生产梯度图像,因为高斯拉普拉斯算子[11]具有旋转不变性,并且高斯滤波器[12]具有圆周对称性。实际中,只有强的边缘对于块匹配才是值得信赖的,引入了如下阶梯函数以去除梯度图像G 中的弱边缘
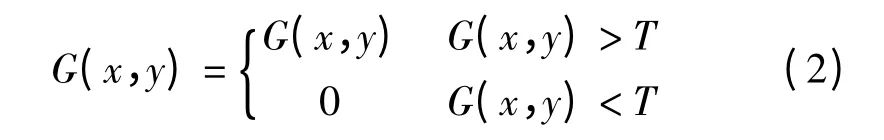
式中,T 是一个阈值,经验地设置为20。
4 种特征g1,g2,g3,g4可由下式从圆周块区域中提取
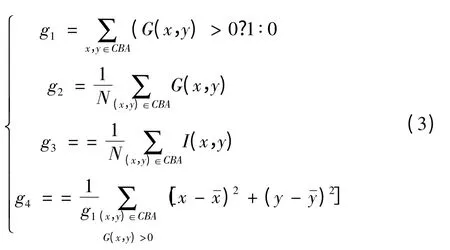
1.3.2 圆周块匹配
圆周块匹配是一种二维的运动搜索过程,其目的在于在输入图像中寻找模板圆周块的最佳匹配位置。假设圆周块A 是模板图像中指定的模板圆周块,A′是输入图像中与圆周块A 具有相同中心坐标的圆周块,C′是搜索区域中的参考块。使用特征向量的一维正则化差分向量作为匹配准则,可以求出最佳匹配块A′
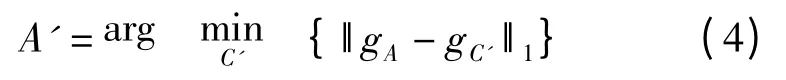
模板图像与输入图像对应原点的偏移量可由A和A′的运动偏移向量(dxA-dxA′,dyA-dyA′)确定。
2 基于Inverse Compositional 算法的运动目标跟踪算法
在解决了高速旋转的飞行平台的稳像之后,提出了一种基于ICA[9]的运动目标跟踪算法。该方法通过对所选择目标与输入图像的对准实现对目标的跟踪。其基本思想是:建立描述指定目标区域形变和运动的参数运动模型,然后把目标跟踪问题转化为求取上述运动模型的参数最优化估计问题。传统的基于对准的跟踪算法,比如Lucas-Kanade 算法[10],在每次迭代中都要计算雅克比矩阵和海森矩阵,效率低下,难以达到实时性的要求。ICA 算法是对Lucas-Kanade(L-K)算法的改进,其转换输入图像与模板的关系,允许预先计算耗时的雅克比矩阵和海森矩阵,具有非常高的计算效率。同时,ICA 算法是一种基于梯度下降的最优化算法,具有较高的参数估计精度。本章利用了ICA 算法在计算方面的简洁性和精度高的特点,使用其对目标进行精确地跟踪。
Lucas-Kanade(L-K)算法的目标在于最小化模板图像T(x)与输入图像I(x)的平方误差和
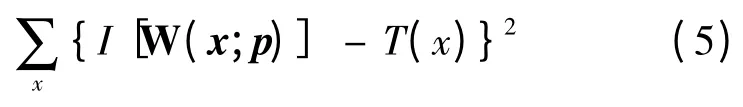
式中,x=(x,y)T表示像素坐标的列向量;W(x;p)是运动模型的参数集合,其将模板图像T(x)的像素x 的坐标映射到输入图像I(x)的子像素位置,p =(p1,p2,…,pn)T。对于2D 平面上运动的近似平面图像块,W(x;p)可以表示为
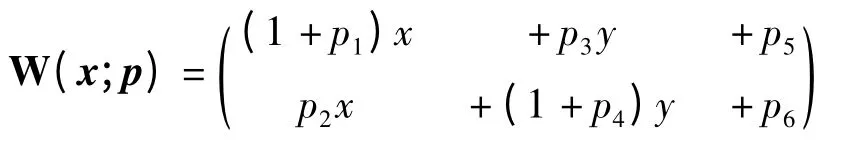
ICA 算法转换了模板图像T(x)与输入图像I(x),即最小化
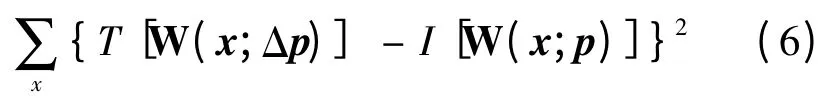
对于非线性表达式(6),可由以下更新迭代求出运动参数
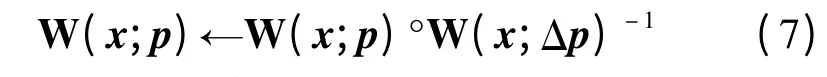
式中,W(x;Δp)-1是W(x;Δp)的逆运算。当||Δp||≤ε 时,迭代停止(其中,ε 是迭代停止阈值)。详细推导可参考文献[9]。
通过计算移动目标在图像序列中相邻帧间的运动模型参数Wt(x;p),可以估计出运动目标的运动,从而实现对指定运动目标跟踪。
3 实 验
在某飞行器光电成像器输出的真实数据集上进行了实验。
首先,采用如下指标对文中提出的稳像算法进行了实验:准确度(Fidelity)、位移范围(Displacement Range)和性能(Performance)。
准确度是指衡量稳像算法补偿摄像机运动好坏的一个评价标准,比如,运动模型对摄像机运动的估计精度。准确度常常使用峰值信噪比(PSNR)作为品质因子,其定义如下
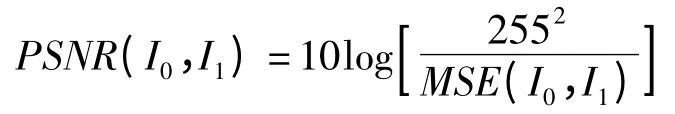
式中,MSE 是两幅图像像素值的均方误差值,它反应了两幅图的差异大小。PSNR 越高,两幅图像的内容差异越小,当它们完全重合时,PSNR 达到最大。
真实图像序列稳像结果的PSNR 值比较如图3所示。图3 中位于顶端的曲线代表稳像后的图像与参考图像之间的PSNR 值,下端的折线代表输入图像与参考图像之间的PSNR 值。从图3 中可以看出,文章提出的稳像算法显著地提高了输入图像与参考图像之间的PSNR 值。
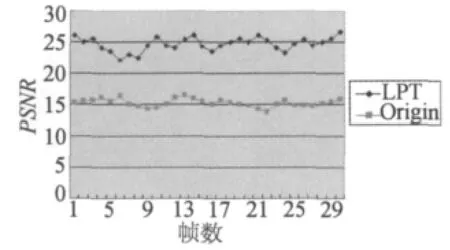
图3 真实场景图像序列的稳像结果的PSNR 比较
位移范围指稳像系统能够实现的运动估计的最小分辨率和最大稳像范围。最小分辨率是指稳像算法中运动估计算法的精度。最大稳像范围是评价稳像系统性能的另一个重要指标。通常来说,对选取的运动估计算法,在保持稳像精度的情况下,可估计的图像的最大偏移量越大,系统可矫正的图像的偏移量也越大。

表1 LPT 稳像算法的位移范围
性能是指稳像系统能够补偿的最大位移速度,通常定义为帧率与最大帧间平移量的乘积。帧率是稳像系统的一个重要评价指标,但是仅仅使用帧率衡量稳像系统的性能是不合适的。因为可以通过牺牲系统的鲁棒性和精度及运动估计的范围来提高系统的帧率。在实验中,使用旋转速度作为性能指标。在3.06 GHz Pentium 4 的PC 机上进行了实验,当搜索窗口大小为160 ×120 时,LPT 稳像算法的帧率为4.5 帧/秒。因此,LPT 稳像算法的最大旋转速度为:4.5 ×360 =1620。
下面,对文中提出的基于飞行器平台的运动目标跟踪系统的综合性能进行测试。该系统首先对飞行器光电成像器输出的帧间存在较大旋转的抖动图像序列进行稳像,然后在稳定的图像序列中对场景中的指定目标进行跟踪。基于真实图像序列的试验结果如图4 所示。

图4 真实场景图像序列的稳像和跟踪示例
试验结果表明,该系统能够实现对抖动图像序列的稳像和对指定目标的跟踪。而在未采取稳像措施之前,是不可能对图中的指定车辆进行跟踪的。
4 结 语
首先提出的基于log-polar 变换的数字稳像算法,具有以下优点:(1)能够对存在任意大小的旋转,较大的缩放(0.5 ~2 倍)和平移运动(±80 个像素)的图像序列进行稳像,并且可以推广解决更复杂的运动情形下的稳像,如仿射运动,透视投影运动等;(2)稳像精度高;(3)算法适应性强,不依赖典型的特征,不需要任何先验知识。
还提出了一种基于ICA 的运动目标跟踪算法,并将上述稳像算法融合在一起,组成了一个基于飞行器平台的运动目标跟踪系统。基于真实的图像序列的试验结果表明,该系统能够实现对抖动图像序列的稳像和对指定目标的跟踪。
[1] BURT P,ANANDAN P. Image Stabilization by Registration to a Reference Mosaic[C]//DARPA Image Understanding Workshop,In Proc:Monterey,CA,1994:425-434.
[2]MORIMOTO C,DEMENTHON D,DAVIS L,et al.Detection of Independently Moving Objects in Passive Video[C]//Of Intelligent Vehicles Workshop,In Proc:Detroit,MI,1995:270-275.
[3]刘栋,赵跃进,尹德森,等. 基于特征点跟踪的数字稳像算法[J]. 光学技术,2008:281-284.
[4]仲训昱,朱齐丹,张智.数字稳像中的快速和鲁棒运动估计研究[J]. 电子学报,2010:251-256.
[5]MOHAMMED A ALHARBI,et al. Fast Video Stabilization Algorithms[D].AIR FORCE INSTITUTE OF TECHNOLOGY,AFIT/GCS/ENG/06-02.
[6]KIM S,SU W. Subpixel Accuracy Image Registration by Spectrum Cancellation[C]//IEEE International Conference on Acoustics,in Proc:Speech and Signal Processing,1993:153.
[7]STONE H,ORCHARD M,CHANG E,et al. A Fast Direct Fourier-Based Algorithm for Subpixel Registration of Images[J]. IEEE Transactions on Geoscience and Remote Sensing 39,2001:2235-2243.
[8] MARCEL B,BRIOT M,MURRIETA R. Estimation of Translation and Rotation by Fourier Transform[C]//Traitement du Signal,1997,14:135-149.
[9] SIMON BAKER,IAIN MATTHEWS. Lucas-Kanade 20 Years on:A Unifying Framework[J]. International Journal of Computer Vision,2004,56(3):221-255.
[10]LUCAS B,KANADE T. An Iterative Image Registration Technique with an Application to Stereo Vision[J]. The International Joint Conference on Artificial Intelligence,1981:674-679.
[11] MORIMOTO C,CHELLAPPA R. Fast Electronic Digital Image Stabilization[C]//IEEE Proc.of International Conference on Pattern Recognition,1996,3:284-288.
[12] SONKA M,HLAVAC V,BOYLE R. Image Processing,Analysis,and Machine Vision[M]. ISBN:049508252X,Plenum Press:Chapman/Hall,1993:81-88.

