非弹性结构体系的概率地震损伤分析
余 波,杨绿峰,2
(1.广西大学 工程防灾与结构安全教育部重点实验室,南宁530004;2.广西壮族自治区 住房和城乡建设厅,南宁530028)
地震动对工程结构的作用实际上是一个能量的输入、转化与耗散的过程。结构在地震作用下不仅会产生变形,而且会发生能量耗散,两者都会对结构造成不同程度的损伤。因此,地震作用下结构的最大位移响应和能量耗散能力是结构抗震设计的2个重要性能指标[1]。
由Park等[2-3]提出的地震损伤指标综合考虑了结构的最大非弹性位移和累积滞回耗能的影响,是目前比较常用的地震损伤模型。杨伟等[1]根据能量方程建立结构最大弹塑性位移和累积滞回耗能的关系,提出了Park-Ang地震损伤指标的简便算法。王东升等[4]根据钢筋混凝土构件低周疲劳试验数据,利用临界延性系数和能量等效系数来确定能量项加权因子,提出了改进的Park-Ang地震损伤模型。于琦等[5]通过建立多自由度体系与等效单自由度体系之间滞回耗能的转化关系,提出了基于变形与能量双重准则的钢筋混凝土结构地震损伤评估方法。易伟建等[6]利用Pushover建立多自由度体系结构与等效单自由度体系之间位移及能量的转换关系,进而采用Park-Ang模型对结构的整体地震损伤程度进行了综合评估。Ghosh等[7]比较了确定平面多层框架Park-Ang地震损伤指标的三种等效单自由度体系方法。张国军等[8]分析了加载循环水平对高强混凝土框架柱累积滞回耗能的影响规律,进而确定了适用于高强混凝土框架柱的Park-Ang损伤模型的耗能因子。傅剑平等[9]根据钢筋混凝土柱的试验数据,对钢筋混凝土结构的Park-Ang双参数破坏准则的识别和修正问题进行了讨论。
值得注意的是,现有的研究主要针对单向地震激励下的理想弹塑性或双线性结构体系进行分析,而对于双向地震激励下具有强度退化、刚度退化、捏拢效应等典型滞回特性的结构体系的地震损伤关注较少。然而,实际工程结构大多承受双向地震激励,特殊情况下还有必要考虑竖向地震作用和转角激励的影响[5]。此外,震害资料和试验数据显示,钢筋混凝土结构在地震作用下往往发生混凝土开裂、破碎、剥落甚至压溃,钢筋与混凝土之间也会发生粘结滑移,结构整体表现出明显的强度退化、刚度退化、捏拢效应等典型滞回特性。鉴于此,笔者引入规一化屈服强度和规一化位移的概念,并利用规一化位移作为控制参数,以圆形屈服面来描述双向规一化恢复力之间的耦合效应,且综合考虑强度退化、刚度退化、捏拢效应等典型滞回特性的影响,建立了双向地震激励下非弹性双自由度体系地震损伤分析的新型数值模型,并结合所筛选的69条地震记录定量地分析了非弹性2DOF体系的地震损伤指标的概率统计特征。
1 地震延性需求和损伤指标
如图1所示,双向水平地震激励下非弹性双自由度体系的运动控制方程为式(1)。

式中:m为集中质量;下标i(i=x和y)表示地震激励和结构响应的方向;ki和c i分别表示初始线弹性刚度和粘滞阻尼系数;αi为屈服后刚度比;和为地震加速度;ubi、bi和bi分别表示集中质量的相对侧向位移、速度和加速度;zbi为非线性滞回位移。
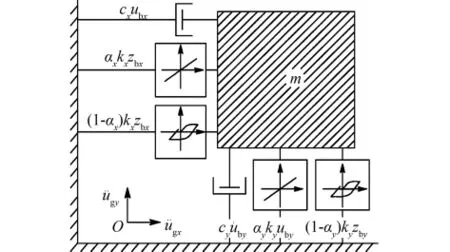
图1 双向地震激励下的非弹性2DOF体系
假设在单向水平地震激励下,线弹性体系的位移峰值为Dei(i=x,y),非弹性体系在屈服点处的位移为Dyi,则可以引入无量纲量[10],得到式(2)、(3)。
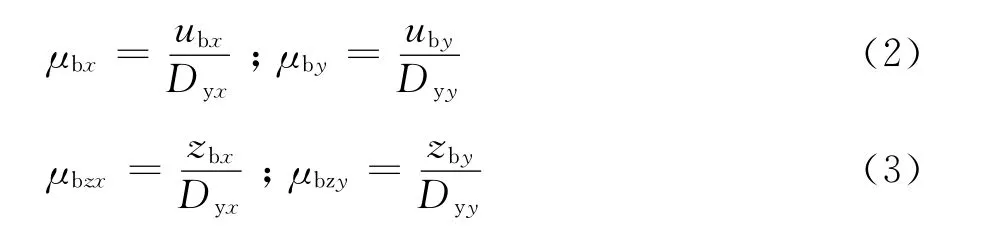
式中Dyi=φi Dei;φi为规一化屈服强度;μbi和μbzi分别表示集中质量在双向地震激励下的规一化侧向位移和规一化滞回位移。利用式(2)所定义的无量纲量,可以将式(1)表示为式(4)。
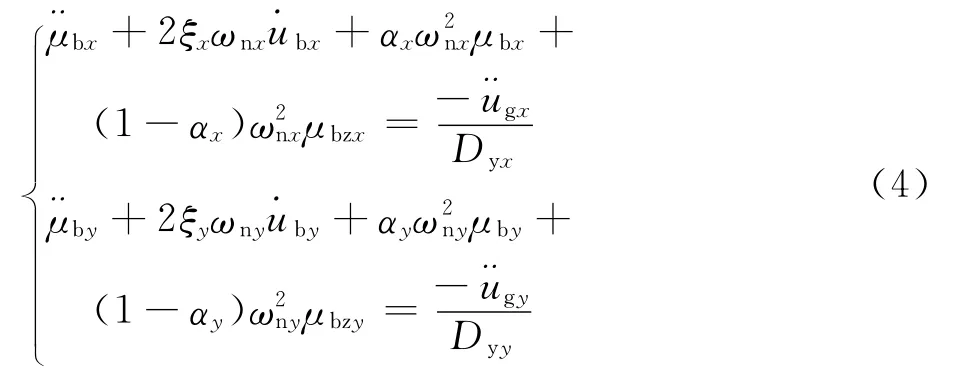
式中ξi=ci/(2mωni)和ωni= (ki/m)0.5分别表示非弹性体系在初始线弹性阶段沿i(i=x,y)方向的粘滞阻尼比和自振圆频率(rad/s)。此外,非弹性体系的规一化侧向位移 (μbi)与规一化滞回位移 (μbzi)之间的关系[10-11]为式(5)~(11)。
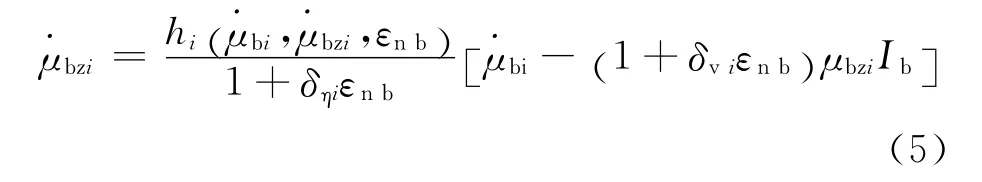
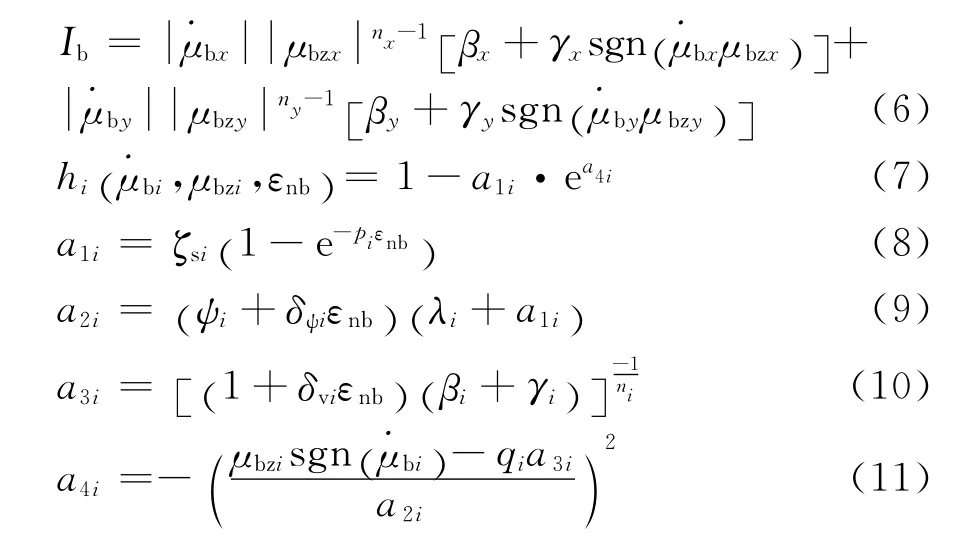
式中:βi、γi和n i为形状参数;δηi和δvi分别为刚度和强度退化参数;ζsi、p i、qi、ψi、δψi和λi为捏拢效应参数[12-13];sgn(x)为符号函数;εnb为非弹性体系在时程T内的规一化累积滞回耗能。当nx=n y=n时,εnb定义为[11]式(12)。

式中θ=tan-1(μby/μbx)为规一化侧向位移μbx和μby之间的夹角。
若引入向量 {y1,y2,y3,y4,y5,y6,y7}T={μbx,˙μbx,μby,˙μby,μbzx,μbzy,εnb}T,则可以将式(4)~(12)转换为一阶偏微分方程组(13)。
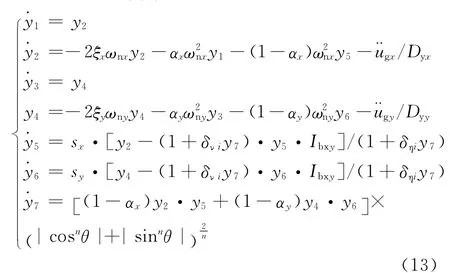
式中:
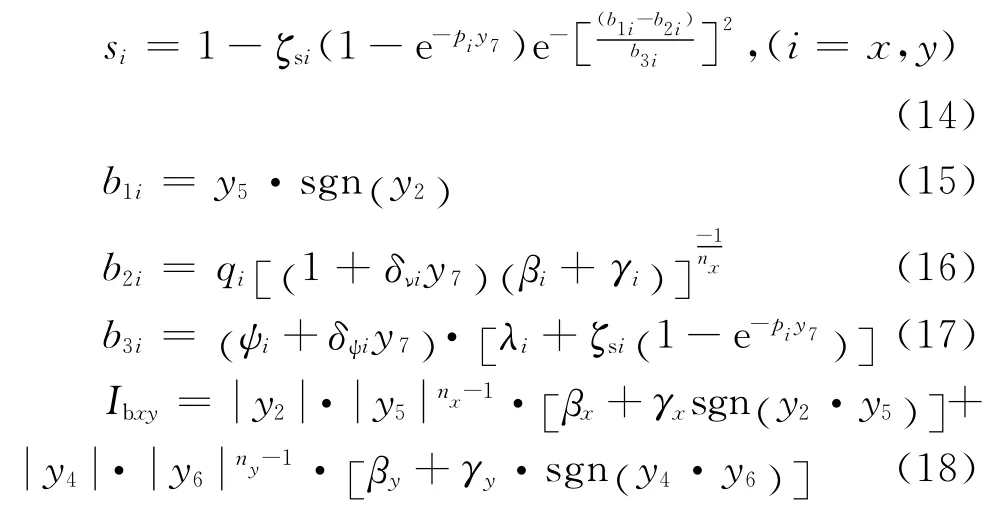
利用Gear法[14]求解式(13)所定义的偏微分方程组,可以得到规一化位移时程μbi(t)、规一化滞回位移时程μbzi(t)、规一化累积滞回耗能εnb。当nx=ny=n时,非弹性2DOF体系的地震延性需求(μb,max)和 Park-Ang地震损伤指标(Db)[11]为式(19)、(20)。

式中:δEb为循环加载的影响系数,其典型取值在0.01~0.25之间[7];μcb为单调加载下结构的延性能力。由于DPAb与μcb有关,而不同结构的μcb可能千差万别,难以统一衡量。所以本文选用Db=μcbDPAb=μb,max+δEbεnb进行分析并建立其概率预测模型,然后结合Db和目标结构的μcb,利用损伤指标DPAb=Db/μcb对特定的工程结构进行损伤评估[10]。
2 双向激励下的非弹性地震动力响应
2.1 捏拢效应和退化效应的影响
首先利用幅值递增的简谐荷载来分析捏拢效应以及强度和刚度退化对滞回曲线的影响。假定结构的自振周期Tn=1.0 s,阻尼比ξ=0.05。除图2中特别 注 明 外,模 型 参 数 {α,β,γ,n,δη,δv,ξs,p,q,ψ,δψ,λ}= {0.05,0.5,0.5,1,0,0,0,2.5,0.15,0.1,0.005,0.5}。在单向简谐荷载激励下,非弹性体系的滞回曲线如图2所示。由图2(a)可知,当刚度退化参数δη=0.15时,随着加卸载循环次数的增加,滞回曲线在加卸载过程中的切线刚度逐渐减小。由图2(b)可知,当强度退化参数δv=0.03时,随着加卸载循环次数的增加,滞回曲线的屈服强度逐渐减小。由图2(c)和图2(d)可知,当捏拢效应参数ξs=0.95时,滞回曲线在平衡位置附近出现明显的收缩效应,滞回曲线的饱满度明显下降。由此可见,该模型可以充分考虑捏拢效应、刚度退化、强度退化等因素的影响,具有较强的适用性。

图2 捏拢效应和退化效应对滞回曲线的影响
2.2 双向地震激励的影响
在双向地震激励下,非弹性体系沿一个方向的屈服或累积损伤,往往会削弱另一个方向的刚度或强度,进而明显改变非弹性体系的地震动力响应。假定结构沿x和y方向的自振周期Tnx=Tny=0.5 s,阻尼比ξx=ξy=5%,规一化屈服强度φx=φy= 0.5,模 型 参数 {αi,βi,γi,ni,δηi,δvi,ζsi,p i,qi,ψi,δψi,λi}={0.05,0.5,0.5,2,0,0,0,2.5,0.15,0.1,0.005,0.5}。上述参数均符合文献[10,13,15]的推荐取值。从NGA数据库[16]中任意选择一条地震记录进行分析。例如,由LA-Wadsworth VA Hospital South监测站所记录的1994年1月17日发生的6.69级Northridge-01地震。非弹性体系在单、双向地震激励下的滞回曲线如图3所示。图中,f i和μi分别表示单向地震激励下的规一化恢复力和规一化位移;fbi和μbi分别表示双向地震激励下的规一化恢复力和规一化位移;εnx、εny、εnbx和εnby为规一化累积滞回耗能。由图3可知,双向地震激励促使滞回曲线在卸载点附近出现明显的圆角效应;取决于地震激励和结构动力参数的特性,双向地震激励作用既可能增大也可能减小非弹性体系的累积滞回耗能。

图3 单向和双向地震激励下的滞回曲线
3 概率地震损伤指标分析
由于地震的发生以及地震加速度的传播均具有较强的随机性,所以非弹性体系的地震损伤指标也不可避免地存在随机性。下面分析双向地震激励下非弹性2DOF体系的地震损伤指标的概率统计特征。
3.1 地震记录的筛选
地震记录的选择通常需要考虑地震动对目标结构的潜在破坏势,进而根据震级、震中距、场地条件等参数从实际地震记录中选取。从美国太平洋地震工程研究中心所建立的NGA强震数据库[16]中筛选地震记录,并采用以下筛选准则[17]:1)震源位于美国加利福尼亚州;2)地震记录的场地条件为NEHRP分类[16]中的B类或C类;3)地震记录监测设备安置在自由场地或单层轻型结构的地表,即属于Geomatrix's分类[16]中的I类或A类;4)地震记录具有完整的3个加速度分量,且同时满足高通滤波器拐角频率≤0.5 Hz和低通滤波器拐角频率≥40 Hz。通过筛选,可以确定有13次地震的69条地震记录符合上述条件,见表1。

表1 从NGA数据库中筛选的69条地震记录
3.2 地震损伤指标的经验分布模型
首先确定地震损伤指标(Db)的经验分布模型。假定参数{αi,βi,γi,ni,δηi,δvi,ζsi,pi,qi,ψi,δψi,λi}={0.05,0.5,0.5,2,0,0,0,2.5,0.15,0.1,0.005,0.5}。将非弹性体系在69条地震记录作用下的Db的样本点分别描绘在Frechet和Lognormal概率纸上,如图4所示。由图4可知,当Tn=0.5 s或1.0 s时,采用Lognormal或Frechet分布来描述Db的差异性并不明显,因为Db的样本点在这2种概率纸上的分布均较好地呈现直线;当Tn=0.2 s时,采用Lognormal分布来描述Db的概率分布则更为合理,因为Db的样本点在Lognormal概率纸上的分布更趋近于直线,当规一化屈服强度较小时尤为明显。
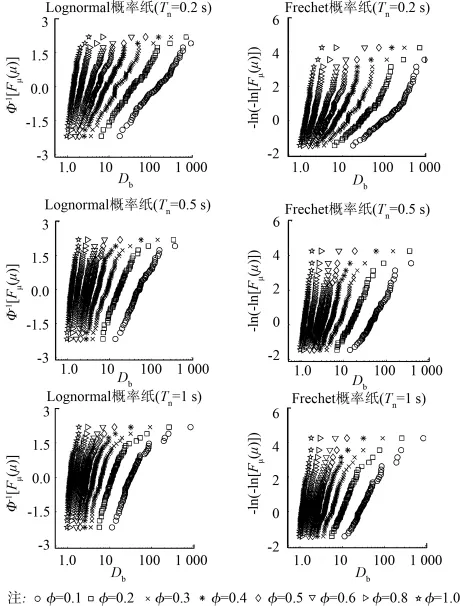
图4 D b在Lognormal和Frechet概率纸上的分布
3.3 地震损伤指标的统计特征值
下面确定地震损伤指标(Db)的统计特征值。当自振周期(Tn)为0.1、0.2、0.5、1.0或1.5 s,规一化屈服强度(φ)从0.1到0.5变化时,Db的均值和变异系数如图5所示。由图可知,Db的均值随着Tn和φ的减小而增大;随着φ的减小,Db的变异系数逐渐增大并趋于稳定,最终维持在1.0~2.0之间。
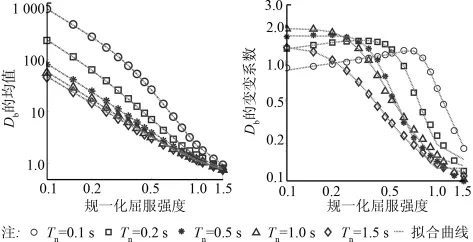
图5 D b的均值和变异系数
根据图5中的变化趋势,可以将Db的均值和变异系数的预测方程选取为[15]:

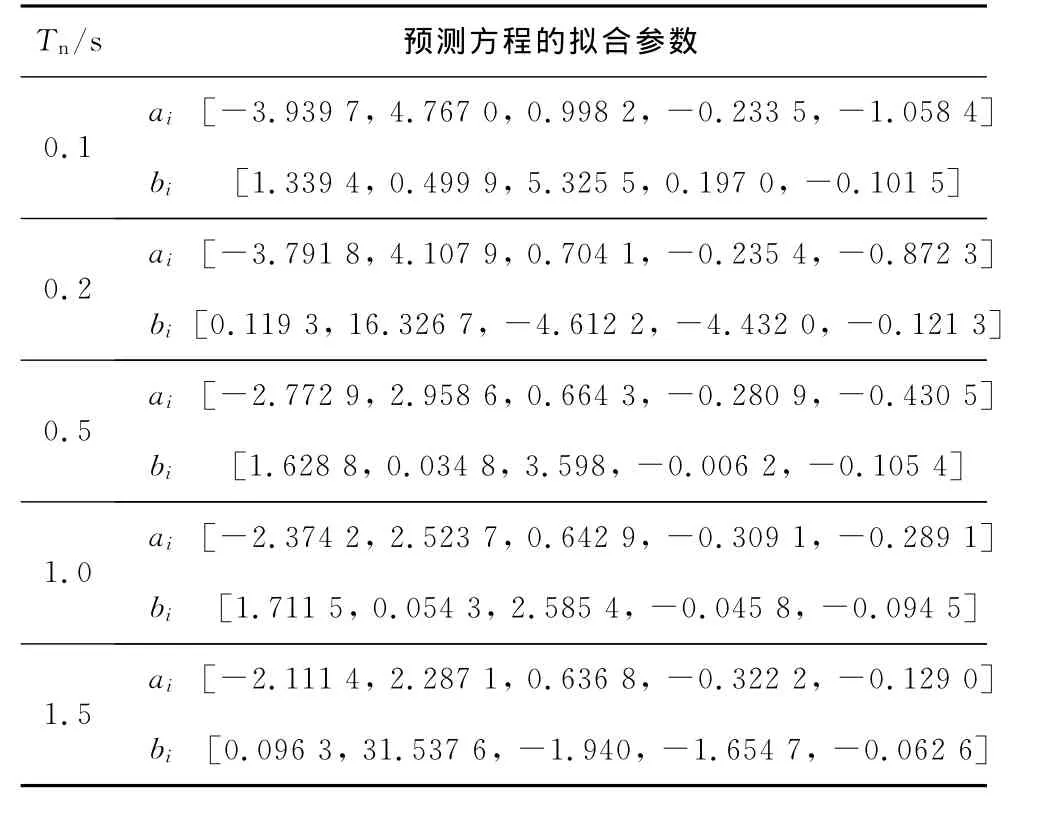
表2 预测方程的拟合参数
3.4 地震损伤指标的影响因素分析
选用表1中的69条强震记录,对20种不同情况下的地震损伤指标(Db)进行概率统计分析。假定结构的自振周期Tnx=Tny=Tn=0.5 s,规一化屈服强度φx=φy=φ=0.5,模型参数{αi,βi,ni,p i,qi,ψi,δψi,λi}={0.5,0.5,2,2.5,0.15,0.1,0.005,0.5},其他参数的取值见表3。其中,情况1为基准体系;情况2和3用于分析屈服后刚度比(αi)的影响;情况4~7考虑规一化屈服强度φx和φy的影响;情况8~11考虑自振周期(Tnx和Tny)的影响;情况12~17用于揭示强度和刚度退化参数(δvi和δηi)的影响;情况18和19用于分析捏拢效应系数(ζsi)的影响;情况20综合考虑强度退化、刚度退化和捏拢效应的影响。
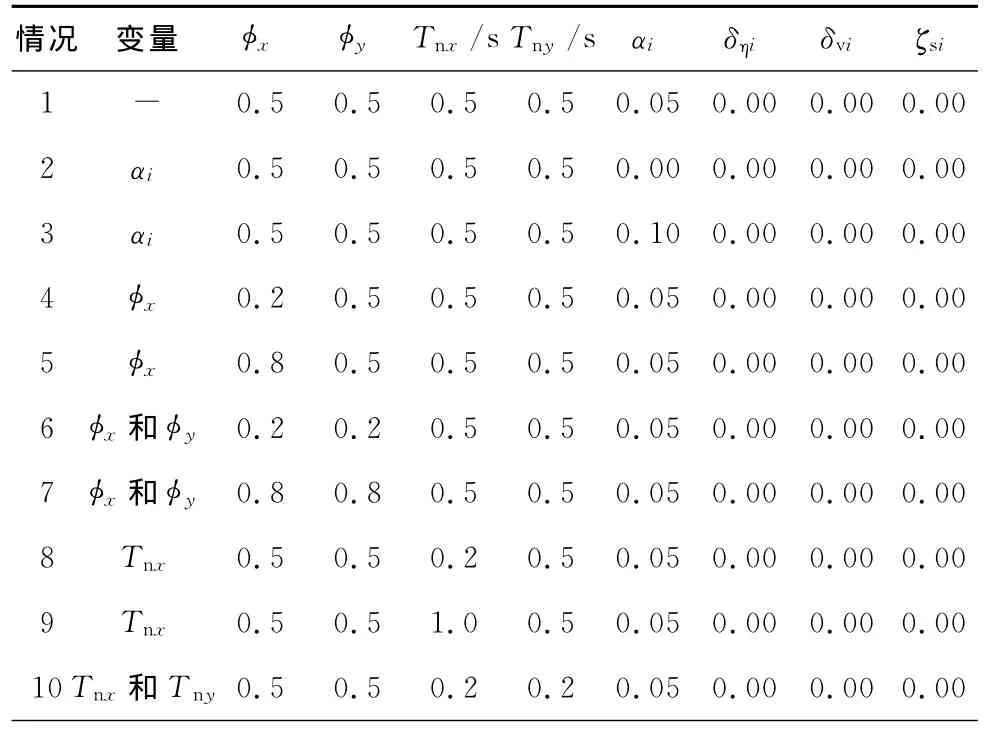
表3 在20种情况下2DOF体系的参数取值
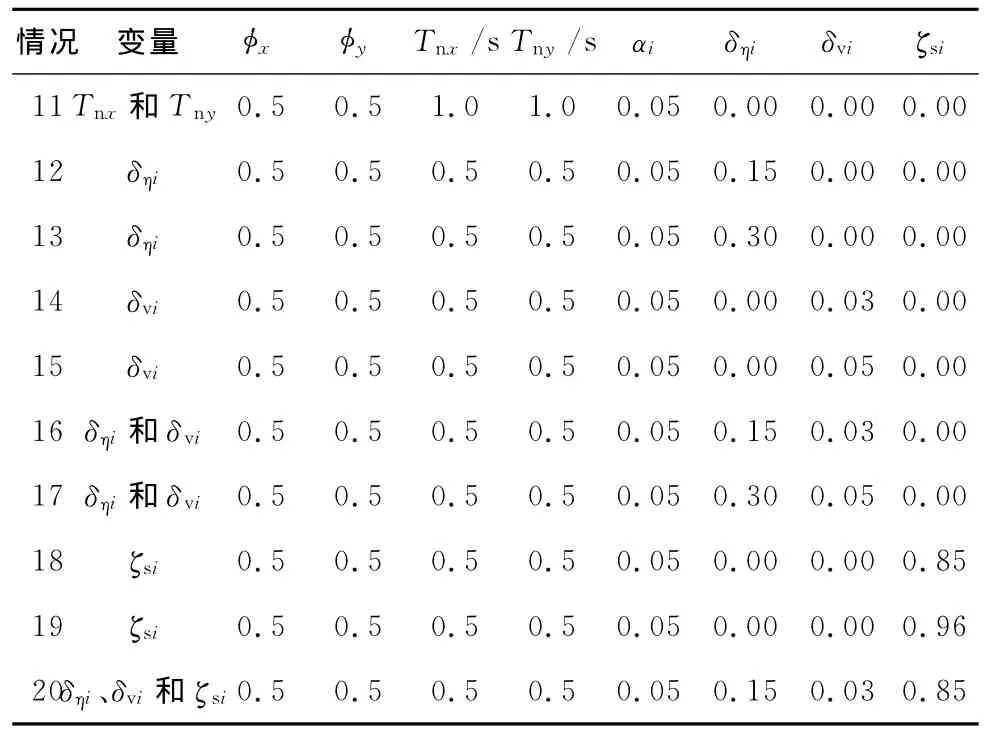
续表3
利用单向地震激励下非弹性单自由度体系的地震损伤指标(Dx和D y),可以将双向地震激励下非弹性2DOF体系的地震损伤指标近似表示为:

在69条地震记录作用下,地震损伤指标(D x,Dy,Db,Db1和Db2)的均值和变异系数分别见表4和5。为了方便比较,r1=Db/Db1和r2=Db/Db2的均值和变异系数也列于表中。由表可知,地震损伤指标(D x,D y和Db)的均值随着规一化屈服强(φi)和自振周期(Tni)的减小而增大;减小非弹性体系的规一化屈服强度(φi)和自振周期(Tni),或增大结构的强度退化系数(δvi)、刚度退化系数(δηi)和捏拢效应系数(ζsi)都会明显增大地震损伤指标的变异性;Db1为Db提供了一个近似下限值,通常低估约25%;虽然r1和r2的变异系数相似,但r2的均值比r1的均值更接近1.0,说明利用Db2来近似估计Db更为合理。也就是说,双向地震激励下非弹性2DOF体系的地震损伤指标可以近似表达为单向地震激励下非弹性单自由度体系的地震损伤指标的平方和开方。

表4 不同情况下地震损伤指标的均值
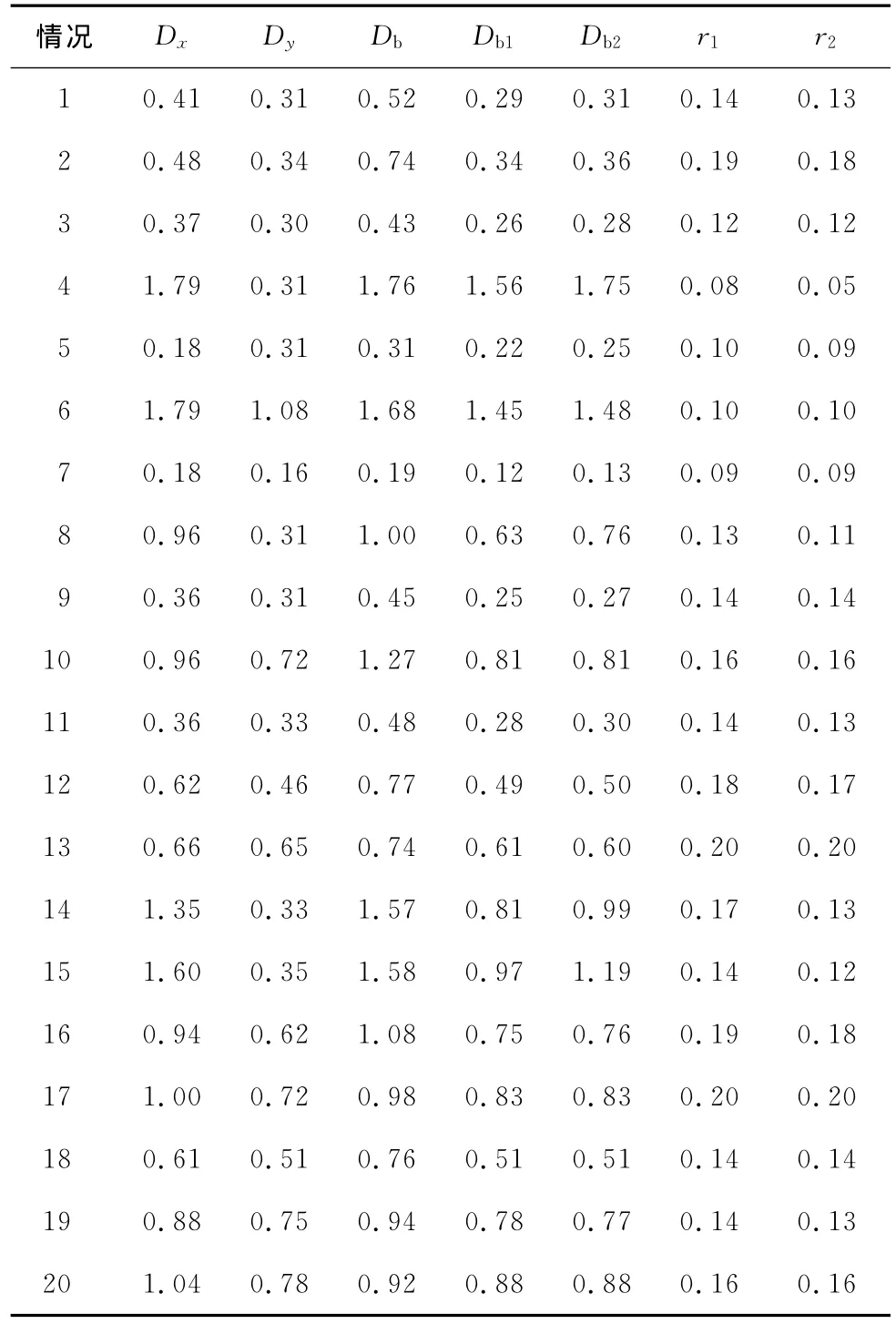
表5 不同情况下地震损伤指标的变异系数
5 结 论
综合考虑强度退化、刚度退化、捏拢效应等典型滞回特性的影响,建立了双向地震激励下非弹性2DOF体系地震损伤分析的新型数值模型。结合69条地震记录,定量地分析了非弹性2DOF体系的地震损伤指标的概率统计特征。根据计算结果可知,对于桥梁、水塔、单层或多层框架等可以模型化为集中质量体系且主要受第一阶振型控制的工程结构具有以下结论:
1)受双向恢复力耦合效应的影响,双向激励下非弹性2DOF体系的滞回曲线在卸载点附近出现明显的圆角效应,取决于地震激励和结构动力参数的特性,双向地震激励作用既可能增大也可能减小非弹性体系的累积滞回耗能。
2)在双向地震激励下,将柔性结构体系(如Tn=0.5 s或1.0 s)的地震损伤指标(Db)描述为Frechet或Lognormal分布随机变量的差异性并不明显,而将刚性结构体系(如Tn=0.2 s)的Db描述为Lognormal分布随机变量则更为合理。
3)在双向地震激励下,非弹性2DOF体系的地震损伤指标可以近似表达为单向地震激励下非弹性单自由度体系的地震损伤指标的平方和开方。
4)降低结构的屈服后刚度比或考虑强度退化、刚度退化和捏拢效应的影响,可以明显增大非弹性2DOF体系的地震损伤指标的均值和变异性。
[1]杨伟,欧进萍.基于能量原理的Park-Ang损伤模型简化计算方法[J].地震工程与工程振动,2009,29(2):159-165.YANG Wei,OU Jinping.A simplified method for computing Park-Ang damage model based on energy concept[J].Journal of Earthquake Engineering and Engineering Vibration,2009,29(2):159-165.
[2]Park Y J,Ang A H S.Mechanistic seismic damage model for reinforced concrete[J].Journal of Structural Engineering,ASCE,1985,111(4):722-739.
[3]Park Y J,Ang A H S,Wen Y K.Seismic damage analysis of reinforced concrete buildings[J].Journal of structural Engineering,ASCE,1985,111(4):740-757.
[4]王东升,冯启民,王国新.考虑低周疲劳寿命的改进Park-Ang地震损伤模型[J].土木工程学报,2004,37(11):41-49.WANG Dongsheng,FENG Qimin,WANG Guoxin.A modified Park-Ang seismic damage model considering low cycle fatigue life [J].China Civil Engineering Journal,2004,37(11):41-49.
[5]于琦,孟少平,吴京.基于变形与能量双重准则的钢筋混凝土结构地震损伤评估[J].土木工程学报,2011,44(5):16-23.YU Qi,MENG Shaoping,WU Jing.Deformation and energy based seismic damage evaluation of reinforced concrete structures [J].China Civil Engineering Journal,2011,44(5):16-23.
[6]易伟建,尹犟.基于位移及滞回耗能的结构抗震性能评估新方法[J].湖南大学学报:自然科学版,2009,36(8):1-6.YI Weijian,YIN Jiang.A new method for evaluating seismic performance based on displacement and hysteretic energy [J].Journal of Hunan University:Natural Sciences,2009,36(8):1-6.
[7]Ghosh S,Datta D,Katakdhond A A.Estimation of the Park-Ang damage index for planar multi-storey frames using equivalent single degree systems[J].Engineering Structures,2011,33(9):2509-2524.
[8]张国军,吕西林.高强混凝土框架柱的地震损伤模型[J].地震工程与工程振动,2005,25(2):100-104.ZHANG Guojun,LYU Xilin.Seismic damage model of high strength reinforced concrete frame columns[J].Journal of Earthquake Engineering and Engineering Vibration,2005,25(2):100-104.
[9]傅剑平,王敏,白绍良.对用于钢筋混凝土结构的Park-Ang双参数破坏准则的识别和修正[J].地震工程与工程振动,2005,25(5):73-79.FU Jianping,WANG Min,BAI Shaoliang.Identification and modification of the Park-Ang criterion for failure of RC structures[J].Journal of Earthquake Engineering and Engineering Vibration,2005,25(5):73-79.
[10]Goda K, Hong H P,Lee C S.Probabilistic characteristics of seismic ductility demand of SDOF systems with Bouc-Wen hysteretic behavior[J].Journal of Earthquake Engineering,2009,13(5):600-622.
[11]Lee C S,Hong H P.Statistics of inelastic responses of hysteretic systems under bidirectional seismic excitations[J].Engineering Structures,2010,32(8):2074-2086.
[12]Ajavakom N,Ng C H,Ma F.Performance of nonlinear degrading structures:identification,validation,and prediction[J].Computers &Structures,2008,86(7/8):652-662.
[13]Ma F,Zhang H,Bockstedte A,et al.Parameter analysis of the differential model of hysteresis[J].Journal of Applied Mechanics Ransactions of the ASME,2004,71(3):342-349.
[14]Shampine L F,Reichelt M W.The matlab ode suite[J].Siam Journal of Scientific Computing,1997,18(1):1-22.
[15]余波,刘陶钧,洪汉平.捏拢效应与P-Δ效应对延性需求和损伤指标的影响[J].地震工程与工程振动,2011,31(4):94-105.YU Bo,LIU Taojun,HONG Hanping.Influences of pinching and P-Δeffects on seismic ductility demand and damage index[J].Journal of Earthquake Engineering and Engineering Vibration,2011,31(4):94-105.
[16]Pacific Earthquake Engineering Research (PEER)Center.Next generation attenuation database[D/OL].http://peer.berkeley.edu/nga/index.html.
[17]Hong H P,Goda K.Orientation dependent ground motion measure for seismic hazard assessment [J].Bulletin of the Seismological Society of America,2007,97:1525-1538.

