自适应-自适应波束形成的零陷加深技术

朱德智，代月花

(1.中国电子科技集团第三十八研究所，合肥 230088;2.安徽大学 电子信息工程学院，合肥 230061)

0 引言

自适应波束形成是雷达抗干扰的一种重要方法。通过自适应波束形成，使雷达发射方向图或接收方向图在干扰方向形成零陷，以削弱干扰信号对雷达目标检测能力的影响。对于大型阵列雷达，阵元域自适应波束形成的运算量过大，工程上难以实现，而波束域自适应波束形成则可以解决这一问题。在波束域自适应波束形成中，自适应-自适应波束形成(A-A DBF）方法是一种既能最大限度地降低运算量，又能保证波束在干扰方向外不发生畸变的方法［1-2］。但是，在干扰起伏较大的干扰环境下，统计得到的信号协方差矩阵中的干扰分量常常低于被处理信号中的干扰分量［3-4］，导致因自适应波束方向图零点较浅而不能完全对消干扰，使雷达抗干扰性能和目标检测性能受到影响。

为克服这一缺陷，本文给出了一种零陷加深处理方法，使采集的样本中干扰信号较弱时自适应-自适应波束形成仍能有较深零陷，以对抗较强的干扰信号。

1 自适应-自适应波束形成

A-A DBF处理首先估计干扰的方向，然后在各干扰方向和观测方向分别形成各干扰波束和主波束，并利用干扰波束和主波束进行自适应处理。图1为A-A DBF处理结构图。

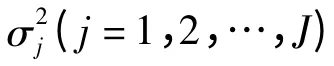
图1 自适应-自适应波束形成处理结构图

阵列接收到的信号可以表示为

式中，a(θj），j=1，…，J为干扰信号的导向矢量，a(θj）=［1，e－j2πdsin(θj）/λ，…，e－j2π(M－1）dsin(θj）/λ］T，N(t）=［n1(t），n2(t），…，nM(t）］T为噪声矢量，sj(t）为第j个干扰信号。

干扰波束j的输出为

主波束的输出为

其中，a(θB）=［1，e－j2πdsin(θB）/λ，…，e－j2π(M－1）dsin(θB）/λ］T，θB为主波束的方向。

自适应处理按照式(4）处理:

其中，aAA(θB），RAA按照下式计算:

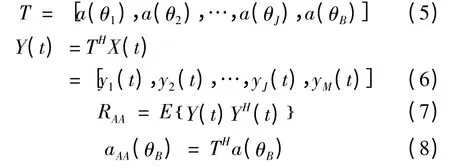
自适应波束形成的输出为

式(7）中，相关矩阵的维数为J+1。由于空间干扰数是有限的，对于大型阵列雷达，相关矩阵的维数远小于阵元数，运算量大幅降低。同时，A-A DBF 输出信噪比较全自适应法几乎没有损失，并且收敛特性优于全自适应法。

2 自适应-自适应波束形成零陷加深技术

自适应波束形成的零点深度受到用于计算自适应权系数的样本中干扰分量的强度影响。样本中的干扰分量越强，自适应波束方向图在干扰方向的零点越深，抗干扰能力越强［5］。为了使自适应波束形成的零陷加深，考虑提取形成相关矩阵的采样信号中的干扰分量，并乘以一定的权值后加到采样信号中，以达到加强信号中干扰分量的目的。为此，首先分析协方差矩阵的特征结构。

对于常规自适应波束形成，阵列的协方差矩阵为

根据式(1）:

由于各干扰信号之间及干扰与噪声之间互不相干，有

其中Rint和Rn分别为干扰相关矩阵和噪声相关矩阵:

根据特征分解理论，a(θj），j=1，…，J 构成信号子空间［6，7］。

对于A-A DBF，根据式(6）和(7）有

和常规自适应波束形成类似，A-A DBF的相关矩阵也可以进行特征分解:

综合式(12）～(16），有

同样，根据特征分解理论，THa(θj），j=1，…，J 构成RAA的信号子空间，即RAA的信号子空间为

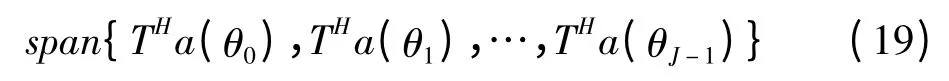
记AAA=TH［a(θ1），a(θ2），…，a(θJ）］=THA，信号子空间的投影矩阵P为

将Y(t）向信号子空间投影，结果乘以权值g后与Y(t）相加，可以得到干扰加强的波束域采样向量:［8］

由干扰加强的波束域采样向量构建干扰加强的采样矩阵，并用于自适应波束形成，得到

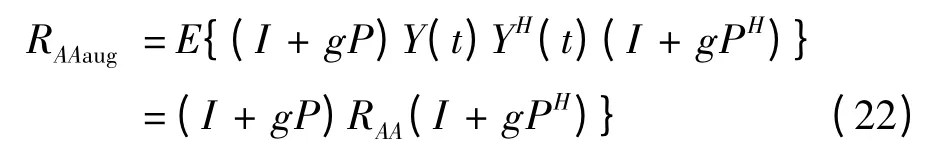
自适应-自适应波束形成的权系数变为

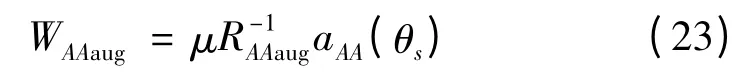
其中aAA(θs）=THa(θs）。

波束形成的输出为

3 性能分析及计算机仿真

考虑一均匀直线阵(ULA），阵元个数M=100，阵元间距为半波长。空间存在两个互不相干的白噪声干扰信号，干扰方向分别为－2.5°和2.5°，干扰幅度随机变化。各接收通道的噪声为高斯白噪声。为对抗干扰，在波束的期望方向和2个干扰方向分别形成波束，并采用零陷加深的A-A DBF。

3.1 波束方向图

图2～图5分别给出了在两个干扰的干噪比均为－20 dB时不经过零陷加深处理和g分别为0.5、1.0、10.0的零陷加深自适应-自适应波束形成的方向图。由于在用于计算自适应权系数的采样数据中干扰信号强度弱，未经零陷加深的自适应-自适应波束形成零点较浅;采用零陷加深处理后，随着g 值的增加，两个干扰方向的零点逐渐加深，波束形成的抗干扰能力增强。

3.2 对抗幅度起伏干扰的性能

对于所给阵列及干扰环境下，在0°方向上有一多普勒频率为1 kHz的目标，目标信号的信噪比为－25 dB。雷达发射相参脉冲信号，并对回波进行自适应波束形成和滤波处理。假定自适应波束形成数据采集的时刻2个干扰信号的干噪比均为－20 dB，随后干扰信号增大至20 dB。分别利用常规自适应-自适应波束形成和零陷加深的自适应-自适应波束形成进行处理，结果示于图6～图9，其中图6为常规A-A DBF 结果，图7～图9为g分别为0.5、1.0和10.0时的零陷加深AA DBF 结果。从图中可以看出，常规A-A DBF的干扰对消性能差，干扰信号剩余很多，信号被淹没在干扰信号中;采用零陷加深技术后，干扰对消性能增强，干扰剩余量随着g 值的增大而减小，信干噪比逐渐增加，目标的检测概率逐渐提高。

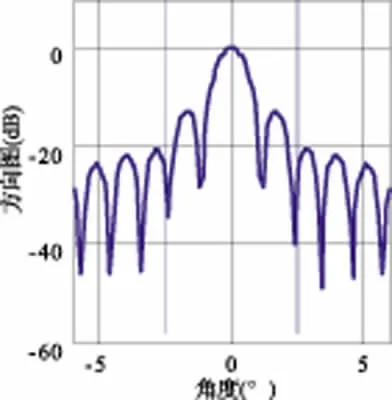
图2 常规A-A波束形成方向图

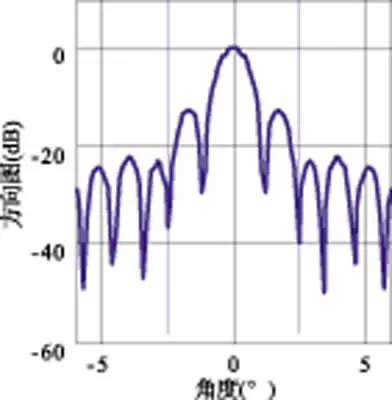
图3 零陷加深A-A 法方向图(g=0.5）

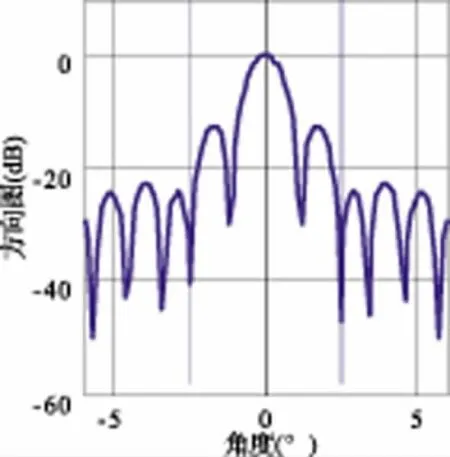
图4 零陷加深A-A 法方向图(g=1.0）

图5 零陷加深A-A 法方向图(g=10.0）

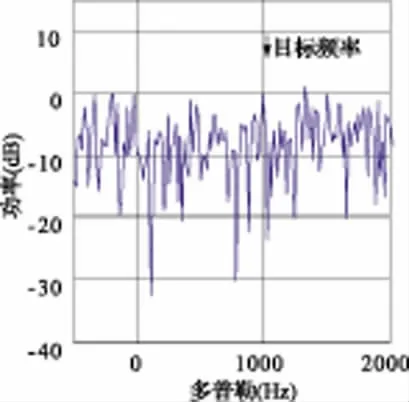
图6 常规A-A 法处理结果

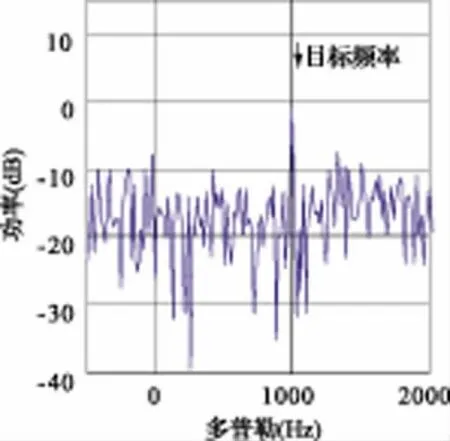
图7 零陷加深A-A 法处理结果(g=0.5）

图8 零陷加深A-A 法处理结果(g=1.0）

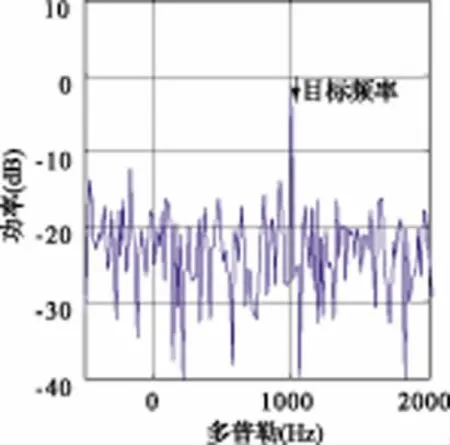
图9 零陷加深A-A 法处理结果(g=10.0）

4 结束语

A-A DBF 是一种能大幅降低运算量的自适应波束形成方法，对于中型和大型阵列雷达，该方法具有明显的优越性。但是，在干扰功率起伏的电磁环境中，A-A DBF和其他方法一样，存在抗干扰性能下降的问题。本文给出了一种先增强用于计算协方差矩阵的信号中的干扰分量再进行自适应处理的方法。本方法在形成协方差矩阵的采样信号中的干扰分量相对很弱的情况下仍能很好地对消强干扰信号，使系统抗干扰性能大幅提高。

［1］E Brooker，J M Howell.Adaptive-Adaptive Array Processing［J］.Proceedings of the IEEE，1986，74(4）:602-604.

［2］Huaijin Gu.Angle-tracking adaptive array-adaptive-adaptive array processing［J］.Radar conference of the IEEE，2007:750-755.

［3］Geoffrey C Street，Dr.Kristine Bell.Characterization of LMS and DMR Beamformers in the Presence of Loud Periodic Interferers ［C］//Proceed-ings of the Adaptive Sensor Array Processing Workshop，Lexington，MA，USA，1999:19-24.

［4］Li Wen-xing，Li Yi-peng.An Effective Method on Increasing the Null Depth of Beam forming via Virtual Array Transformation ［C］//Information Science and Engineering，Hangzhou，China，2010:973-976.

［5］Dimitri G，Manolakis，Vinay K Ingle，Stephen M Kogon.Statistical and Adaptive Signal Processing［M］.Artech House Publishers，2005:648.

［6］Li Wen-xing，Li Yi-peng.An Effective Method on Increasing the Null Depth of Beam forming via Virtual Array Transformation［C］// Information Science and Engineering，Hangzhou，China，2010:973-976.

［7］2-D DOA Estimation for Local Scattered CDMA Signals by Modified Fastica in Colored non-Gaussian Noise［J］.Journal of the Chinese Institute of Engineers，2008，31(4）:691-696.

［8］W Wang，L R Wyatt.Radio frequency interference cancellation for sea-state remote sensing by high frequency radar ［J］.IET Radar Sonar Array，2011，5(4）:405-415.