利用MATLAB图形技术实现麦克斯韦速度分布律教学可视化

叶剑锋

（黄山学院 信息工程学院，安徽 黄山 245041）

麦克斯韦速度（速率）分布律是热学气体动理论教学中的很重要的内容，是研究气体分子热运动、气体分子碰撞及其气体输运过程的理论依据。但其速度分布函数和速率分布函数分别是速度分量的三元高斯函数和速率的一元高斯函数与速率的二次函数的乘积，函数关系比较复杂。而且随着不同的气体及所处平衡态温度的变化，速度、速率分布的精确计算和分布曲面、曲线的精确绘制变得比较繁杂而不易操作。以往的热学教学中教师往往都代之以草图，降低了科学性。本文用MATLAB绘图和模拟能力用于麦克斯韦速度（速率）分布函数的教学和研究中，提高了教学效果。

1 麦克斯韦速度（速率）分布律

麦克斯韦速度分布律是在平衡状态下，当气体分子间的相互作用可以忽略时,分布在速度区间vxvx+dvx，vy-vy+duy，vz-vz+dvz内的分子比率为

其中N为气体分子总数；dN为分布在上述速度区间内的分子数；m为单个分子的质量；k为玻尔兹曼常数；T为气体处于平衡态时的热力学温度。

当只考虑速度的大小而不考虑速度的方向时，速度分布率蜕化为速率分布律，可表述为：

在平衡状态下，当气体分子间的相互作用可以忽略时，分布在任意速率区间v-v+dv内的分子数比率为

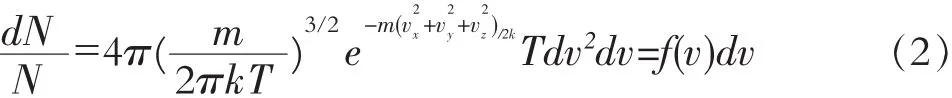
（1），（2）两式中

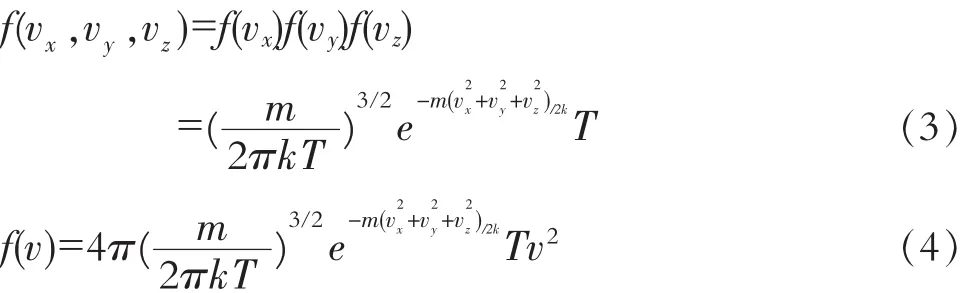
分别称为麦克斯韦速度分布函数和速率分布函数，其物理意义分别表示分布在单位速度区间或单位速率区间内的分子数比率。[1]

2 基于MATLAB的麦氏分布律的可视化

2.1 不同气体在同一温度下的麦克斯韦速度分布律

利用MATLAB编程模拟氢气、氮气、氧气和二氧化碳在同一温度（T=300K）时的麦克斯韦速度分布函数曲面，程序如下:

图 1只展示了f(vx，vy）随速度分量 vx，vy变化的曲面，完整速度分布函数 f（vx，vy，vz）=f（vx）f（vy）f（vz）应是个四维形式，即f（vx，vy，vz）随 3 个速率分量vx，vy，vz变化，但四维无法用坐标形式标出。同样可以做出 f（vx，vz），f（vy，vz），分布面，利用速度分布函数 f（vx，vy）随速度vx，vy分量变化的三维情形即可以联想到四维情形。[2]

2.2 同一气体在不同温度下的麦克斯韦速度分布律

利用MATLAB 同样绘制出氢气在温度为300K、600K、900K、1200K时的麦克斯韦速度分布函数曲面如图2所示，程序如下：

虽然不同温度下的曲面形式不变，但是通过观察f（vx，vy）轴可见相同的vx，vy时，f（vx，vy）值会随着温度提升而增加。

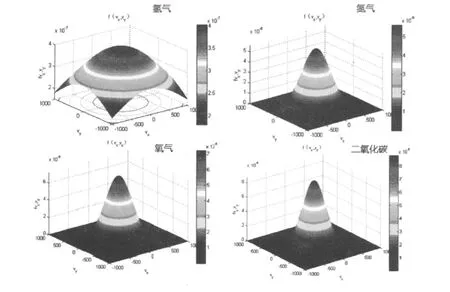
图1 同一温度下不同气体的速度分布函数

图2 同一气体在不同温度下速度分布函数

2.3 不同气体同一温度下的麦克斯韦速率分布律

麦克斯韦速率分布函数f（v）是一个二维形式。图3为氢气、氮气、氧气和二氧化碳等4种气体在相同的温度（T=300K）时的麦克斯韦速度分布函数曲线，程序为：

由图3可以清晰的看到由于分布函数满足归一化结果，随着气体分子量的增大，其统计速率变化的趋势递减，速率分布的密度加重，其最可几速率减小。

2.4 同一气体在不同温度下的麦克斯韦速率分布律

同一气体氢气在不同温度（300K、600K、900K 1200K）时的麦克斯韦速度分布函数曲线如图4所示，程序为：

图4清晰显示，随着温度的上升，氢气的最可几速率增加，在归一化条件的约束下，其速度变化趋势增加。[3]

3 结束语

结合MATLAB编程绘图功能，讨论了同种气体在不同温度下及其不同气体在同一温度下的麦克斯韦速度（速率）的可视化，能够使抽象的麦克斯韦速度（速率）分布规律，变得具体、形象、生动，易于让学生掌握速率分布曲线具体内容；MATLAB为热学教学提供了简捷直观的途径，便于学习者对于物理的原理、概念、公式和图像作深入了解。[4]

[1]秦允豪.热学[M].北京：高等教育出版社,2004：58-63.

[2]彭芳麟.数学物理方程的MATLAB解法与可视化[M].北京：清华大学出版社,2004：85-153.

[3]王向贤,朱浩瑞.基于MATALB的麦克斯韦速率分布函数的数字化教学[J].宜春学院学报，2011,33(4)：17-19.

[4]王明美.MATALB在麦克斯韦速率分布律教学中的应用[J].合肥师范学院学报,2010,28(6)：40-42.