基于分形损失理论的粗糙节理岩体中应力波波速研究

李业学，谢向东，秦 丽

(1.襄樊学院 建筑工程学院，湖北 襄樊 410053;2.四川大学 水利水电学院，成都 610065)

爆破仍然是当今世界在地下开采过程中采用的最为广泛的方法之一。爆炸所释放的能量部分用于破岩，部分则以应力波形式自爆源向外传播，遭遇裂缝、节理等不连续结构面后，将产生复杂的应力状态，对工程体与地质体的安全可能造成隐患，因而，为了达到防患于未然的目的，深入探讨节理对应力波传播的影响规律就显得很有必要。

许多研究者［1－5］探讨了岩石特性和声波波速的相互关系，发现这两者密切相关，存在大量影响岩石中应力波波速的因素，这些因素大致可以包括:岩石种类、密度、颗粒尺度和形状、空隙率、各项异性、空隙水、裂隙断层不连续结构面、围压和温度。其中，岩石中包含的节理是影响应力波波速的主要因素之一。

学者们通过分析岩石中微裂隙、结构等特点，探讨了描述节理的各参量对应力波波速的影响规律，比较有代表性的有:Oda［6－7］从岩体节理、裂隙的角度提出了用裂隙张量来表示岩体中裂隙的几何形态(裂隙的密度、尺寸和方向)的方法，并建立了裂隙张量与波速之间的关系。文献［8］提出了考虑裂纹宽度影响的波速计算方法。文献［9］将节理划分为微观节理与宏观节理，分别探讨了它们对应力波波速的影响规律，类似的研究还有［10－12］。研究者们已经就节理对波速的影响这一问题做了大量有意义的工作，并取得了丰硕的研究成果，但纵观以上研究，他们的研究工作均基于节理面光滑这一假定，事实上，经过亿万年成岩过程形成的岩石，所包含的节理可以说必然粗糙不平，为了研究成果更贴近工程实际，力学家们继续探讨了节理面几何构型对应力波传播的影响规律。比较有代表性的有，文献［13］通过在岩石表面纵横刻画刻痕模拟节理面的粗糙性，探讨了应力波波速与节理面粗糙性的关系;但是，该文献描述粗糙节理构型参数(节理粗糙度系数FRC)是作者规定的，存在着大量经验方法，这些在理论是上不完善的至少是不可接受的，随着分形几何的诞生，其几何构型通常采用分形维数来描述。

分形维数计算理论自分形几何由Mandelbrot［14］创立以来，其研究在短短数十年间就取得了累累硕果，从三角形棱柱法［15］，投影覆盖法［16］，立方体覆盖法［17］直至改进立方体覆盖法［18］，计算方法在理论上可以说已经发展到了近乎完美的地步，但是维数计算过程中存在瓶颈—激光表面仪的使用。该仪器的扫描视野有限，相对巨大尺度的工程体经常显得无能为力，因而，学者们随后探讨了粗糙表面维数的间接计算法——图像维数，如:二值化图像维数［19］，灰度图像维数［20］，在一定程度上缓解了这一困难，但问题的关键在于现实生活中的图像是真彩图，二值化图像与灰度图像仅仅是真彩图像的理想状态与简化结果。因而，为了使研究成果更切合工程实际，探讨真彩图像的维数计算方法势在必行。

本文拟定探讨真彩图像维数的计算方法，提出相应计算理论，并基于损伤理论推导应力波在节理岩石中传播波速的解析解，建立图像维数与应力波波速间的关系。

1 应力波穿越分形节理时的波速

在三维一般情况下，当忽略体力影响时，运动方程可表示为:

其中:Vi(i=X、Y、Z)为质点速度，σmn(m，n=X、Y、Z)为应力;ρ是体积密度。对于均匀，各向同性，线弹性介质，可利用Lame形式的Hooke定律代入后消除一些参数，然而，众所周知，通过亿万年成岩过程形成的岩石内部包含大量微孔隙，裂纹，夹杂甚至宏观裂缝等一系列不连续结构面，它不可能是一种理想的均质各向同性体，显然并不满足Hooke定律的应用条件，一条可行的措施是将包含节理的岩石材料从几何构型与物理性质上进行等效，使之满足Hooke定律应用条件，必须注意的是:在理论推导过程中，所有参数必须代之以对应的等效物理参数。基于上述等效假定可得:

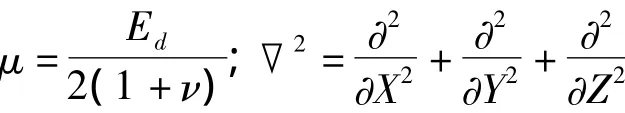
其中:μ、λ 为 lame常数;εij(i，j=X，Y，Z)为应变;ν为泊松比。uX、uY、uZ为对应位移分量。

对式(2)中三个式子分别对X，Y，Z微分再相加则可得:

这是对体积膨胀Δ的线性双曲型偏微分方程，表示体积膨胀Δ以波速Vp传播，即:

上式也可写为:

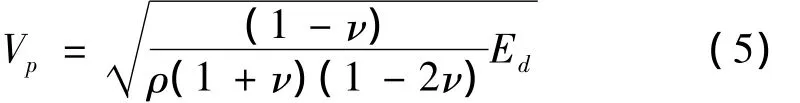
其中:Vp为应力波波速;Ed为有效弹模。

岩体内包含大量不连续结构面，或者说岩石材料存在一定程度的损伤，且材料损伤演化具有分形性质［16，17］，因而本文结合损伤力学原理与分形理论，给出了一种兼顾损伤细观特征描述和宏观损伤力学分析需要的分形损伤变量ω(d，δ)，可以表示为:

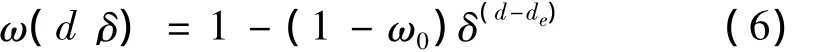
其中ω0是欧氏空间表观损伤变量;d为节理面分形维数;de为典型域的Euclidean维数;δ是量测尺度。由于实际粗糙岩石表面在Euclidean空间中非二维的面，而是三维的体，故其欧式维数应该是3，即de=3，所以有:

引入损伤变量后，有效动态弹性模量可表示为:

其中Ed0为初始弹模。

将式(7)代入式(8)得:

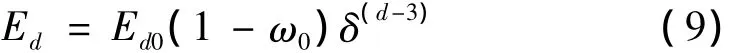
将式(8)代入式(5)得:

依据上式，我们考虑两种极限情况，其一，如果岩石材料处于理想的完整状态，或者说没有出现损伤状态，此时有:

另外，依据分形理论，当材料内没有孔隙、裂纹等不连续结构面存在时，此时的岩石材料在分形空间中的维数为3，即:

将式 (11)、式(12)代入式(10)可得:

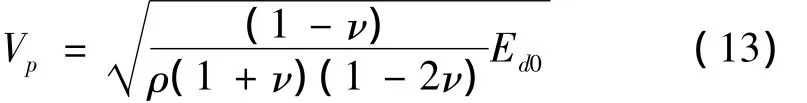
分析式(13)可知，此式正是通过经典弹性波理论导出的应力波波速计算公式。

考虑另外一个极限情况，岩石完全开裂，即发生了完全损伤，此时岩石损伤程度为:

将式(14)代入式(10)可得:

式(15)表明，应力波不能穿越完全开裂的岩石，这与实际情况是完全相符的。

通过极限状态分析可知，本文基于分形损伤理论导出的应力波波速的解析解是经典理论公式的推广，在实际工程中将更具有普适性，而在经典弹性理论框架内推导出的应力波速计算公式是分形空间中波速公式在理想状态下的特例。

2 参数研究

为了揭示波速随着表面维数变化而改变的规律性，从式(10)不难看出，必须分别探讨粗糙表面分形维数与表观损伤变量的计算方法。以下各自给出上述两参量(维数、表观损伤变量)的计算过程，并由此导出考虑节理面分形效应的应力波波速。

2.1 节理面图像分形维数计算

工程尺度上的节理大小通常大大超出激光表面仪的扫描视野，使得计算节理面维数存在很大困难，这往往可能成为探讨粗糙节理对应力波波速影响规律的瓶颈。为了克服上述困难，本文在描述节理粗糙度时采用节理面图像维数替换“普通”节理面维数，以下探讨真彩图像维数计算的相关理论。

2.1.1 颜色表面的模型构建

如图1所示，RGB颜色模型是一个加色模型，多种基色的强度加在一起生成一种颜色。颜色单元体边界中的每一个颜色点可表示一个三元组(R，G，B)，三分量R、G、B取值范围均在区间［0，1］内。依据这一模型，任何一种颜色 Cλ在 RGB坐标中可表示为如下矢量:

图1 颜色单元体Fig.1 Color units

一副图象由多个象素点构成，每一象素点对应一种RGB模式的颜色，由于任何一种RGB颜色可表示为形如式(16)的矢量，所以，在每个象素点处均可构建一个三维矢量，如:矢量 Aa、Bb、Cc、Dd(见图 2)。连接各矢量的终端组成2～3维的粗糙曲面(如图2)，即为所构建的颜色表面。

2.1.2 真彩图象分维计算方法

由上述的颜色表面构建程序可以看到，每个象素点与该象素点R、G、B值所构建的矢量都是以各自象素点所在位置为坐标原点，各矢量所在的坐标空间不统一，因而有必要将所有矢量统一至同一坐标系下。具体算法如下:

(1)对图象所在平面进行网格剖分，网格间距选为象素间距δ;

(2)建立如图1所示坐标系统，坐标原点设在A点，其中，详图1中A、B、C、D四点在该坐标系下的坐标分别为(iδ，jδ，0)、((i+1)δ，jδ，0)、(iδ，(j+1)δ，0)、((i+1)δ，(j+1)δ，0)，所以，颜色表面上对应的 a、b、c、d 四点坐标分别是:(Ra+iδ，Ga+jδ，Ba)、(Rb+(i+1)δ，Gb+jδ，Bb)、(Rc+iδ，Gc+(j+1)δ，Bc)、(Rd+(i+1)δ，Gd+(j+1)δ，Bd)。由此可得:颜色表面上任一点的坐标在统一坐标系下可表示为:(R+i·δ，G+j·δ，B)(i=0，1，2…m，j=0，1，2…n)(m 与 n 分别为网格点的行列数)。依据上述方法，我们获取了粗糙颜色表面的三维坐标。

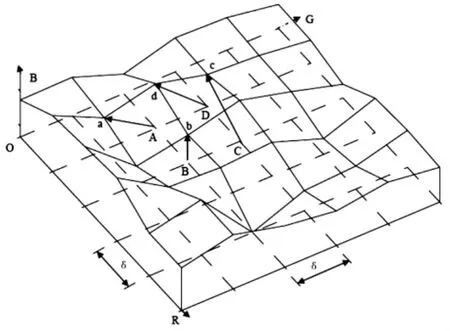
图2 颜色表面示意图Fig.2 Schematic figure on color surface

2.1.3 图像维数计算

由颜色表面构建过程不难知道，颜色表面上的点分布不均匀，在分析该颜色表面的分形特性前，有必要利用泛克里金法对三维坐标数据网格化。基于周宏伟［21］提出的分形维数计算理论－立方体覆盖法，计算其分形维数，该分维即为真彩图象分形维数。具体过程如下:如图3所示，在平面XOY上存在一正方形网格，网格尺寸为δ，正方形的四个角点处分别对应四个高度 h(i，j)，h(i，j+1)、h(i+1，j)和 h(i+1，j+1)(1≤i，j≤n－1，n为每个边的量测点数)。用边长为δ的立方体对粗糙颜色表面进行覆盖，计算覆盖区域δ×δ内的立方体个数，即在第i，j网格内，覆盖粗糙面的立方体个数 Gi，j为:

式中INT为取整函数。

则覆盖整个粗糙颜色表面所需的立方体总数为:

改变观测尺度再次覆盖粗糙颜色表面，计算覆盖整个表面所需的立方体总数，若粗糙颜色表面具有分形性质，按分形理论，立方体总数G(δ)与尺度δ之间存在如下关系:

式中D为粗糙颜色表面自相似分形维数。

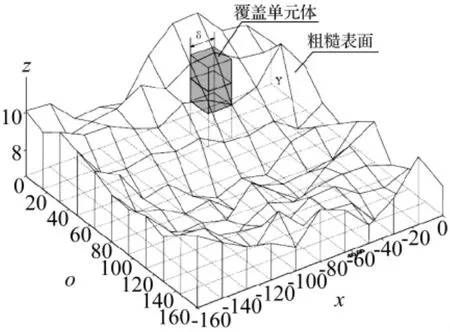
图3 立方体覆盖法Fig.3 Cubic covering method

基于上述原理，本文计算了所有节理面图像维数(见表2)，限于篇幅，本文仅给出了一组典型的岩石节理表面图像及其对应的粗糙颜色表面形貌图、维数计算的log－log图(见图4)。其中δ指量测尺度;G是覆盖盒子总数。

2.2 表观损伤变量

依据损伤力学的相关理论，本文的表观损伤变量采用缺陷体积与名义体积之比这一定义，即:

其中:V为缺陷体积，V0为名义体积，V为损伤后的体积。

对三维坐标数据中的高度坐标进行纵横方向搜索，找出高度值中的最大者与最小者，即:

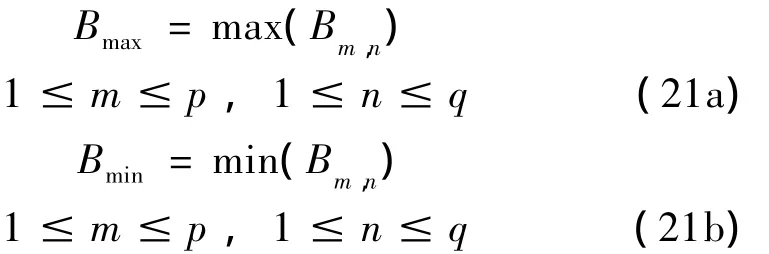
图4 7#岩石节理面图像、对应颜色表面图、维数计算log-log图Fig.4 Image of 7#rock joint surface，picture of corresponding color surface and bi－ logarithm plot used to computer dimension

其中p，q分别为纵横方向上的扫描点数。

名义体积可表示为:

由扫描坐标可求得岩石损伤后的体积:

将式(22)、式(23)代入式(20)可得:

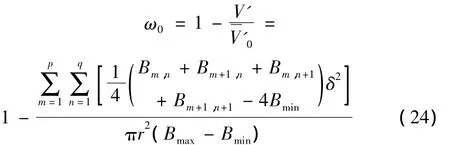
2.3 应力波波速的计算

在除预制裂纹外岩样内其它部分致密且均质这一假定近似满足的前提下，一组岩样损伤程度不断增加，可等效认为是某一个岩样损伤的动态持续增大，因此存在一个没有损伤或损伤度较小的初始状态，取此状态的弹性模量作为弹模的计算初始值。为了计算便利，并考虑计算精度要求，本文采用没有预制裂纹的致密花岗岩的弹模，作为岩样损伤演化过程中的初始值Ed0。其它计算参数(如:体积密度)通过常规试验测定，具体见表1，将表中参数代入公式(10)，即可求得考虑节理面图像分形效应后的应力波波速(见表2)。

表1 波速计算参数表Tab.1 Table on parameter for computering wave speed

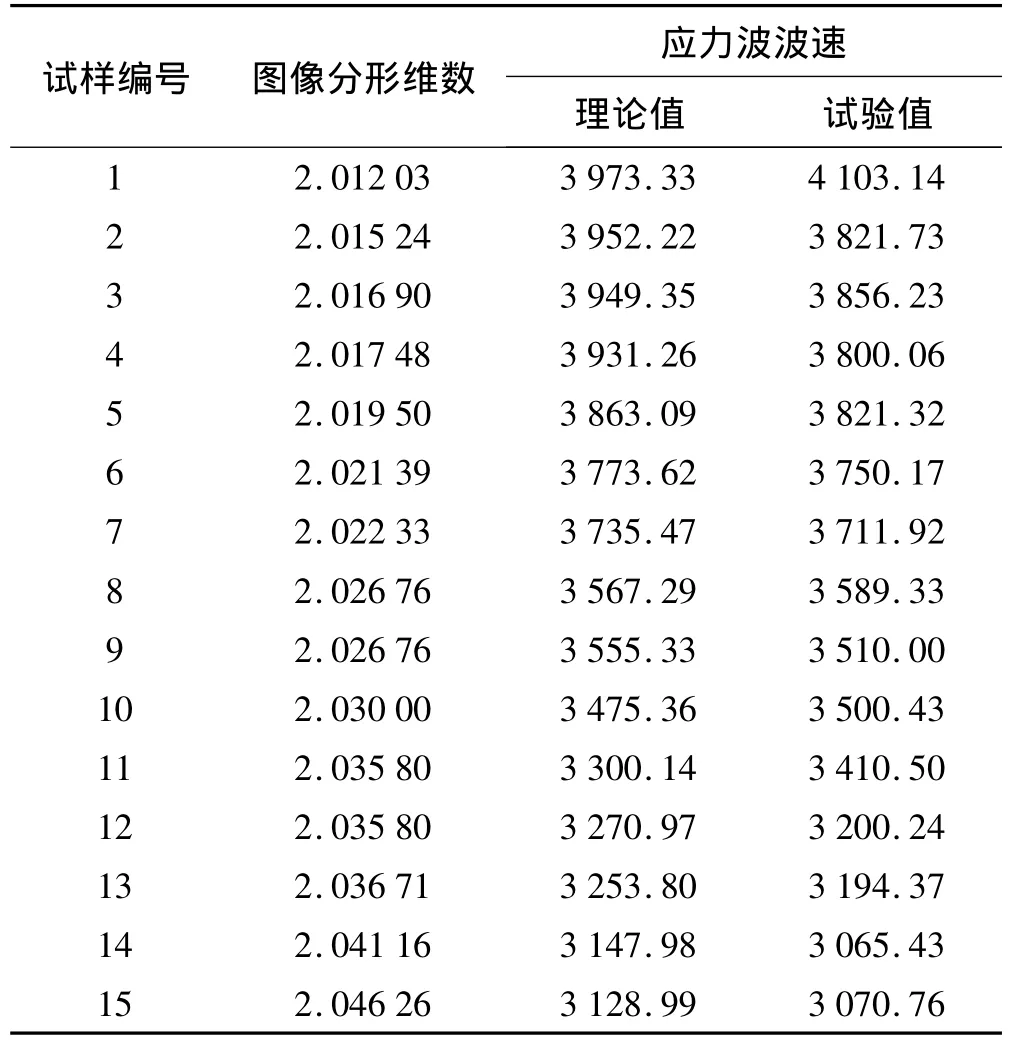
表2 图像分形维数与应力波波速Tab.2 Image dimension and velocity of stress wave

3 节理岩石的超声波试验

为验证节理岩石中波速理论推导正确与否，本节通过节理岩石的超声波试验，测定超声波穿越分形节理的波速，建立波速与图像维数间的关系，并与理论结果进行对比分析。

本试验采用四川大学MTS实验室超声波仪，该设备由超声波信号激发探头，信号接收探头以及显示波形的示波器组成，当超声波信号由激发探头产生后，经岩石介质传至预制节理(见图5)，由于节理与岩石的波阻抗差异，此时超声波将发生复杂的透反射现象，部分反射回发射端，部分超声波穿越节理传至岩样的另一端，被接收探头感知，由示波器采集并保持下来，限于篇幅，本文仅给出了岩样的采集结果(见图6)。分析保存的波形，测量岩样的长度，可分别求取超声波传播的时间与距离，由此计算超声波在节理岩样中的传播速度，计算成果见表2。

图5 超声波仪示意图Fig.5 Schematic figure on ultrasonic apparatus

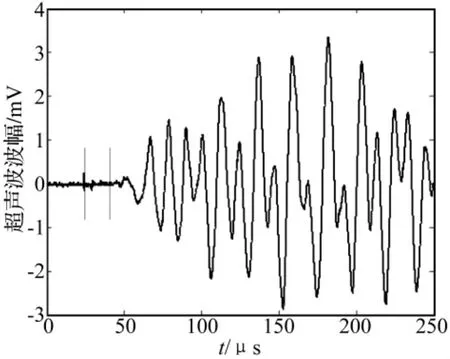
图6 超声波波形Fig.6 Ultrasonic form

4 分析与讨论

依据式(10)计算出的波速(见表2)，我们绘制了波速随维数变化关系曲线图(见图7)，它揭示了应力波穿越不同分形节理时的波速变化规律，并清楚显示:

(1)随着岩石节理面图像分形维数增加，或者说节理面的粗糙度增大，应力波穿越该节理时的波速相应减小。反之，如果节理面图像维数减小，则应力波波速随之增大。两者之间呈现显著的非线性变化关系。这一规律能佐证两点:① 节理面与节理面真彩图像具有一致的分形特性，即:节理面越粗糙，分形维数值越大，则节理面图像从“颜色”角度体现的粗糙度越高，对应的图像分形维数也越大，这与文献［20］的“节理面与其灰度图具有一致的分形性”结论是一致的，所不同的是，本文研究的是真彩图像分形特性，而文献［20］仅探讨了灰度图的分形特性。② 对于两参数间所表现的非线性关系，节理面的不规则性应该“功不可没”，至少可以认为上述规律的出现部分是来自它的“贡献”。

(2)尽管应力波波速随着维数增大持续减小，但波速随维数减小的速率在不同的维数区间里而有所差异。当图像分维在区间［2.01203，2.01690］时，在节理面图像维数增大过程中，应力波波速减小速率相对较小;而当维数大于2.01690且小于2.04116时，应力波波速减小速率加快，约为上一区间的波速变化速率的6.7倍。随着图像维数的进一步增大，当处于区间［2.04116，2.04626］时，波速减小速率反而减缓。

(3)通过与文献［13］的对比分析知，文献［13］与本文得出了类似的研究结论，即:随着节理面粗糙度的增加，应力波波速相应减小。但文献［13］描述节理面粗糙度是文中作者自定义的经验参数——断面粗糙系数(fracture roughness coefficient)，且该文中的结论为探索性的试验成果，而本文通过理论推导得出了应力波在节理岩体中波速的解析解，将描述粗糙性的参数由图像维数取代，克服了文献［13］中的经验主义问题，并将试验研究结论上升到理论高度，是节理岩体中应力波波速研究的一点改进。

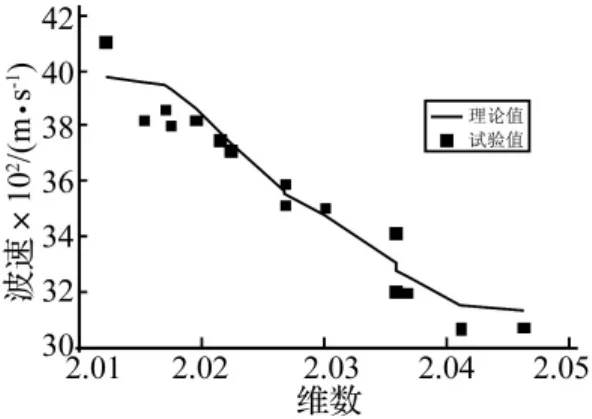
图7 波速与图像维数间的关系曲线图Fig.7 Relation curve between wave velocity and image dimension

5 结论

综合运用分形几何学、图形图像学、损伤力学的相关理论，导出节理面图像维数与应力波波速的解析解，并通过数值方法分析了图像维数改变时穿越节理面应力波波速的变化规律，主要结论包括:

(1)基于真彩图像的像素点颜色可以表示为一个三维空间中矢量的基本假定，构建了节理面图像的“粗糙颜色表面”，依据维数计算原理——立方体覆盖法，计算出该“颜色表面”的分形维数，此维数即为节理面图像的分形维数。并通过实例对该方法进行了验证，结果表明该图像维数计算方法合理可行。

(2)采用分形损伤的基本原理，从构型与参数等效角度推导了应力波在分形节理岩石中传播波速的解析解，从理论上建立了应力波波速与节理面图像维数间的定量关系，即:

(3)通过数值方法，探讨了应力波波速与节理面图像维数之间的相互关系。结果表明:随着节理面图像维数增大，或者说节理面的粗糙度增大，则在节理岩石中传播波速随之减小，两者间呈现非线性变化关系，且在不同的维数区间，波速随维数的变化速率存在差异，上述规律至少能说明两点:① 节理面与其真彩图像具有一致的分形性;② 节理面的不规则性是造成两者间呈现非线性变化关系的重要因素之一。

［1］Gurevich B，Lopatnikov S L.Velocity and attenuation of elastic waves in finely layered porous rocks［J］.Geophysical Journal International，1995，121(3):933 －947.

［2］Wright T W.Elastic wave propagation through a material with voids ［J］. J.Mech.Phys.Solids， 1998，46(10):2033－2047.

［3］邓庆田，杨智春.导波在多损伤板结构中的散射［J］.振动与冲击，2010，29(4):40 －44.

［4］杨宏峰，施行觉.轴向压力下砂岩波速的实验研究［J］.地球物理学进展，2004，19(2):481 －485.

［5］韩 嵩，蔡美峰.节理岩体物理模拟与超声波试验研究［J］.岩石力学与工程学报，2007，26(5):1026－1033.

［6］Oda M.Permeability tensor for discontinuous rock masses［J］.Geotechnique，1985，35(4):483 －495.

［7］Oda M.A crack tensor and its relation to wave velocity anisotropy in jointed rock masses［J］.International Journal of Rock Mechanics and Mining sciences and Geomechanics Abstracts，1986，23(6):387 －397.

［8］胡 刚，郝传波，景海河.爆炸作用下岩石介质应力波传播规律研究［J］.煤炭学报，2001，226(3):270－273.

［9］Ju Y，Sudak L，Xie H P.Study on stress wave propagation in fractured rocks with fractal joint surfaces［J］.International Journal of Solids and Structures，2007，44(13):4256 －4271.

［10］逯静洲，林 皋，王 哲.混凝土经历三向受压荷载历史后强度劣化及超声波探伤方法的研究［J］.工程力学，2002，19(5):52 －57.

［11］刘天云，刘光廷.拱坝地震动随机响应分析［J］.工程力学，2002，17(6):20 －25.

［12］朱金颖，陈龙珠，严细水.混凝土受力状态下超声波传播特性研究［J］.工程力学，1998，15(3):111－117.

［13］Kahraman S.The effects of fracture roughness on P-wave velocity［J］.Engineering Geology，2002，63(3):347 －350.

［14］Mandelbrot B B.How long is the coastline of Britain?Statistical self-similarity and fractal dimension ［J］.Science，1967，155(4):636 －638.

［15］Clarke K C.Computation of the fractal dimension of topographic surfaces using the triangular prism surface area method［J］.Computers ＆ Geoscience，1986，12(5):713－722.

［16］Xie H P，Wang J A.Direct fractal measurement of fracture surfaces［J］.International Journal of Solids and Structures，1999，36(20):3073 －3084.

［17］Zhou H W，Xie H P.Direct estimation of the fractal dimensions of a fracture surface of rock ［J］.Surface Review and Letters，2003，10(5):751 －762.

［18］张亚衡，周宏伟，谢和平.粗糙表面分形维数估算的改进立方体覆盖法［J］.岩石力学与工程学报，2005，24(17):3192－3196.

［19］彭瑞东，谢和平，鞠 杨.二维数字图像分形维数的计算方法［J］.中国矿业大学学报，2004，33(1):19－24.

［20］Pentland A P.Fractal—based description of nature scenes［J］.IEEE Transactions on PAMI，1984，6(6):315 －326.