降低可靠性验证试验用费的分析

胡坤雷

（中国电子科技集团公司第三十八研究所，安徽 合肥 230088）

0 引言

可靠性验证试验是为对产品的设计和生产结果进行检验而进行的试验，包括可靠性鉴定试验和可靠性验收试验两种。可靠性验证试验难度大，投资高，但能获得重要的可靠性信息，是设计生产阶段重要的可靠性管理手段。可靠性验证试验属于工作量大、投资多的可靠性工作项目，目的在于收集可靠性信息，从而作出相应的决策（接受或拒收）。因此，在使用方和订购方经过协商，确定了双方试验风险后， 自然希望选择最经济的、符合要求的试验方案。而目前有关可靠性验证试验降低用费的分析一般还只是定性分析[1]。为此， 本文从定量分析这一要求出发， 对各类可靠性验证试验方案的降低用费方法进行了研究，选取了较为典型的指数寿命型序贯试验方案为研究对象， 建立了降低用费模型，并给出了实用的计算方法。

1 可靠性验证试验及降低用费分析

1.1 可靠性验证试验

可靠性验证试验包括可靠性鉴定试验和可靠性验收试验两种。两者在方法上具有共性，但在试验目的和时机上有差别。可靠性鉴定试验主要是用于检验产品设计和试生产的可靠性指标是否满足可靠性定量要求，而可靠性验收试验则是在生产阶段检验产品的可靠性指标是否仍然满足可靠性定量要求。为了判断待鉴定产品的可靠性是否满足订购方的定量要求，只能随机地选择部分产品（称为样本）进行可靠性验证试验。由于样本具有随机性，虽然样本所代表的可靠性能够反映产品真实的可靠性信息，但却不能恰好地等于产品的真实可靠性。因此，根据样本的结果来作出产品可靠性满足订购方要求（称为接受）或不满足订购方要求（称为拒收）的判断就存在犯错误（即判断错误）的可能性。这种犯错误（即判断错误）的可能性就是决策风险，它分为两类：1）拒收满足可靠性要求的产品，称为犯第一类错误的风险，这是承制方（或生产方） 关心的；2）接受不满足可靠性要求的产品， 称为犯第二类错误的风险，这是订购方（或使用方）关心的。可靠性实验方案一般有全数试验、定时截尾、 定数截尾和序贯截尾试验等几种。其中，截尾试验方案还分无替换和有替换两种。

1.2 降低可靠性验证试验的用费分析

对于定时截尾试验而言，其试验用费的估算比较简单，便于对试验进行计划管理；对于定数截尾试验而言，由于不易估计所需的试验时间及所需的用费，从而在实际中较少应用；在序贯截尾试验中，做出判断所要求的平均故障数和平均累积试验时间与前两种方案相比最小，但其试验时间随着产品的不同而有较大的差别，用费也不易确定。因此，下面以指数寿命型装备的序贯试验方案为例，对如何降低可靠性验证试验用费进行研究。

2 降低指数寿命型序贯试验方案用费的模型

2.1 指数寿命型序贯试验方案

设产品寿命为指数分布，θ为平均寿命。规定：应以高概率接收的合格平均寿命水平为θ0，以高概率拒收的平均寿命下限为θ1，承制方风险为α，使用方风险为β，当产品平均寿命为θ时的接受概率为L（θ），寿命抽样方案应该能够满足以下条件：当 θ=θ0时， L（θ0） =1-α；当 θ= θ1时， L（θ1） =β。

规定：若产品出现故障时相应的总试验时间T相当长，则认为产品合格，予以接收；若相当短，则认为不合格，拒收；若在两者之间，则认为不足以判断，继续试验。于是，判别法则为：在出现r次故障时，看相应的总试验时间 T（r），若：

T（r） ＞ h0+sr， θ=θ0， 产品合格， 接收；

T（r） ＜-h1+sr， θ=θ1， 产品不合格， 拒收；

-h1+sr＜T（r）＜h0+sr，不足以判断，继续试验。

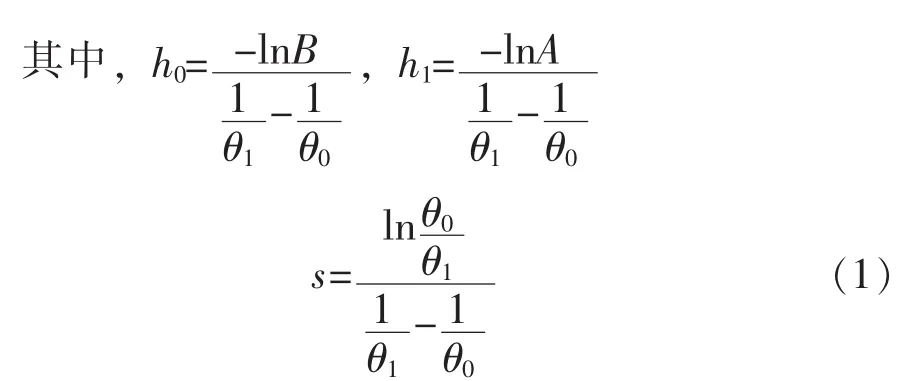
这里的判定数A和B可按下式计算[2]：

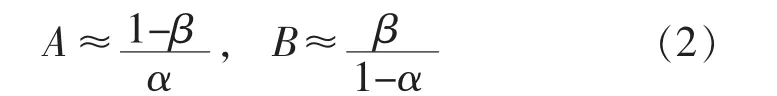
这样，给定α、β、θ0、θ1，序贯寿命抽样方案就完全确定了。

2.2 降低试验用费模型

可靠性验证试验用费可表示如下：

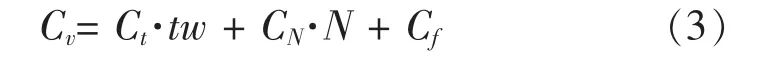
式（3）中：Cv——可靠性验证试验用费；

Ct——单位时间用费；

CN——试验品用费系数；

Cf——试验固定用费；

tw——作出判断前的等待时间；

N——试验品个数。

因为在序贯试验中，tw为随机变量， 故有：

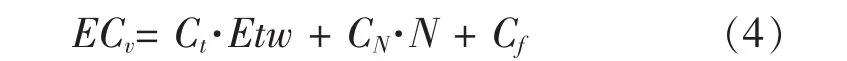
有替换情况下Etw的具体形式为[3]：

式（5）中：Er——在试验中发生的故障数的期望。

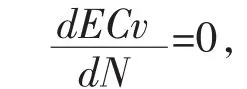
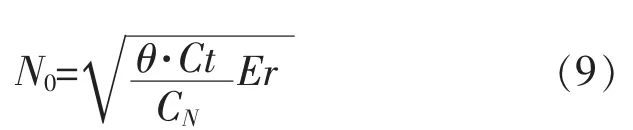
因为N0不一定为整数，所以还需比较N0两端的整数，以确定最优的N*使得Cv最小。

为求N*，必须对试验品的平均寿命进行估计。通常，θ可通过加速寿命测试数据进行推算；模型参数 Ct、CN、Cf可利用历史数据通过最小二乘法拟合；以上模型仅讨论了试验中有替换的情况，无替换的情况在实际中较少应用，且较为复杂，故未进行讨论。方程（7）求解较为复杂，一般需运用数值方法求h的数值解。为使以上模型更为实用，以下选取了多组k，d值计算了对应的值，如表1所示，以方便计算中查阅。

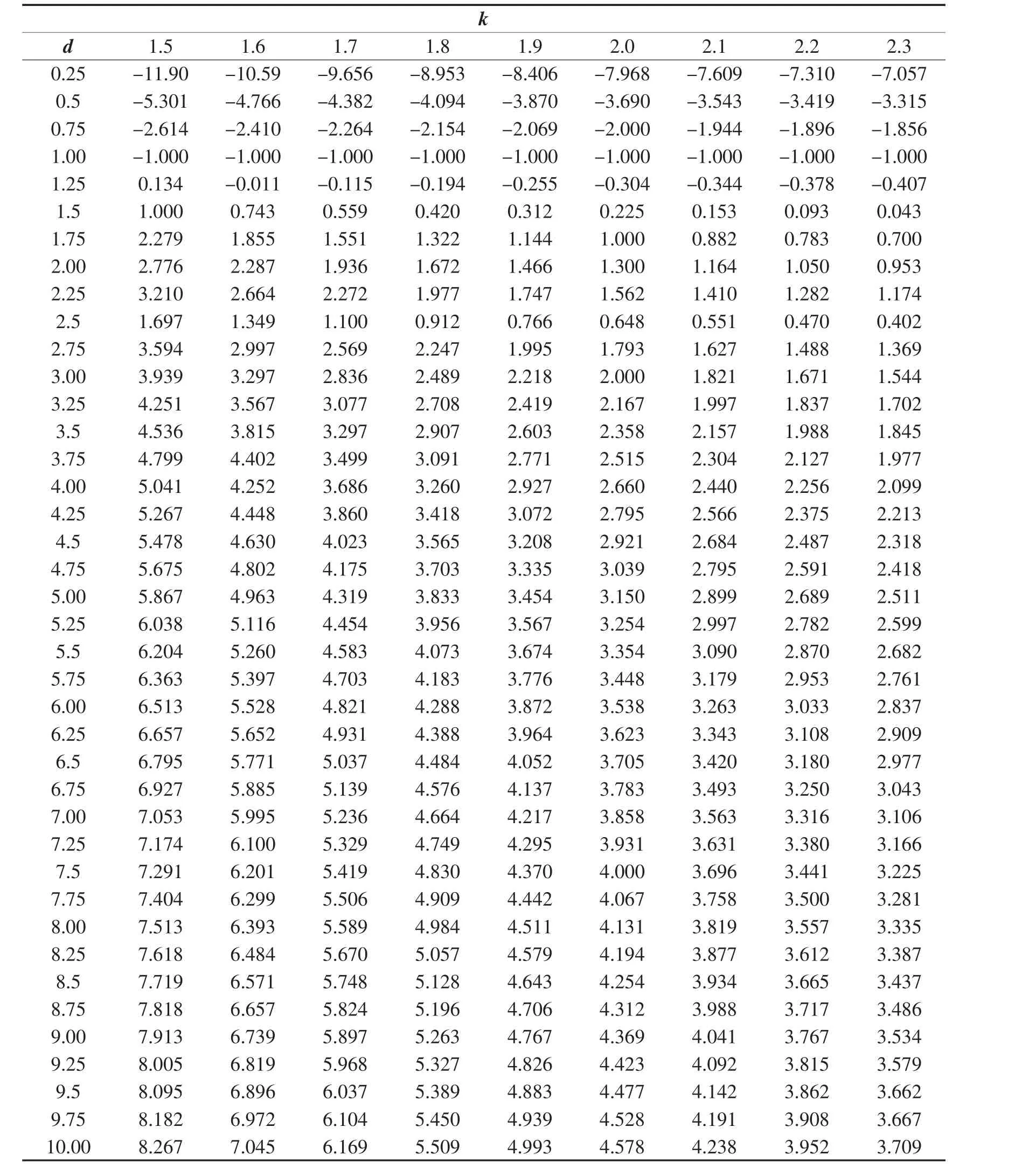
表1 h取值表（k=1.5～2.3）

2.3 计算示例

选取模型的参数如下：

θ0=300h， θ1=450h α=β=0.1， Ct=50元/h，CN=800元，Cf=500元，通过加速寿命试验估算出θ约为 370h，则 k=1.5；d=1.25。查表1得h=0.134。代入模型算得Er=13.27，N0=17.64。比较N0两端整数，最终确定N*=18台。此时，ECv=2.87万元，取得最小值。

从算例看，本文模型及算法具有很好的可操作性和实用性。

3 结束语

本文所建的降低用费模型是针对指数寿命型序贯试验方案的，算例表明了模型及算法的可操作性。对于其它类型的试验方案，有的无需降低，而有的则可参考本文的建模思路予以建模分析，由于篇幅所限，此处不再一一赘述。

[1]GJB 899-1992，可靠性鉴定与验收试验 [S].

[2]黎放，任志久，樊虎.可靠性管理工程 [M].北京：国防工业出版社，1997.

[3]EPSTEIN B，SOBEL M.Sequential life tests in the exponential case[J].The Annals of Mathematical Statistics，1955， 26（1）： 82-93