用计算机做数学作业实践
景德镇高等专科学校 叶艺林
用计算机做数学作业实践
景德镇高等专科学校 叶艺林
文章以应用Mathematica 8做数学作业的形式,介绍了符号计算系统发展前沿的应用状况,期望引起我国数学工作者的重视。一方面尽快在我国的数学教育中充分的反映这些内容,另一方面在数学应用方面,尤其是数学模型技术应用方面,符号计算系统应该像计算器一样走进千家万户。
符号计算系统;计算机代数系统;Mathematica;Maple
一、引言
我们已经步入信息时代,这是一个以计算机技术、网络通信技术、多媒体技术等为核心的信息技术高度应用的时代。可以说当今信息技术已经渗透到人类社会的一切领域,正改变着我们的生活方式和工作方式。掌握信息技术是现代人的基本素质,特别是在科学发展和技术创新前沿,谁掌握了最先进的信息技术谁就能胜出一筹。
我国信息技术发展很快,使用PC机、智能手机、平板电脑等上网交流、获取和发布信息已经是百姓生活的一部分,人们用计算机搜集资料,阅读书、刊、报,写作,创作,设计,制作教学课件等等。不过在辅助学习方面,信息技术应用目前还是有很多地方或方面是处女地,还大有用武之地。比如很少有人用PC机做作业,尤其是用PC机做数学作业。作为抛砖引玉,本文就是想让大家都知道,用计算机也可以做数学作业,而且用计算机做数学作业的操作是非常简单的,期望能够得到普及。
二、符号计算系统简介
符号计算系统或计算机代数系统常指进行符号计算的计算机软件系统。目前流行的符号计算系统很多(参见教材[3]第3页或教材[4]第1页),可分为专用和通用两类。通用符号计算系统,是一个集成化的表示数学知识和数学工具的计算机软件系统,其处理对象从初等数学到高等数学,几乎涉及所有数学学科。Mathematica 8和Maple 15就是两款很好的通用符号计算系统。
Mathematica 8作为一款强大的计算工具,能够支持任意精度的数值计算、符号式运算以及可视化功能,详见网站http://www.wolfram.com/mathematica/features/,本文就选用Mathematica 8这个软件来介绍怎样用计算机做数学作业。
三、用计算机做数学作业实践
1.解析几何作业

图1
例2,求作二次曲线6xy+8y2—12x—26y十11=0的图形。(参见教材[1]第124页例题一)
解:我们只要输入一条指令就可得到所要求作的图形,它是一条双曲线,见图2。
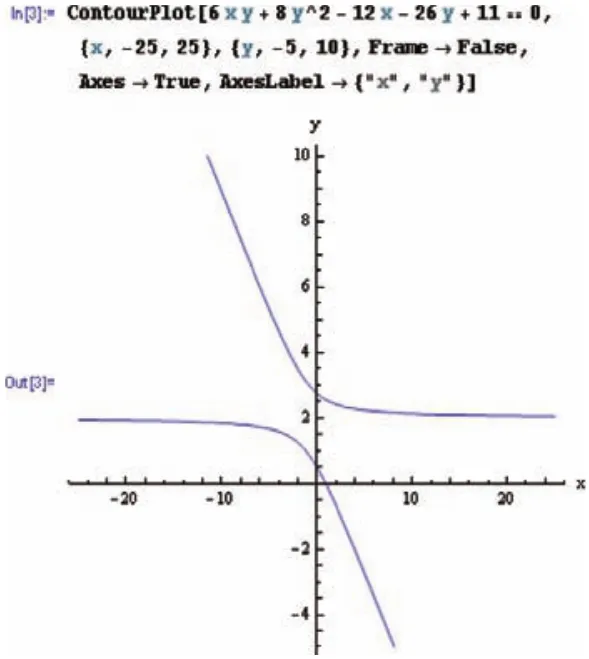
图2
注意:首先这是一个隐函数作图;其次根据图形分布情况,我们可以非常方便地调整图形显示范围,实现最佳作图效果。
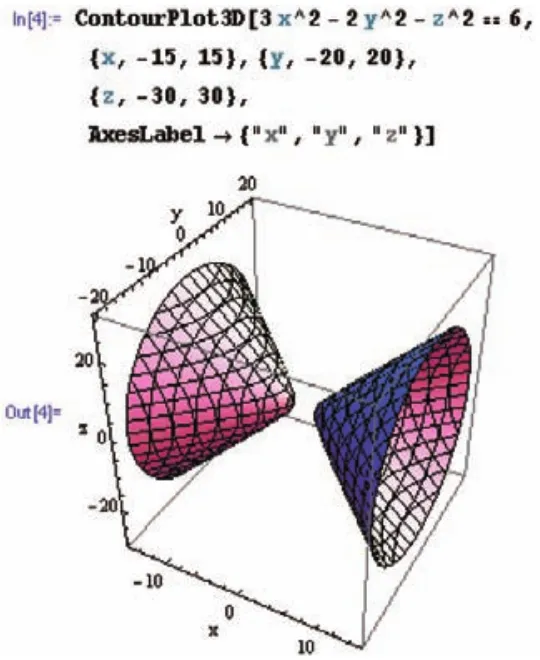
图3
例3:画出曲面3x2-2y2-z2=6的简图:(参见教材[1]第85页第13题的8)小题)
解:输入一条命令即可,见图3,图形是双页双曲面。
例4:求二次曲面S:2xy+2yz+2xz+9=0的标准方程(参见教材[2]第218页例一)
解:首先,把曲面S所对应的系数矩阵赋值给w;再用函数Eigensystem[]获得w的特征值和特征向量;然后用函数Orthogonalixe[]由特征向量组得正交基q;最后验算q.w.qT是一对角矩阵,得该曲面的标准方程为:9x2+2y2-z2=1。具体做法见图4。

图4
2.高等代数作业
例5:设A=(aij)sn,B=(bjk)nm,证明:秩(AB)≧秩(A)+秩(B)-n。参见教材[7]第209页第10题)

图5
证明:只对s=5,n=8,m=6的情形证明,首先,用Table[]函数任意构造一个s×n矩阵和一个n×m矩阵并分别赋值给a,b;然后用MatrixRank[]函数构建要证明的不等式;最后根据计算结果为真,可见命题对s=5,n=8,m=6的情形是正确的。具体做法见图5。
例6:证明:

(参见教材[6]第41备注2)
证明:将等式左边行列式的值赋给c,将等式右边表达式的值赋给d,化简c-d得零。具体做法见图6。
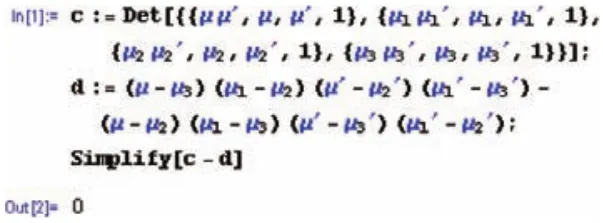
图6
解:首先将矩阵赋值给m;然后用约当分解命令JordanDecomposi-tion[m]得到矩阵s和j,具体做法见图7。

图7

图8
例8:解线性方程组(参见教材[7]第152页第1题1)小题)
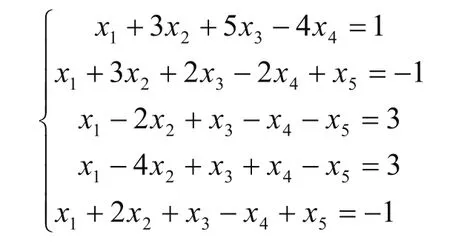
解:将方程组作为Solve[]函数的参数输入,即可得到通解为x1=-t/2,x2=-1-t/2,x3=0,x4=-1-t/2,x5=t。具体做法见图8。
例9:求A-1,

(参见教材[7]第205页第20题6)小题)
解:把矩阵A赋值给a,用Inver-se[a]指令求得
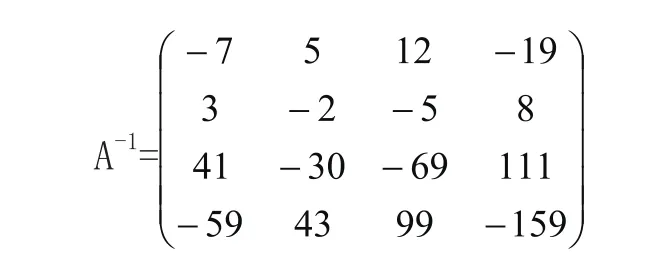
并赋值给b,验证a.b=b.a=I。具体做法见图9。

图9
3.数学分析作业
解:在函数Integrate[]中输入被积函数和积分变量,即得原函数。具体做法见图10。

图10
例11:计算定积分
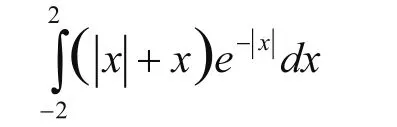
(参见教材[9]第81页例9)
解:只要输入一条命令就得到这个定积分的值为2-6/ã2。具体做法见图11。

图11
(参见教材[9]第19页例18)

图12
解:只要输入一条命令就得到这个极限的值为12。具体做法见图12。
例13:证明:
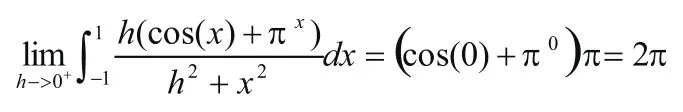
解:只要输入一条命令就得到左边这个极限的值为2π。具体做法见图13。

图13
注意:原题是“假设f(x)在[-1,1]上连续,证明:

(参见教材[5]第211页第6题)例14:设

(参见教材[9]第15页例12)

图14
解:只要输入一条命令就可。具体做法见图14。
例15.求极限

(参见教材[9]第18页例17)
解:只要输入一条命令就可。具体做法见图15。

图15
例16:所谓基本不等式是说:n个非负数的几何平均值不大于算术平均值。即设x1,x2,…,xn是n个非负数,则有

其中等式仅在x1=x2=…=xn时成立。试对n=10验证基本不等式(见教材8第120页13和第121页15题)
证明:我们通过求表达式x1+x2+…+xn在限制条件x1≥0,x2≥0,…,xn≥0,x1x2…xn=1下的最小值来证明:基本不等式的等价形式:x1+x2+…+xn>=n其中x1≥0,x2≥0,…,xn≥0,x1x2…xn=1。具体做法见图16。

图16
四、小结
用计算机做数学作业有如下的特点:
1.作业中的对象必须是具体的。因此,像“假设f(x)在[-1,1]上连续”这样的抽象函数f(x),计算机是不能处理的,计算机只能处理给定的具体函数。尽管如此,由于我们在实际工作中所遇到的数学问题是都是具体的,所以掌握用计算机做数学作业这门技术,对于我们来说依然是十分重要的。
2.用计算机做数学作业的过程一般是人机交互的会话过程,并不需要我们编写程序。我们所要做的只是根据作业题目的内容向计算机发出一条条要求计算机执行计算的指令。也就是说,在用计算机做数学作业的过程中,我们必须要做两件事情:一件是列出做一个具体题目的计算步骤;另一件是根据这些计算步骤依次向计算机发出一条条计算指令,叫计算机去完成每一步具体的计算任务,直到问题得到解决。
3.计算指令一般是以调用函数的形式出现的,并且某条计算指令就是该具体计算的英文名称或者是其缩写。例如,“行列式”的英文名称是Determinant,要计算行列式A,就输入指令Det[A]。不熟悉计算指令的初学者,建议选用Mathemati-ca 8,它有完整的中文帮助。在虚拟全书中,直接输入需要的计算名称就可以查找到需要的计算指令。例如,通过输入“特征值”,可以找到计算“特征值”的指令。
4.虽然计算机的计算能力非常强,但它也不是百分之百的计算都做得出来,而且有的计算结果也会不正确。这一点我们一定要有充分的认识。例如,Mathematica 8不能求出下列级数的极限,见图17。

图17
但是,Maple 15却可以求出这些极限。见图18。
又如,

但是Mathematica 8却会出错,见图19,
可见,不仅不同的计算机代数系统,其计算能力有所不同,而且其计算质量也不差别。上面结果表明Maple 15比Mathematica 8求极限能力要强些,出错也要少些。
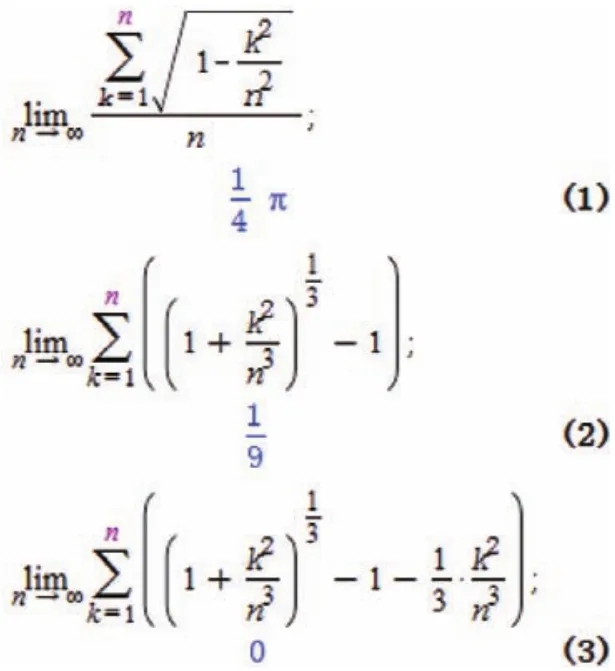
图18
5.由于篇幅所限,以上笔者仅介绍了用计算机做解析几何、高等代数和数学分析三门数学课程的作业,大家千万不要误会,以为用计算机只能够做这三门数学课程的作业。实际上我们用计算机几乎可以做从初等数学到高等数学的全部作业。不过由于数学具有抽象性的特点,而抽象对象计算机又不能处理,因此,对数学作业中大量包含有抽象对象的习题是不能用计算机来做的。例如,我们不能用计算机证明数学分析中的“微分中值定理”。针对这种情况的广泛性,笔者建议大家采用具体的对象代替抽象的对象,再用计算机来处理,以验证这些数学结论。就像上面的例5、例13和例16那样。
[1]吴光磊,田畴.解析几何简明教程[M].北京:高等教育出版社,2003.
[2]宋卫东.解析几何[M].北京:高等教育出版社,2003.
[3]张韵华.符号计算系统Mathematica教程[M].北京:科学出版社,2001.
[4]张韵华,王新茂.符号计算系统Maple教程[M].合肥:中国科学技术大学出版社,2007.
[5]吉林大学数学系.数学分析(上册)[M].北京:人民教育出版社,1979.
[6]朱德祥.高等几何[M].北京:高等教育出版社,1988.
[7]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京:高等教育出版社,1989.
[8]徐利治,王兴华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1983.
[9]郑步南.数学分析典型题选讲[M].桂林:广西师范大学出版社,2003.
叶艺林(1961—),男,江西乐平人,景德镇高等专科学校数学与信息工程系教授,从事教学工作,主编有教材《文献信息检索教程》,发表论文20余篇,研究方向:数学应用。

