具有未知参数的多输入多输出雷达弱目标检测

张海成 杨江平 王晗中

(空军雷达学院，湖北 武汉 430019)

引 言

相比较传统的雷达体制，多输入多输出(MIMO)雷达系统在参数识别和目标检测等方面具有诸多优点[1-5]。现有的MIMO雷达模型通常可以分为两大类：以阵元密布形式来发射和接收信号的基于相控阵体制的MIMO雷达[3]和以大间距的阵元配置以获得空间分集的统计MIMO雷达[4]。统计MIMO雷达可以同时从不同角度观察目标，平滑目标的雷达散射截面 (RCS)起伏，实现发射和接收的空间分集。本文主要讨论后者，采用发射接收都分集的雷达阵列模型。

低信杂噪比环境中对弱目标的检测，已经在信号处理等领域中引起人们的广泛关注。常规的方法主要集中在假设MIMO雷达系统参数已知条件下。对MIMO雷达而言，噪声的统计特性完全先验已知的很少，如果噪声是白高斯噪声，功率可能是未知的，或者噪声是有色但其概率密度函数可能不完全知道。在噪声参数未知的条件下，传统的匹配滤波器输出信号不再形成充分统计量，影响了检测性能，这些非理想的工作条件对MIMO雷达的性能分析、弱目标检测的方法等方面提出了新的要求。

基于上述MIMO雷达设计和实现上的问题，本文结合实际工程研究具有未知噪声参数的MIMO雷达在任意信道环境下的弱目标检测性能分析。讨论了信道完全不相关和信道任意相关下的目标检测性能，给出了任意信道条件下检测概率和虚警概率闭合表达式，通过仿真对分析进行了验证。

1. MIMO雷达建模

考虑一个MIMO雷达系统有M个任意分布的发射天线，有N个任意分布的接收天线。设sk为第k个发射站的基带波形，则第l个接收天线接收到的总信号为[6]

(1)

在接收端采用匹配滤波，匹配后信号表示为

(2)

式中： H0表示τ时刻目标存在； H1表示τ时刻目标不存在；α包含了通道矩阵的所有元素，且服从联合圆复高斯分布，即α～CN(0MN，Rα),Rα=E{ααH}是向量α的相关矩阵，符号H表示共轭转置；n′表示接收端通过匹配滤波后的噪声分量。

2. 新检测器

由于目标信号协方差矩阵不完全已知，假设信道相关矩阵Rα=PCα，弱目标环境下P趋近于0,Cα中元素表征信道之间的相关系数，依赖于具体的目标-阵列结构[7]，有

u)drcosΨrs] ·exp[-j2π(q-

ν)dtcosφts]}

(3)

(4)

式中：R+表示正实数。可以使用局部最大势检验(LMP)，该检测器的优点是只需要计算一个偏导数，检测器可以表示为[8]

(5)

从式(2)，可得H1下概率密度函数为

(6)

将式(6)代入式(5)可得检测器为

(7)

Λa=diag(λα1,…，λαk,…,λαMN)

特征矢量矩阵U=[u1，…，uk，…，uMN]，所以有

(8)

(9)

将式(8)、(9)带入式(6)，并取对数后得到

(10)

(11)

(12)

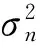
(13)

将式(13)代入式(7)可得

(14)

从式(14)可知，检测器与信道相关系数矩阵Ca有关，实际系统中信道相关矩阵与不同阵列-目标结构有关。

2.1 空间分集下的MIMO雷达目标检测

在空间分集条件下，信道相关系数矩阵Cα是一个单位对角阵，式(14)可以改写为

(15)

则检测统计量的虚警概率和检测概率分别为

(16)

Pd=P(T(x)>δ′|H1)

(17)

2.2 信道部分相关下发射信号能量未知MIMO雷达目标检测

(18)

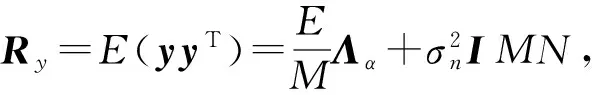
(19)

式中：

则相应虚警概率为

Pf=p(T>δ′|H0)

(20)

同理，目标检测概率为

Pd=p(T>δ′|H1)

(21)

3．数值仿真

在理论推导的基础上，通过计算机仿真模拟了MIMO雷达检测器的性能，分析了具有任意阵列—目标结构的MIMO雷达在未知噪声方差情况下对目标检测性能的影响。假设发射天线M=2，接收天线N=4，目标是由1 000个服从圆复高斯分布的散射点构成，发射载频为1 GHz，发射阵元、接收阵元间距均为600 m.
图1表示不同信道情况下的漏检概率(Pmd=1-Pd)，从图1可以看出，具有未知参数的MIMO雷达检测性能以统计MIMO雷达的性能为上限，并且信道矩阵的相关性会引起检测性能损失。图2表示不同信道情况下的漏检概率。信噪比相同时，噪声参数未知的非相关信道下MIMO雷达漏检概率最高，模拟结果与理论结果相符，从而进一步确认了检测器算法的有效性。

图1 MIMO雷达虚警概率和漏警概率的关系

图2 MIMO雷达漏检概率与信噪比的关系

4. 结 论

针对MIMO雷达在未知噪声方差下的弱目标检测问题，提出了从空间分集情况下到信道部分相关下的MIMO雷达检测器，给出了任意信道环境下的检测性能解析表达式，通过数值试验验证了方法的有效性，因而该方法更大程度地满足了工程设计的需要。

[1] FISHLER E, HAIMOVICH A, BLUM R, et al. MIMO radar: an idea whose time has come[C]//Proceeding of Conference on Radar. Philadelphia, USA, 26-29 April, 2004: 71-78.

[2] FISHLER E, HAIMOVICH A, BLUM R, et al. Performance of MIMO radar systems: advantages of angular diversity[C]// Proceeding of Conference on Signals, Systems and Computers. Pacific Grove, CA, 7-10 November., 2004:305-309.

[3] LI J, STOICA P. MIMO radar with collocated antennas [J]. IEEE Signal Process, 2007, 24(5): 106-114.

[4] HAIMOVICH A M, BLUM R S, CIMINI L J. MIMO radar with widely separated antennas [J]. IEEE Signal Processing, 2008, 25(1): 116-129.

[5] HAIMOVICH A, BLUM R, CIMINI LJ. MIMO radar with widely separated antennas[J]. IEEE Signal Processing, 2008, 25 (1):116-129.

[6] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars models and detection performance [J]. IEEE Trans Signal Processing, 2006, 54(3): 823-838.

[7] PETILLOT Y, DU C R, THOMPSON J S. Predicted detection performance of MIMO radar[J]. IEEE Signal Processing Letters, 2008, 15: 83-86.

[8] KAY S M. Fundamentals of Statistical Signal Processing: Detection Theory[M]. London: Prentice Hall Professional Technical Press, 1993.

[9] PROAKIS J G. Digital Communications [M]. BostonMC Graw-Hill, 1993.

[9]Proakis J G. Digital Communications. Boston: MCGraw-Hill, 2001.