基于人工神经网络的负荷算法的优化
张嘉嘉
(中国石化工程建设公司,北京 100101)
电力系统负荷预测是根据电力负荷、经济、社会、气象等的历史数据,探索电力负荷历史数据变化规律对未来负荷的影响,寻求电力负荷与相关因素之间的内在联系,从而对未来的电力负荷进行科学的预测[1],为电力系统规划和运行提供可靠的依据[2]。
论文介绍了人工神经网络预测方法,并对日负荷数据进行程序仿真。在此基础上,论文对人工神经网络中BP 算法进行了改进,建立了组合预测神经网络模型,使用了Matlab 中的cftool 工具箱对日负荷数据进行仿真,结果表明改进的组合预测神经网络模型具有更好的精度和应用价值。
1 人工神经网络结构
人工神经网络中一个重要部分就是单元联接形式,也就是网络的结构形式。神经网络的命名往往根据他的结构特点,或者根据采用的学习方法(简称算法)。目前常用的网络结构形式如下。
1)分层网络(又称前向多层网络,前馈网络等)
分层网络是指网络中具有相同拓扑结构地位的神经元构成的一个子集;它是作为有向图的人工神经网络图中处于同一列或同一行上的节点;它们是运算处理程序进行过程中的同一个段面;它所属的每一神经元的权向量参与构成一个独立的权矩阵。如果网络中有多个这样的人工神经元子集,就构成了一种多层网络。多层网络信息的前向传递处理过程是一个输入特征向量从高维空间逐次映射的过程,是一个输入向量按特征聚类的过程;是与生物系统的由感觉器官对外部世界事务特征的摄取知道认知完成这样一个高度抽象的过程的过程完全类似的,是一件具有深邃含义事物的模型和数学的表征。
前馈网络的基本要素是能用一个前向无环路有向图表示,如图1所示。
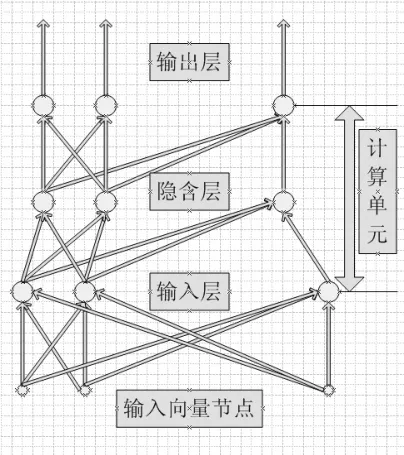
图1 前向多层网络示意
就是说,必须不存在前层神经元输出y 向后层传递的支路;更不允许一个神经元的输出向其自身输入端传送的支路,否则严重违反生物神经元单向传递特性;严格的讲存在同一层神经元输出向本层其他神经元的输入端传递支路的网络,也不应属于前向多层网络。
2)互联网络(或称反馈网络)
典型的反馈型网络如图2所示。
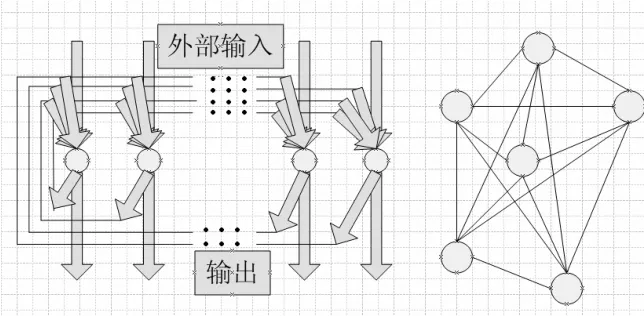
图2 互联网络模型

图3 BP 神经网络
图2中每个节点都表示一个计算单元,同时接受外加输入和其他各节点的反馈输入,每个节点也都直接向外部输出。Hopfield 网络即属于此种类型。在某些反馈网络中,各神经元除接受外加输入与其他各节点反馈输入之外,还包括自环反馈。
3)BP 网络结构
图3是具有一个隐含层的BP(Back-Propagation)神经网络模型结构图(图中输入节点j=1,2,…,r;隐含节点i=1,2,…,s1;输出节点k=1,2,…,s2),其输入层神经元数为r,隐含层神经元数为s1,输出层神经元数为s2,隐含层神经元的激活函数为,输出层神经元的激活函数为F2,输入为P,输出为A。如果不计输入层,就可称其为两层神经网络。
2 改进的神经网络负荷预测方法
尽管BP 算法在实际工程中得到了广泛应用,但也存在着自身的局限和不足,主要表现在收敛速度慢、局部极小值、训练瘫痪等问题。针对BP 算法的缺点,提出以下几种改进方法。
1)动量法
该方法是在反向传播法的基础上,对每一个全职的变化再加上一项正比于前次权值变化量的值,并根据反向传播法产生新的权值变化。带有动量因子的权值调节公式为
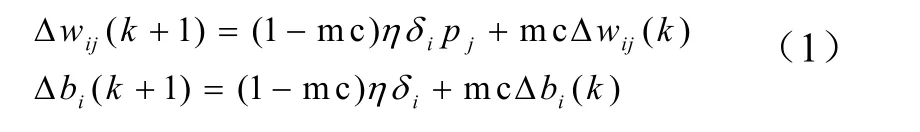
式中,k为训练次数;mc 为动量因子,一般取0.95左右。
2)自适应调整学习速率算法
对于一个特定的问题要选择适当的学习速率不是一件容易的事。学习速率选的太小,收敛太慢;选的太大,特有可能修正过头,导致振荡甚至发散。为了解决这一问题,可以再训练过程中自动调整学习速率。学习速率η的自适应调整公式为

式中,SSE 为误差平方和。
3)动量-自适应调整学习速率算法
当采用动量法时,BP 算法可以找到更优的解;而采用自适应调整学习速率法时,BP 算法可以缩短训练时间。综合采用以上两种算法,不仅可以避免网络陷入局部极小值,而且还能加速网络收敛。
4)利用Levenberg-Marquardt 学习规则
更新权值参数的L-M(Levenberg -Marquardt)学习规则为

式中,e为误差矢量;J为网络误差对权值导数的雅可比(Jacobian)矩阵;I为单位矩阵;μ为一个标量,其大小决定了算法是根据牛顿法还是梯度法完成。
Levenberg-Marquardt 优化算法比前述几种使用梯度下降法的BP 算法快很多,但它需要更多的内存。
5)电力负荷组合预测[3]
组合预测方法是对同一个预测问题,将多个不同的预测模型有机地组合在一起,综合各模型的优点,以期有效地改善模型的拟合能力,提高预测精度。加权处理是一种常见的处理手段,基本思想是:在某一预测问题中,在某一时段的实际值为yt(t= 1,2,···,n)。对该问题有m种预测方法,其中利用第i种方法对t时段的预测值为f it(i= 1,2,···,m)。如果各种预测方法 的权重为W= [w1,w2,···,wm]T,满足组合预 测模型可表示为

式中,w因子可用拉格朗日乘数法或其他数学规划方法确定。
上述组合预测方法,只对权重进行线性组合,要求参加组合预测方法的误差能保持稳定,但电力系统负荷预测结果的误差往往是非均匀性的,因而这种组合校正可就存在不足。考虑到人工神经网络对复杂线性的拟合能力,构造了基于人工神经网络的组合预测模型。
采用人工神经网络进行组合预测的模型如图4所示。
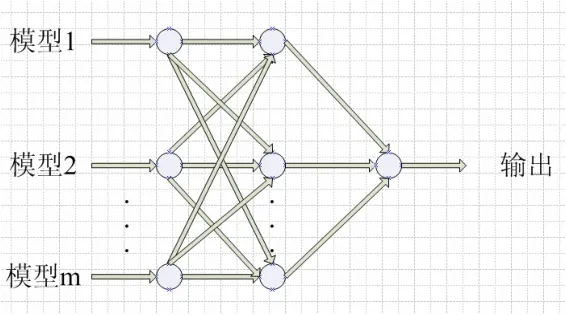
图4 组合预测神经网络模型
其中模型1、模型2,…,模型m为不同的单个预测模型。输入层神经元个数m为不同的单个预测模型数,输入层为一个神经元,即得到一个组合输出,隐层个数可经试验确定。
选择与预测量最近的n个已知值作为样本,即把最近的n个已知值作为输出,采用不同的单个预测模型对这n个已知值分别进行预测,其预测值即为神经网络的输入,由此对神经网络进行训练。对于训练好的神经那个网络,当输入端为不同的单个模型预测值时,其输出即为用神经网络组合后的预测值。
3 Matlab 算例仿真
对文献[4]某城市的2004年7月10-7月20日的整点有功负荷值进行仿真计算。数据见表1和表2。
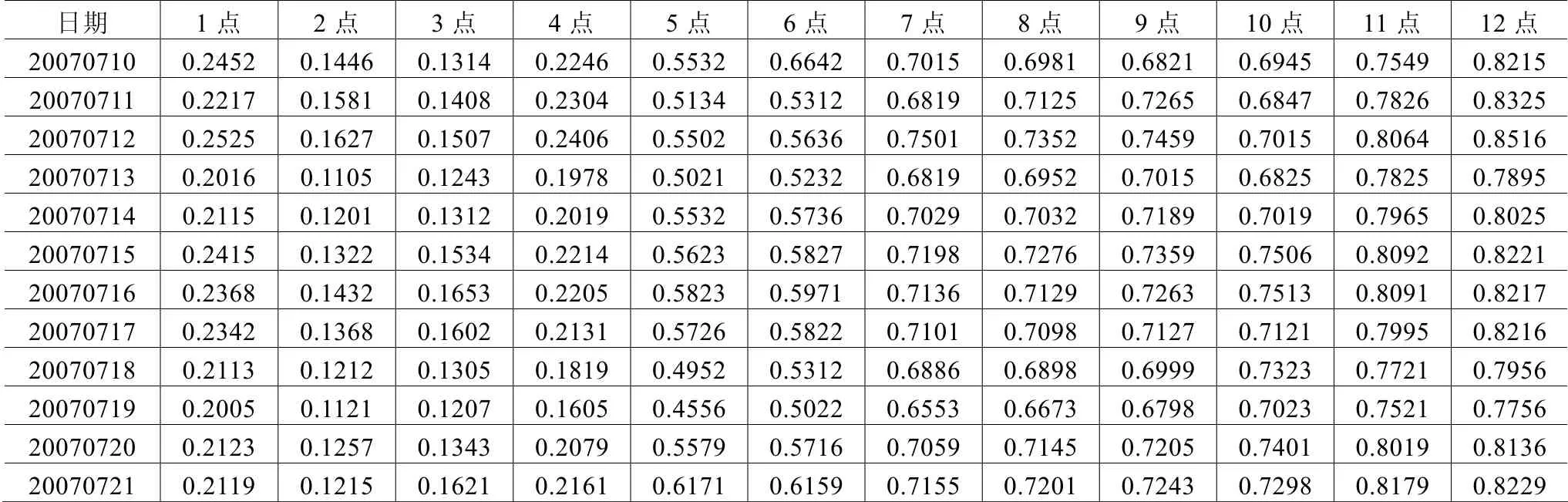
表1 某城市7月10-20日的整点有功负荷值
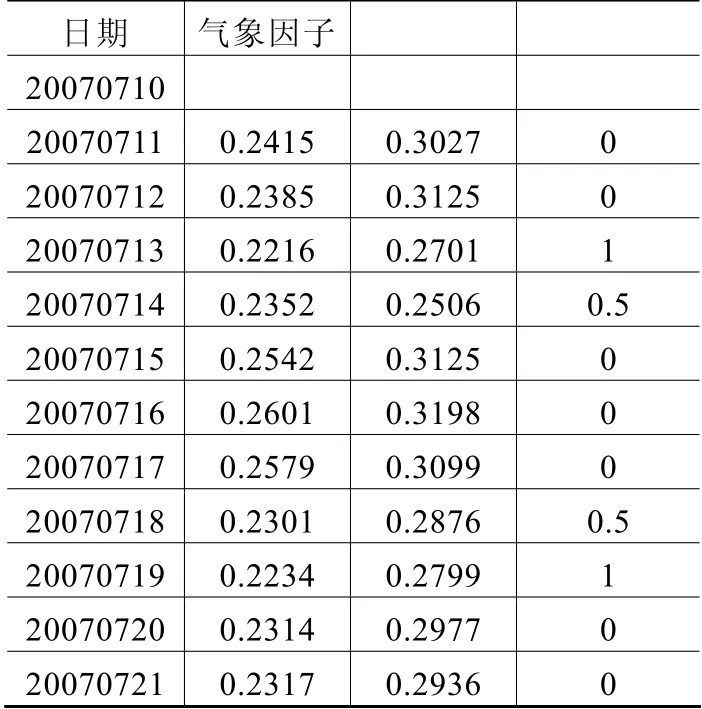
表2 某城市7月10-20日的气象因子数值
1)梯度下降BP 算法函数算例结果
采用梯度下降BP 算法对表1和表2的数据进行仿真,结果如图5和表3所示。
预测结果输出见表3。

图5 梯度下降BP 算法训练结果

图6 梯度下降动量BP 算法训练结果
2)基于梯度下降动量BP 算法
改进算法1 是基于动量-自适应调整学习速率算法进行训练的人工神经网络模型。其中网络结构为3 层BP 网络,输入层神经元的个数为15,输出层神经元的个数为12,隐含层神经元个数取为31,隐含层神经元的传递函数采用tansig,输出层神经元的传递函数采用 purelin。网络训练函数采用traingdm,相应的学习函数为learngdm 具体训练参数是:动量因子为0.98,学习速率为0.2,训练指标误差为0.0001,最大训练步数为5000,每25 步显示一次。计算结果如图6和表4所示。
3)基于L-M 学习规则进行训练的人工神经网络模型的仿真
基于L-M 学习规则进行网络训练,其中训练函数函数选用TRAΙNLM。具体的训练参数为:网络训练函数采用trainlm,相应的学习函数为learndm,学习速率为0.1,训练指标误差为0,最大训练步数为1000,每25 步显示一次。其结果与实际值比较如图7所示。经计算,利用此方法预测数据的均方差达到6.2814e-004。
4)3 种算法预测结果比较
以下对上述3 种人工神经网络预测方法进行对比。3 种方法的预测结果如图8所示,误差见表5。
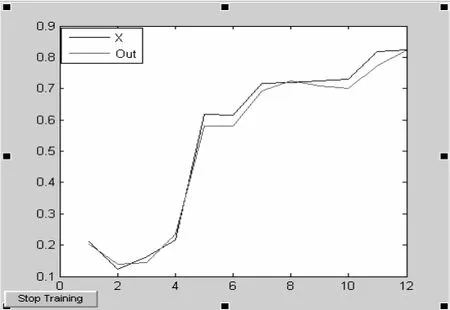
图7 利用L-M 方法输出的结果与实际值比较 (X 为实际值,Out 为预测值)

图8 神经网络3 种方法预测值曲线图比较

表3 梯度下降BP 法输出值与实际值误差比较

表4 梯度下降动量BP 法输出值与实际值误差比较

表5 梯度下降BP 算法与两种改进方法应用于日负荷预测的误差值比较
由图8可以表明,改进的算法进行预测的结果优于没有改进的方法,且在日负荷预测中,人工神经网络具有很明显的优势。
4 结论
对于变化快时间短的日负荷预测,人工神经网络方法能够依靠其人工神经网络的训练得到更加适合的算法。在神经网络的方法中,通过选取不同的训练函数,可以实现不同模型组合的非线性拟合,同时也提高了电力负荷预测的精度。利用Matlab 神经网络工具箱编程,使网络训练程序比用其他语言编制的效率更高,训练时间更短。算例结果表明基于Matlab 神经网络工具箱的电力负荷组合预测模型简洁、实用,并且具有较高精度。
[1] 康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007:4-22.
[2] 程浩忠.电力系统规划[M].北京:中国电力出版社,2008:13-16.
[3] 刘双,杨丽徙,王志刚,等.基于Matlab 神经网络工具箱的电力负荷组合预测模型[J].电力自动化设备,2003,23(3):59-61.
[4] 张德丰.Matlab 神经网络应用设计[M].北京:机械工业出版社.2009:215-217.

