非定常人工通气超空泡数学仿真与分析

王改娣, 吕艳慧, 邹启明



非定常人工通气超空泡数学仿真与分析

王改娣, 吕艳慧, 邹启明

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710075)

针对人工通气超空泡涉及因素多、时变特性强、实现难度大、成本代价高的复杂工程问题, 开展了非定常人工通气超空泡数学仿真研究。根据Logvinovich的空泡截面扩展独立性原理, 建立了非定常通气超空泡形态模型,给出了仿真计算方法, 对影响超空泡形态的因素进行了动态仿真计算, 得到了不同充气参数和运动参数下空泡形态变化规律以及与航行体表面的相对位置关系, 提出了满足航行体高速运动稳定的空泡闭合位置要求。研究结果对水下高速航行体的通气系统设计和航行性能设计均具有重要的参考价值, 并可为工程应用研究提供理论基础。

水下高速航行体; 非定常; 通气超空泡; 数学仿真

1 概述

当水下运动的航行体与液体相对高速运动时, 航行体表面附近的液体因低压而发生相变, 形成薄的包含水汽的包层, 即空泡。以这种方式形成的空泡长度与航行体长度相当或将航行体包裹时, 便称为自然超空泡或蒸汽超空泡。受水下航行体速度限制和其他干扰影响, 自然超空泡难以维持较长时间。然而, 以自然超空泡流场为依托, 通过向空泡内注入气体, 可生成覆盖物体部分或全部表面的内部主要含有气体的超空泡, 这便是人工通气超空泡[1]。利用超空泡产生的原理和特性来设计的航行体, 在水下运动过程中可生成大小、长度、闭合位置等满足航行体稳定运动要求的超空泡[2], 使航行体表面的大部分与水隔开, 减小了与水之间的粘性摩擦损失, 从而大大减小航行阻力, 获得难以想象的水中高速。

一般情况下, 随着航行体速度增加和通气量调整, 超空泡的发展经历了从局部空泡到超空泡, 从自然超空泡到通气超空泡, 从非定常超空泡到定常超空泡等过程。实际上, 这一过程中的人工通气超空泡是一个涉及因素很多、时变特性很强、实现困难很大、成本很高的复杂工程问题, 而通气超空泡的生成和稳定对航行体运动会产生重大影响。

针对工程上难以实现的人工通气超空泡问题, 国内外已有大量的研究[3-6], 但目前还少有通气超空泡与航行体运动关系方面的研究报道。本文考虑了航行体的运动特性, 分析了非定常通气超空泡发展过程及特点, 建立了数学仿真模型, 提出了仿真方法, 对不同影响因素下的超空泡形成过程进行了动态数学仿真, 得到了空泡形态变化规律以及与航行体表面的相对位置关系, 以便为人工通气超空泡的工程应用研究和高速水下航行体运动稳定性研究提供理论参考。

2 非定常通气超空泡发展过程及特点

外形设计满足超空泡生成条件的水下航行体, 随着运动速度的增大, 在航行体表面生成了由局部空泡发展的自然超空泡, 由航行体头部通气孔向自然超空泡内射入气体, 在来流作用下贴着壁面向下游发展, 形成覆盖航行体表面充满气体的气囊, 即通气超空泡。利用自然超空泡具有向其内部充气形成更大超空泡的这一特点, 产生具有相对稳定、大小可控、形态满足要求的通气超空泡。

通气超空泡的形成一般是在航行体定深后的加速过程中即速度场变化中, 而为了快速形成超空泡, 要求通气量与速度相匹配, 即先大后小, 最终趋于稳定, 这就使得空泡内部充气压力发生变化, 即航行体表面压力场变化。可以看出, 通气超空泡是在非定常流场中形成的, 这种内外压力和沿自由边界速度都随时间变化的超空泡为非定常超空泡。

非定常通气超空泡具有以下几个特点: 1) 超空泡流场具有非定常、可压缩、相变、湍动等复杂特性; 2) 超空泡外形具有一定的形状和大小; 3) 沿超空泡长度上具有平滑、清晰的边界; 4) 在通气量控制下, 空泡形态具有一定的稳定性和可控性; 5) 超空泡形状受重力场和航行体运动参数影响后会发生变形, 即相对于航行体不对称等。利用上述特点, 在航行体运动过程中, 可生成大小、形状、长度、闭合位置等满足航行体受力平衡和运动稳定要求的超空泡。

本文暂不考虑流场特性对空泡的影响, 主要研究通气系统的充气参数和航行体的运动参数对空泡形状的影响。

3 非定常通气超空泡数学模型

非定常轴对称超空泡模型是建立在G.V. Logvinovich的所谓细长轴对称空泡截面扩展独立性原理上[7-8], 该原理的要点是, 空泡截面扩展规律由通过该截面平面时空化器瞬时速度以及压力差所确定, 其形状如图1所示。

图1 非定常轴对称超空泡

根据该原理, 空泡截面扩张方程为

其中

方程(1)的积分初始条件为

考虑到重力场和航行体运动参数的影响, 超空泡轴线会发生一定的偏移, 为方便研究, 本文建立了从航行体头部空化器中心开始沿着航行体纵轴方向的偏移量表达形式, 即

4 非定常通气超空泡仿真方法

对非定常人工通气超空泡进行数学仿真, 是为了研究通气空泡形成过程中, 空泡形态的变化特性以及与航行体表面的相对位置关系, 从而得到满足空泡稳定和航行体运动稳定的通气参数和运动参数, 仿真计算方法如下。

1) 数学模拟航行体结构外形

航行体结构外形与空泡形成过程及闭合位置密切相关, 尤其是头部空化器的形状, 空化器除了生成超空泡流场外, 还起到水平舵的作用, 舵角大小对空泡变形有一定影响。

2) 设置仿真初始条件

非定常超空泡的仿真初始条件包括初始泡内压力、初始空泡数、初始速度和初始航深等。

3) 选择通气规律

人工通气超空泡的通气量根据航行体的速度变化和弹道要求确定, 在仿真开始前预设定通气规律, 仿真计算中按照一定的时序执行。

4) 空泡形态仿真计算

5 不同影响因素下的仿真结果及分析

本文以俄罗斯“暴风雪”超空泡鱼雷为背景, 设计了水下高速航行体结构外形, 并设定仿真条件如下。

初始条件:P0= 2 350 Pa,0=70 m/s;

弹道形式: 定深直航。

充气规律和速度变化规律如图2所示。

图2 充气规律和速度变化规律

5.1 充气参数影响

本节主要研究速度加速过程中空泡形成过程的变化规律, 得出充气过程与加速过程的匹配关系, 以便确定满足充气稳定和航行体运动稳定要求的充气参数。

1) 充气率大小影响

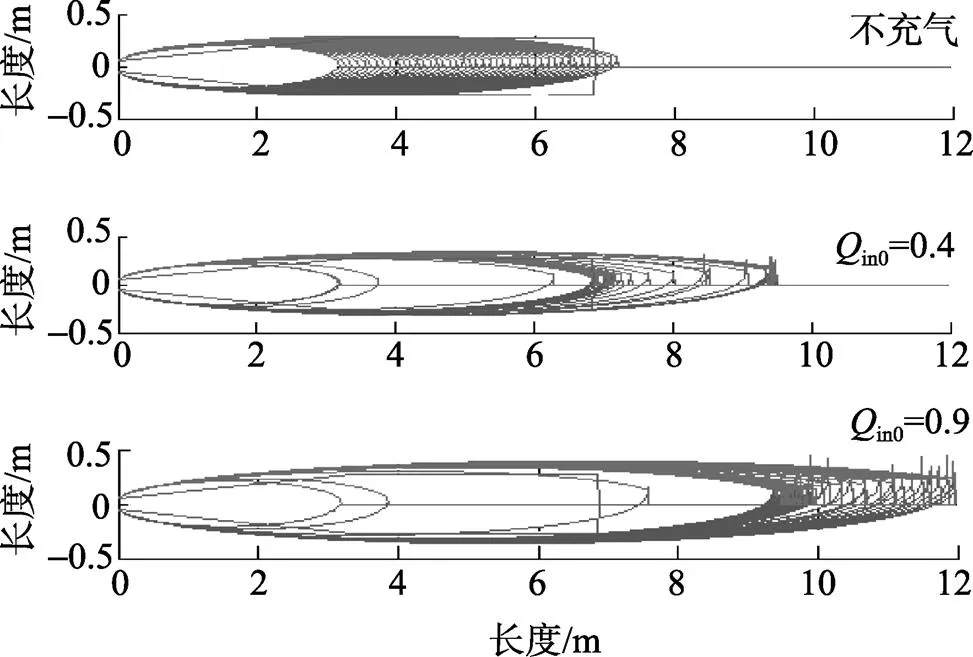
图3 不同充气率下的空泡形成过程变化曲线

从图3可以看出, 如果不充气, 随着速度的增大,在航行体表面形成的自然超空泡均匀增大, 虽然稳定时能够闭合在雷体表面, 但是闭合位置不满足航行体带空泡稳定航行的要求。人工充气后, 空泡迅速拉长增大, 随着充气率增大, 超空泡长度拉长, 闭合位置向后移动, 直至变为开式超空泡。

2) 加速充气系数影响

当其他充气参数一定时, 不同加速充气系数下空泡形状变化的仿真曲线如图4所示。

图4 不同充气系数下的空泡形成过程变化曲线

从图4看出, 加速充气系数对通气超空泡形成过程中的空泡形态有显著影响, 系数越大, 加速充气过程生成的最大空泡尺寸越大, 继续增大, 由最大充气率生成的空泡将由闭式变为开式, 但对稳定后的超空泡没有多大影响。根据这一变化规律, 就可以针对不同航行体确定出最佳的充气系数, 使得加速过程中所形成的通气超空泡也能满足航行体运动稳定的闭合位置要求。

5.2 运动参数影响

在5.1节基础上, 进行航行体运动参数对空泡形状影响的仿真, 其目的是研究在充气稳定和速度稳定条件下空泡变形的规律, 找出维持航行体运动稳定要求的空泡闭合位置, 以便对运动参数变化范围提出要求。

1) 来流攻角影响

图5是不同来流攻角下, 超空泡形成过程中的仿真结果。

图5 不同攻角α下超空泡形成过程变化曲线

从图5可以看出, 来流攻角会引起超空泡变形, 使超空泡相对于航行体变得不对称, 即空泡向上偏移。空泡变形后, 航行体上下表面的闭合点位置将不对称, 下闭合点前于上闭合点。攻角存在时, 随着攻角增大, 空泡向上偏移量增大, 使得下闭合点位置前移, 上闭合点逐渐变为开式。当攻角增大到一定程度时, 空泡严重变形, 实际中会溃灭, 满足不了航行体高速稳定运动的要求, 容易造成运动失稳。

2) 空化器舵角影响

当作为前置舵的空化器有舵角存在时, 也会使超空泡发生变形, 在此选择来流攻角=0°, 通过设置不同的空化器舵角δ, 由仿真计算得到超空泡形成过程中相对于航行体变形的仿真结果, 如图6所示。

图6 不同舵角δn下超空泡形成过程变化曲线

由图6可以看出, 在攻角为0前提下, 当空化器前倾一舵角时, 会使空泡相对于航行体变得不对称, 即空泡向下偏移。随着舵角增大, 下闭合点逐渐后移, 上闭合点逐渐前移, 二者之间的位置差逐渐增大。空化器舵角增大到一定值时, 空泡上闭合点位置前移也会造成空泡溃灭和航行体运动失稳。

在实际运动过程中, 航行体的攻角不可能为0, 由攻角产生的空泡上偏移会部分抵消由空化器舵角产生的下偏移, 从而满足航行体运动稳定对空泡闭合位置的要求。

6 结论

针对人工通气超空泡工程上难以实现的问题, 开展了对非定常人工通气超空泡的生成过程和形态变化的数学仿真研究, 建立了通气超空泡数学模型, 提出了仿真计算方法, 对影响超空泡形态的主要因素即充气参数和运动参数进行了仿真计算, 得到了如下结论。

1) 水下高速运动航行体只有通过人工通气的方式, 才能生成满足航行体运动稳定要求的超空泡;

2) 充气参数对通气超空泡生成过程的形状和大小以及在航行体表面的闭合位置影响很大, 需要针对航行体结构外形和弹道需求来确定充气参数;

3) 航行体运动参数对空泡变形影响较大, 即正攻角使空泡产生上偏移, 空化器舵前倾使空泡产生下偏移, 二者匹配关系要满足航行体在空泡包裹下稳定运动时对空泡闭合位置的要求。

[1] Semenenko V N. Artificial Supercavitation Physics and Calculation[C]//VKI Special Course on Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001.

[2] Savchenko Y N. Control of Supercavitation Flow and Stability of Supercavitating Motion of Bodies[C]//VKI Special Course on Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001.

[3] Semenenko V N. Dynamic Processes of Supercavitation and Computer Simulation[C]//VKI Special Course on Super-ca- vitating Flows. Brussels: RTO-AVT and VKI, 2001.

[4] 蒋运华, 安伟光, 安海, 超空泡运动体通气加速阶段非定常过程研究[J]. 弹道学报, 2011, 23(2): 67-71. Jiang Yun-hua, An Wei-guang, An Hai. Study on Unsteady Process of Ventilation Accelerated Motion Stage for Supercavitating Vehicle[J]. Journal of Ballistics, 2011, 23(2): 67- 71.

[5] 张学伟, 魏英杰, 张庆丽, 等. 通气空泡发展过程及其水动力影响[J]. 哈尔滨工业大学学报, 2008, 40(7): 1031- 1035, 1054. Zhang Xue-wei, Wei Ying-jie, Zhang Qing-li, et al. Development of Ventilated Cavitation and Its Effect on Hydrodynamics[J]. Journal of Harbin Institute of Technology, 2008, 40(7): 1031-1035, 1054.

[6] 陈鑫, 鲁传敬, 吴磊. 通气超空泡的形态特性研究[J]. 弹道学报, 2005, 17(1):1-7. Chen Xin Lu Chuan-jing, Wu Lei. The Investigation on Morphology of Ventilated Supercavity[J]. Journal of Ballistics, 2005, 17(1):1-7.

[7] Vasin A D. The Principle of Independence of the Cavity Sections Expansion (Logvinovich′s Principle) as the Basis for Investigation on Cavitation Flows[C]//VKI Special Course on Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001.

[8] Paryshev E V. Mathematical Modeling of Unsteady Cavity Flows[C]//5th International Symposium on Cavitation, Osa- ka, Japan, 2003.

Mathematical Simulation of Unsteady Ventilated Supercavitation

WANG Gai-di, LÜ Yan-hui, ZOU Qi-ming

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

Considering the complex factors concerned in ventilated supercavitation, such as time-variable characteristic, difficult realization and high cost, mathematical simulation of unsteady ventilated supercavitation is studied. Based on the principle of independence of cavity sections expansion(Logvinovich′s principle), an model of unsteady ventilated supercavitation is established, and corresponding simulation method is presented. The factors influencing supercavitation shape are simulated dynamically. Consequently, the supercavitation′s shape change regularity and its relative position to underwater vehicle surface are obtained at different ventilation parameters and moving parameters, and the requirements of cavity close position for satisfying vehicle high-speed steady motion are proposed. This study may offer a reference for designing ventilating system and running capability of an underwater high-speed vehicle.

underwater high-speed vehicle; unsteady; ventilated supercavitation; mathematical simulation

TJ630.1

A

1673-1948(2012)05-0321-05

2012-03-30;

2012-06-06.

王改娣(1964-), 女, 研究员, 主要从事鱼雷总体性能和弹道仿真建模研究工作.

(责任编辑: 陈 曦)