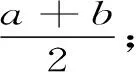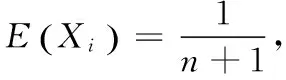数学期望的计算方法
高显彩,张丽慧
(1宿州学院 数学与统计学院,安徽 宿州 234000;2宿州市 第二中学,安徽 宿州 234000)
数学期望简称期望,又称均值,是随机变量最基本的数字特征之一, 它反映了随机变量的某个侧面的平均性,而且随机变量的其他数字特征都是由数学期望来定义的,因此对随机变量的数学期望的计算方法的研究与探讨具有很深的实际意义.本文通过一些具体的例子说明不同的计算方法在不同情况下的应用,以达到计算最简化的目的.
1 定义法
例1[1]设随机变量X服从均匀分布,求它的数学期望.
解由于X~U(a,b),则它的密度函数为
其他
则根据定义它的数学期望为
可见,均匀分布的数学期望位于区间[a,b]的中点,即均匀分布具有对称性.
2 利用数学期望的性质
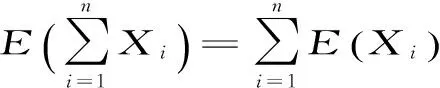
例2[2]将n个球随机地放入M个盒子中去,设每个球放入各个盒子是等可能的,求有球盒子数X的期望.

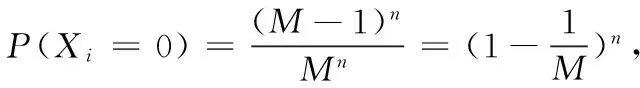
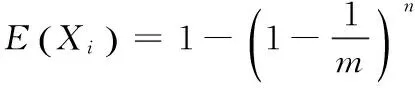
例3[5]设X~B(n,p),求E(X)
解方法一:根据数学期望的定义有
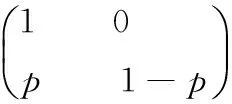
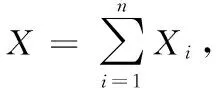
3 利用逐项微分法
这种方法是对于概率分布中含有参数的随机变量而言的,我们可以通过逐项求微分的方法求解出随机变量的数学期望.
例4[3]设随机变量X~Ge(p),求E(X).
解因为X~G(p),故P(X=k)=p(1-p)k-1其中0 令q=1-p,利用逐项微分可得X的数学期望为 例5 设随机变量服从指数分布即X~Exp(λ),求E(X) 例6[1]设随机变量X~N(μ,σ2),证明E(X)=μ. 例7[4]设随机变量X~P(λ),求E(X). 例8[3]设随机变量X~N(μ,σ2),求E(X). 解因为随机变量X~N(μ,σ2),则X的特征函数为 例10 设在区间(0,1)上随机地取n个点,以X表示相距最远的两点间的距离,求E(X) 除了上述一些求期望的方法外,还有“利用条件数学期望公式法”,“利用重期望公式法”,“利用α函数或β函数法”等,应用时应灵活应用. 参考文献 [1] 魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,1983 [2] 同济大学应用数学系.概率统计简明教程[M].北京:高等教育出版社,2003 [3] 茆诗松、程依明、濮晓龙.概率论与数理统计教程[M]. 北京: 高等教育出版社,2004 [4] 袁荫棠.概率论与数理统计[M]. 北京:中国人民出版社,1998 [5] 郑章元.应用概率统计(上)[M].南京:南京师范大学出版社,1999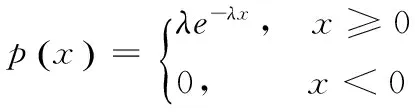
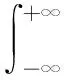
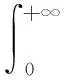
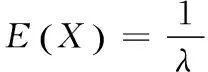
4 利用特殊积分法
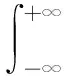

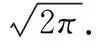
5 利用特殊求和公式
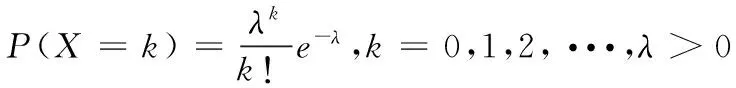
6 利用特征函数
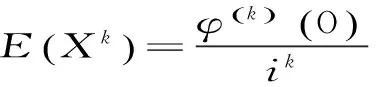
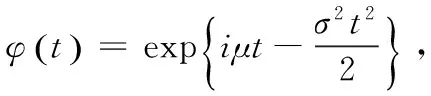
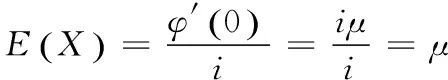
7 利用极坐标变换
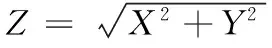
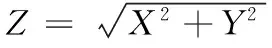
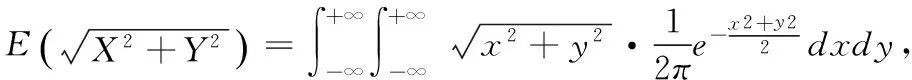
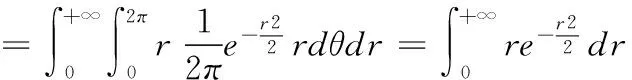
8 利用对称性