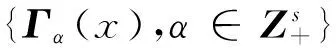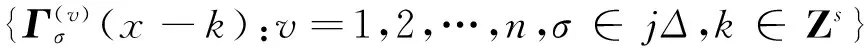具有整数伸缩因子的多变量向量值双正交多小波包
朱玉清, 卫艳荣, 程正兴
(1.南阳理工学院 数理学院 河南 南阳 473004; 2.济源职业技术学院 基础部 河南 济源465650; 3.西安交通大学 理学院 陕西 西安 710049)
0 引言
多小波由于拥有良好的特性而被广泛地应用在图像压缩、信号处理[1]、求解积分方程与微分方程等方面.向量值小波是一类广义多小波.Xia和Suter[2]引入向量值正交小波的概念.文献[3]讨论了多重向量值双正交小波的存在性及其构造.文献[4]运用多重向量值双正交小波变换研究海洋涡流现象.为了改变小波基的频域局部性,人们引入一元正交小波包的概念.杨建伟等[5]将一元正交小波包的概念推广到多元小波包的情形,给出多元正交小波包的定义.文献[6]进一步给出多变量多重双正交小波包的定义、构造及其性质.受文献[3,6]的启发,本文给出具有伸缩因子aIn2≤a,n∈Z的多变量向量值双正交小波包的定义及其构造,讨论了它们的性质.利用向量值小波包,构造了空间L2(Rs,Cn)的一个新的基底.
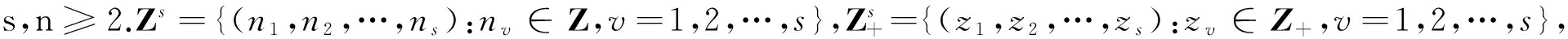

(1)

称多元向量值函数列{ћv(x-k):v=1,2,…,n}k∈Zd为子空间V的Riesz基,如果它们满足下列两个条件:(i)对任意Γ(x)∈V,都存在唯一的常数序列b={bv(k):v=1,2,…,n}k∈Zd使得

(ii)存在常数0 多分辨分析方法是构造小波的常用方法.先引进多元向量值函数空间L2(Rs,Cn)的多元向量值多分辨分析.设ћj(x)=L2(Rs,Cn),j=1,2,…,n分别满足下列n个方程, (2) 其中{bi,j(k),i,j=1,2,…,n}是一个有限支撑数列.记H(x)=(ћ1(x),ћ2(x),…,ћn(x)),根据矩阵理论,方程(2)等价于方程(3), (3) (4) 定义一个闭子空间序列Uj⊂L2(Rs,Cn)为 (5) (6) (7) (8) (9) (10) L2(Rs,Cn)=U0⊕j≥0Wj=⊕j∈ZWj=⊕j∈Z(⊕μ∈ΛWj(μ)). (11) 引入多变量向量值双正交多小波包.然后,讨论它们的性质.引入记号 (12) (13) 为了讨论多变量值双正交多小波包的性质,给出2个引理. 证明由于R2=Uλ∈Zs([0,2π]s+2πλ),而且当λ1,λ2∈Zs,λ1≠λ2时,([0,2π]s+2πλ1)∩([0,2π]s+2πλ2)=Φ. (14) AΩσ=⊕μ∈Λ0Ωmσ+μ,j∈Z+; (15) (16) 参考文献: [1] 刘再涛,魏本征,柳澄.一种基于视觉感知的复合医学图像分割算法[J]. 郑州大学学报:理学版,2011,43(1): 57-61. [2] Xia X G, Suter B W. Vector-valued wavelets and vector fiter banks[J]. IEEE Trans Signal Processing, 1996 ,44(3): 508-518. [3] Bacchelli S, Cotronei M, Sauer T. Wavelets for multichannel signals[J]. Adv Appl Math, 2002,29: 581-598. [4] 冷劲松,程正兴. a尺度多重双正交小波包的L2R分解[J]. 工程数学学报,2004,21(3): 391-396. [5] 杨建伟,程正兴,杨守志.任意矩阵伸缩的正交小波包[J].高等学校计算数学学报,2003,25(1):91-96. [6] 陈清江,程正兴,冯晓霞.高维多重双正交小波包[J].应用数学, 2005,18(3):358-364. [7] 张广耀, 李镇. 一个n×n矩阵特征值问题的迹公式及其应用[J]. 郑州大学学报:理学版,2010,42(4): 18-23.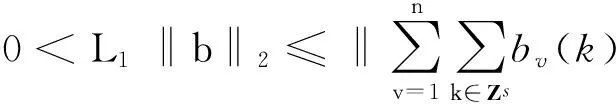
1 多元向量值多分辨分析

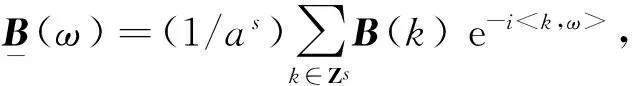
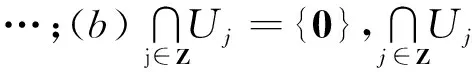


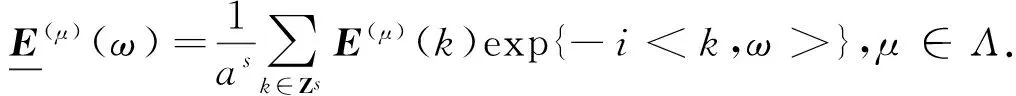

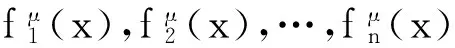
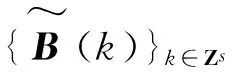

2 多变量向量值双正交多小波包的概念与性质