扰动Korteweg-de Vries方程的Darboux变换及其显式解

何国亮， 杨本朝

(1.郑州大学 数学系 河南 郑州 450001; 2.信息工程大学 信息工程学院 河南 郑州 450002)

0 引言

近年来, 非线性偏微分方程在物理学、动力学、生物学等诸多学科领域都得到了广泛应用, 尤其是物理和工程中的许多现象都可以用非线性微分方程来刻画. 因此, 如何求得这些方程的精确解或者近似解便成为一个重要的研究课题[1]. 目前, 可以借助于多种方法来构造非线性偏微分方程的显式解, 例如Hirota双线性方法[2]、代数几何方法[3]、齐次平衡法和半逆法[4-5]以及Darboux变换方法[6-7]等, 其中Darboux变换法是求解非线性偏微分方程最有效的途径之一.

本文从具有两个位势的4×4矩阵谱问题出发, 利用规范变换, 得到了扰动Korteweg-de Vries (KdV)方程[8]

ut=-uxxx+6uux;vt=-vxxx+6(uv)x

(1)

的Darboux变换, 并由此构造出扰动KdV方程的一些显式解.

1 扰动KdV方程的Darboux变换

构造扰动KdV方程的Darboux变换. 首先, 考虑矩阵谱问题[9]

χ

(2)

和辅助谱问题

χt=V(s,λ)χ=(Vij)4×4χ,

(3)

其中，

V11=V33=-ux，V12=V34=2u+4λ，V21=V43=-uxx+2u2+2uλ-4λ2，
V22=V44=ux，V13=V14=V23=V24=0，
V41=-vxx+4uv+2vλ，V42=vx，V32=2v，V31=-vx,

而u,v是两个位势,λ是常值谱参数,χ=(χ1,χ2,χ3,χ4)T，s=(u,v). 由相容性条件χxt=χtx，可得零曲率方程Ut-Vx+[U,V]=0，即扰动KdV方程(1).

(4)

T11=T33=a+λ,T12=T34=d,T21=T43=ax+du-dλ,T22=T44=dx+a+λ,T31=b,T32=c,T41=bx+uc+dv-cλ,T42=cx+b,T13=T14=T24=T23=0,

直接计算得

detT=[λ2+(2a+dx+d2)λ+adx+a2-dax-ud2]2,

(5)

其中a,b,c,d为待定函数.假设λ1,λ2满足detT=(λ-λ1)2(λ-λ2)2=0,显然当λ=λj(j=1,2)时,Φ的列向量线性相关, 由此可得线性代数系统

(6)

(7)

考虑线性变换

(8)

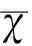
(9)

(10)

(11)

2 扰动KdV方程的显式解

(12)

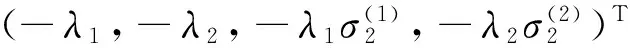
Ⅰ)选取扰动KdV方程(1)的一组平凡解u=0,v=0, 则(2)和(3)式约化为

(13)

基解矩阵为

(14)

再由(7)式可得

由Darboux变换(11), 可得扰动KdV方程(1)的一组显式解

(15)

Ⅱ)选取扰动KdV方程(1)的平凡解u=1,v=0，则(2)和(3)式约化为

(16)

可选取基解矩阵为

(17)

再由(7)式可得

由Darboux变换(11)，可得扰动KdV方程(1)的一组显式解为

(18)

Ⅲ)选取扰动KdV方程(1)的一组平凡解u=1,v=1，则(2)和(3)式约化为

(19)

基解矩阵取为

(20)

再由(7)式可得

由Darboux变换(11)，可得扰动KdV方程(1)的一组显式解

(21)

参考文献：

[1] Lamb G L. Elements of Soliton Theory[M]．New York：Wiley，1980．

[2] 马云苓，耿献国．两类(2+1)-维孤子方程的显式解[J]．广西师范大学学报：自然科学版，2011，29(2)：45-49．

[3] Geng Xianguo，Cao Cewen．Decomposition of the (2 + 1) dimensional Gardner equation and its quasi periodic solutions[J]．Nonlinearity，2001，14(6)：1433-1452．

[4] 刘法贵，冯国鑫．高阶非线性Schrodinger 方程的精确解[J]．郑州大学学报：理学版，2011，43(4)： 1-4．

[5] 刘倩，周钰谦．二维Klein-Gordon-Zakharov方程的显式精确解[J]．四川师范大学学报：自然科学版,2009，32(6)：771-774．

[6] 李雪梅，牛亏环．广义TD族及一些非线性演化方程的显式解[J]．郑州大学学报：理学版，2007，39(3)：1-6．

[7] Geng Xianguo，Ren Hongfeng，He Guoliang，et al．Darboux transformation for a generalized Hirota-Satsuma coupled Korteweg-de Vries equation[J]．Phys Rev E，2009，79(5)：056602．

[8] Ma Wenxiu，Fuchssteiner B．The bi-Hamiltonian structure of the perturbation equations of the KdV hierarchy[J]．Phys Lett A，1996，213(1/2)：49-55．

[9] Ma Wenxiu，Geng Xianguo．New completely integrable Neumann systems related to the perturbation KdV hierarchy[J]． Phys Lett B，2000，475(1/2)：56-62．