FRP约束混凝土组合柱滞回性能的有限元分析*

吴智林 姜绍飞 吴兆旗



FRP约束混凝土组合柱滞回性能的有限元分析*

吴智林 姜绍飞 吴兆旗

福州大学土木工程学院

为研究FRP-PVC管钢筋混凝土的抗震性能，本文基于OpenSEES中的纤维模型对FRP-PVC管钢筋混凝土压弯构件的P-Δ滞回曲线进行有限元模拟，通过合理确定截面纤维的滞回本构模型，可得到与试验数据吻合较好的数值模拟结果。分析FRP包裹层数、FRP条带间距等参数对约束柱抗震性能的影响，结果表明：包裹层数主要是对试件的变形能力有影响，对试件的峰值荷载值影响不大。BFRP存在使用效率的问题，包裹7层纤维布与包裹8层纤维布的效果相当；随着条带间距的增大，试件的极限荷载和极限变形均减小，荷载下降段的下降幅度越大。条带间距取20～30mm较为合理。

FRP-PVC管 抗震性能 OpenSEES 有限元分析

0 引言

FRP-PVC管混凝土柱是一种新型的结构体系[1-2]，它由轻质、经济、高性能、耐久性好的材料组成。该结构是在PVC管外面按照一定的环箍间距缠绕FRP形成FRP-PVC管，在进行包裹时，用专门的环氧树脂等粘结材料将FRP片材粘贴于结构表面。再利用FRP-PVC管作为模板，在其内浇筑混凝土而形成的。该新型构件可以充分利用PVC和FRP两者的材料优势。FRP环箍可以对核心混凝粘土提供有效的横向约束，然后通过PVC管将约束应力均匀地分布到混凝土柱。PVC管有一定的刚度，施工时可作为模板；FRP、PVC两种材料均有良好的耐久性，故FRP-PVC管对核心混凝土有保护作用，使其在各种环境中免受侵蚀[3]。

FRP-PVC管混凝土作为一种新兴的结构形式，目前的研究大多集中在这种形式短柱静力性能的试验研究和理论研究，以及耐久性研究。对FRP-PVC管混凝土柱抗震性能的研究在国内外鲜见报道。对该新型结构抗震性能的研究有助于该类结构在工程中的推广应用。相关试验研究[2,4]表明FRP-PVC管约束可以有效提高混凝土的强度和极限应变。混凝土极限应变的提高对抗震性能提高很重要，它使得柱在非弹性变形过程中能达到更大的延性水平。

借助通用有限元软件ANSYS、ABAQUS等来进行组合柱的有限元分析时，常用方法是用实体单元模拟混凝土，用实体单元或壳单元模拟外包钢或外包FRP等材料，材料之间的界面通过接触单元模拟。基于实体单元和壳单元的有限元分析方法，自由度数量大，计算和分析较为复杂[5]，另一种方法是纤维模型法。该方法既能基于合理的基本假定，在一定精度下模拟组合构件的力学性能，并且自由度少，更便于结构整体的受力分析。本文拟采用基于纤维模型的Open SEES软件对FRP-PVC管约束混凝土压弯构件的滞回性能进行有限元分析，为设计和研究FRP-PVC管约束混凝土结构的抗震设计提供参考依据。

1 有限元模型的建立

1.1 模型简介

OpenSEES（Open System for Earthquake Engineering Simulation，开源的地震工程模拟系统）软件主要用于分析结构在地震作用下的反应，其功能包括线性分析，静力和动力非线性分析，特征值计算等功能[6]。本文数值模拟采用OpenSEES中的非线性梁柱单元（nonlinear beam column）。此单元是基于纤维模型的非线性单元，可应用于杆系结构的静力与动力非线性分析并考虑P-Delta效应。

采用OpenSEES软件作为仿真平台来对FRP-PVC管钢筋混凝土圆柱进行滞回模拟。基于OpenSEES中的纤维模型进行建模，采用半柱高悬臂柱模型，选用nonlinear beam column单元，沿半柱高分布6个上述单元，再将纤维截面的特性赋予上述所有单元。建立纤维模型时，没有对FRP-PVC外包管进行建模，而是在建立核心约束混凝土本构关系的时候考虑了外包管对核心混凝土的约束效应。FRP-PVC管钢筋混凝土圆柱单元划分及纤维截面组成如图1所示。

图1 纤维模型示意图

1.2 材料的滞回本构模型

钢筋本构关系采用可考虑等向应变强化的Giuffré- Menegotto-Pinto本构模型[7]，该模型与钢筋反复加载试验结果吻合较好。建模时，采用Steel02描述，屈服强度及弹性模量按材料试验结果取值，钢筋强化系数取0.05。

混凝土本构采用OpenSEES中的Confined Concrete01描述，具体应用时先根据BGL模型[8]计算箍筋和FRP条带包裹PVC外包管双重约束作用下的横向约束应力f。

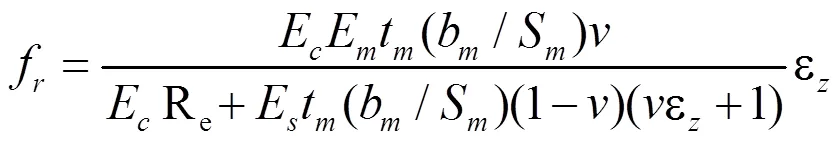
式中，εz为柱轴向压应变；为混凝土泊松比；为柱圆截面半径；t为FRP包裹厚度；b为FRP条带宽度；S为FRP条带间距。E、E、E为材料弹性模量，下标c代表混凝土、m代表外包FRP、s代表钢筋。

再根据计算得到的横向约束应力，采用Attard和Setunge等人提出的约束混凝土本构模型[9]计算得到混凝土应力-应变本构模型。

进行有限元分析时，约束柱底部视为固定端，另一端不约束位移，不考虑粘结滑移和剪切变形的影响。柱首先承受轴力，随后在柱顶施加水平往复位移，选用Newton-Raphson迭代方法控制位移收敛并求解非线性方程，同时考虑P-Δ效应的影响。

2 数值模拟与试验结果的比较

2.1 试验介绍

福州大学近期完成了一组3个FRP-PVC管约束钢筋混凝土压弯构件的滞回试验。压弯构件加载装置同文献[10]中压弯构件滞回加载装置。试件设计为：长度均为1500mm，PVC管的外径均为200mm，PVC管壁厚均为4.5mm，FRP环箍宽度和环箍间距均为30mm，在跨中300mm范围内设置FRP全包裹，目的是对夹具位置进行加强处理。所有试件的混凝土强度等级采用C30，纵筋沿着环向布置612，配筋率为2.01%，箍筋均配置6@100。其他参数见表1，其中B0试件为无FRP包裹。

表1 试件的部分参数

混凝土28天混凝土立方体抗压强度f=32.6MPa，弹性模量E=24.1GPa。BFRP、箍筋、纵筋等材料的实测力学性能见表2。

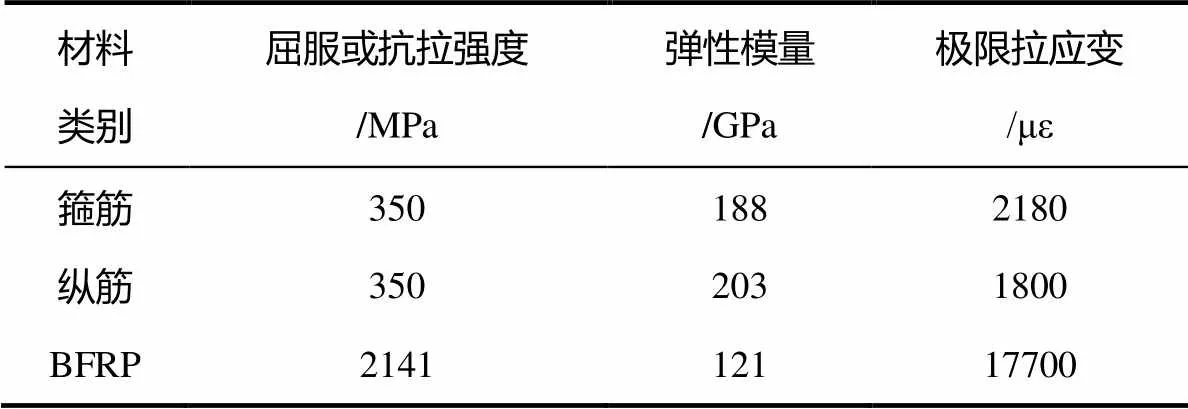
表2 部分材料的力学性能

进行加载试验时，先施加恒定轴力，然后施加侧向的往复荷载。采用位移控制加载，试件屈服前以1mm为步长加载，在试件达到屈服之后，改成以屈服位移∆y的整倍数为级差进行控制加载。即加载位移幅值分别为1.0，2.0，3.0，4.0，5.0，6.0……∆y，2∆y，3∆y，4∆y，5∆y……（mm）。屈服前一般每级荷载反复一次，屈服以后反复三次。当骨架线荷载下降到极限荷载的50％或位移达到3倍峰值荷载对应的位移以上时，试验结束。

2.2 数值模拟与试验结果的比较

验证数值模型时，材料参数等均按照材料性能试验实测值来输入，数值模拟时施加的轴压力以及侧向往复位移均按照试验实际的加载制度来输入。试验结果与利用OpenSEES进行有限元模拟的结果如图2所示。图2表明，模拟结果与实测的P-Δ滞回曲线基本吻合，卸载路径及再加载路径均吻合较好，只是模拟结果曲线饱满度与实测曲线相比较稍差。

滞回曲线骨架线模拟情况如图3所示。图3表明，模拟的P-Δ滞回曲线骨架曲线与实测曲线相比吻合良好，但极限强度比试验结果稍低。总体而言，由于整体吻合良好，所以可以进一步利用该模型进行参数分析。

图2 数值模拟与试验结果的比较

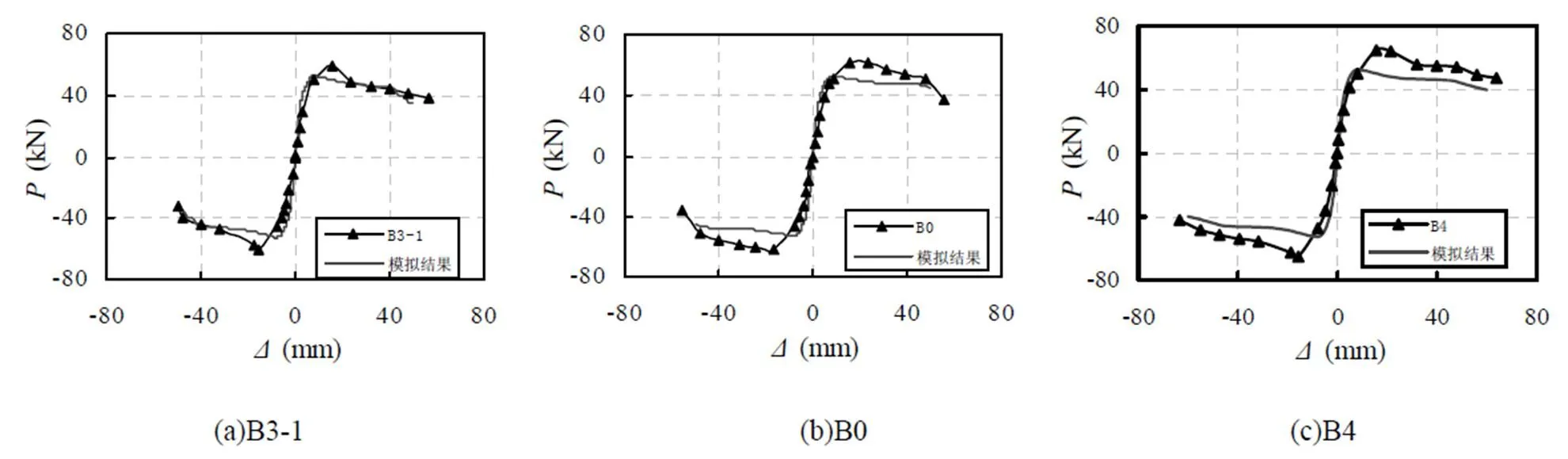
图3 数值模拟与试验结果的骨架曲线比较

3 参数影响分析

3.1 FRP包裹层数

采用B3-1试件作为基本模型进行参数分析，考虑玄武岩纤维BFRP包裹层数的影响，其它参数保持不变，结果如图4所示。包裹层数主要是对试件的变形能力有影响，对试件的峰值荷载值影响不大。随着包裹层数的增加，试件的极限位移不断增大，延性提高；但极限位移的提高幅度在不断减小，包裹7层纤维布与包裹8层纤维布的效果相当。这说明BFRP存在使用效率的问题，应根据约束柱的延性要求来确定合理的包裹层数。

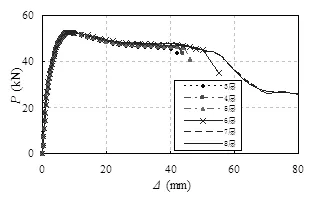
图4 FRP包裹层数的影响

3.2 FRP条带间距

采用B3-1试件作为基本模型进行参数分析，条带宽度为30mm，考虑条带间距的影响，其它参数保持不变，结果如图5所示。条带间距的变化对试件P-Δ骨架曲线的荷载下降段差异较大，对弹性段受力性能影响较小。随着条带间距的增大，试件的极限荷载和极限变形均减小，荷载下降段的下降幅度越大，条带间距为40mm时的极限荷载有一个较大的下降；当条带间距为20mm、30mm时，试件的极限荷载和极限位移相差不大，且极限荷载较为稳定、无很明显下降，说明条带间距取20~30mm较为合理。

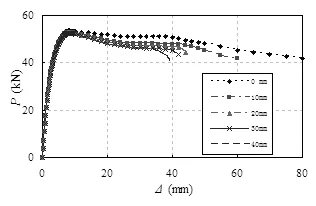
图5 FRP条带间距的影响

4 结论

本文对FRP-PVC管钢筋混凝土压弯构件滞回性能进行了数值分析，探讨了FRP包裹层数、FRP条带间距对构件滞回性能的影响规律，得到以下主要结论：

(1)采用OpenSEES程序分析压弯构件滞回性能时，通过合理确定截面纤维的滞回本构模型，可得到与试验数据吻合较好的数值模拟结果；

(2)包裹层数主要是对试件的变形能力有影响，对试件的峰值荷载值影响不大。BFRP存在使用效率的问题，包裹7层纤维布与包裹8层纤维布的效果相当。

(3)随着条带间距的增大，试件的极限荷载和极限变形均减小，荷载下降段的下降幅度越大。条带间距取20~30mm较为合理。

[1] 于峰，武萍．新型组合结构柱性能研究[J]．工业建筑，2009，39(2)：97-99．

[2] 姜绍飞，吴兆旗，杨启斌，等．FRP约束的新型组合结构力学性能研究[J]．哈尔滨工业大学学报，2010，42(s1)：61-63．

[3] 于峰，牛荻涛，武萍．PVC-FRP管混凝土结构实际应用的可行性研究[J]．建筑科学，2007，23(11)：102-104．

[4] 戴甜杰，姜绍飞，吴兆旗．BFRP-PVC管混凝土短柱轴压试验研究[A]//第二届海峡两岸土木工程建设与管理研讨暨地震模拟振动台台阵试验技术交流会论文集[C]．2011．

[5] 陈学伟，韩小雷，季静，等．基于纤维模型的CFRP布加固混凝土柱有限元分析[J]．工业建筑，2007增刊：149-152．

[6] OpenSee．Open system for earthquake engineering simulation，2009．http://opensees.berkeley.edu/．

[7] Menegotto M， Pinto P E．Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[R]．Lisbon：International Association for Bridge and Structural Engineering，1973．

[8] Braga F，Gigliotti R，Laterza M．Analytical stress–strain relationship for concrete confined by steel stirrups and/or FRP jackets[J]. Journal of Structural Engineering, 2006,132(9):1402-1416．

[9] Attard M M， Setunge S．Stress-strain relationship of confined and unconfined concrete[J]．ACI Materials Journal，93(5)：432-442．

[10] 韩林海．钢管混凝土结构——理论与实践[M]. 第二版．北京：科学出版社，2007．

国家“十二五”科技支撑计划(2012BAJ14B05）；福建省杰出青年基金(2009J06027)；住房和城乡建设部项目(2009-K2-40)。