以正辛烷为介质离心分离碳同位素

周明胜，李 梁，徐燕博，程维娜

（清华大学 工程物理系，北京 100084）

碳元素有12C及13C两种稳定同位素。12C的天然丰度为98.89%，13C为1.11%。自然界中还有极微量的放射性同位素14C。其中，13C在临床诊断、药物研究等方面有着重要应用，如13C呼吸检测法用于幽门螺旋杆菌诊断［1］已被欧美国家普遍接受。随着技术进步和社会发展，其应用还会愈加广泛。13C的具体应用对其丰度有一定要求。为了获得丰度较高的13C，需要对天然碳同位素进行分离。目前用于13C分离的主要是精馏方法，美国的CIL、ISOTEC公司（CO低温精馏法）及日本的Tokyo Gas公司（CH4低温精馏法）已实现13C在工业上的生产，年产量均在100 kg以上［2］。低温精馏方法的优点是通量大，适于大规模生产，缺点是能耗较大。因此目前13C的价格比较昂贵。气体离心法的特点是能耗低，分离系数较大，适于重同位素分离。欧洲的Urenco［3］通过气体离心机分离了碳、硅等多种同位素，说明离心法在分离稳定同位素方面具有可行性。因此，通过实验研究13C的离心分离，具有重要的意义。

1 分离介质的选择

离心机是高速旋转的设备，对分离介质有较高要求。工作介质一般应满足以下条件：1）具有一定饱和蒸汽压（＞665 Pa）；2）相对分子质量不小于70；3）在570 K以下具有热稳定性。除此之外，还要考虑原料成本、尽量不引进新的同位素影响等因素。因此，找到合适的分离介质是实现离心分离的第一步，也是关键的一步。在调研初期，希望能找到一种较理想的分离介质，利用它可以将13C直接分离到较高丰度。但是通过大量调研工作之后，并没有找到这种较为理想的分离介质，因此调整了调研方向，重点寻找可以将天然13C浓缩10倍以上的分离介质。根据调研结果，选择了正辛烷（C8H18）作为分离介质。正辛烷的平均相对分子质量为114.22，常温下为液态，饱和蒸汽压为1.33 k Pa（19.2℃），具有化学稳定性，可满足上述介质选择的要求。此外，正辛烷作为分离介质还有以下两个优势：1）正辛烷是汽油的主要成分，价格低廉，可大幅降低分离原料成本，并且废料还可完全被再利用；2）碳含量达84.21%，有利于提高碳的分离效率。

C8H18中还含有近15.8%的氢元素，但其同位素氘的天然含量很低，可不予考虑；此外14C的自然丰度也极低，也可忽略不计。在此前提下，利用天然碳元素的同位素丰度分布，通过排列组合计算，可知天然正辛烷有9种不同组分，其各自的质量分数列于表1。

根据表1的计算结果可以看到，相对分子质量为115的组分含有1个13C原子，其质量分数约为8.2%。相比之下，相对分子质量大于115的组分含有更多的13C原子，但它们的质量分数都很小，如果将它们中的某一种组分作为目标组分，分离起来比较困难，而且必然要耗费大量原料。考虑到分离的可行性和经济性，将相对分子质量为115的组分作为目标组分更合适。而在相对分子质量为115的组分中，13C只占其含碳总量的12.5%，因此，以正辛烷为分离介质可将13C浓缩至12%左右。如果要进一步浓缩，则要将正辛烷转化成碳的其它化合物。

表1 天然正辛烷各组分的相对分子质量及其质量分数

2 单机分离实验研究

为了验证离心机单机分离正辛烷的可行性，并且掌握相关的单机分离规律，首先需要进行单机分离实验。

2.1 多元分离理论基础

同位素分离的理论体系分为二元分离和多元分离两种情况，两者在一些基本的定义上就有一定的区别。正辛烷有9种组分，所以它的分离属于多元分离的范畴。从近年来国内外的研究来看，对多元分离下的一些基本定义尚未有统一的结论，其理论体系也更为复杂。本文只针对本实验研究涉及到的全分离系数做一个简单介绍。对于全分离系数，一般采用Kai［4］给出的定义：

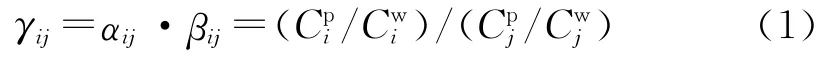
（1）式中：γij、αij、βij分别表示第i、j种组分的全分离系数、轻馏分分离系数、重馏分分离系数；Cpi、Cwi和Cpj、Cwj分别为精料、贫料中第i、j种组分的丰度。

现有的研究［5］表明，第i、j种组分之间的全分离系数γij与它们的相对分子质量之差ΔMij存在如（2）式所示的指数关系：

（2）式中，γ0称为基本全分离系数。在不改变分离工况的前提下，γ0是一个常数，它反映了单机的分离性能。单机实验研究的重点之一就是确定离心机在不同工况下分离正辛烷的基本全分离系数。

2.2 实验装置和实验方法

采用的分离设备示于图1。由图1可见，分离设备包括分离单元和供取料系统两部分。其中分离器采用的是国产离心机，供取料系统则是由实验室自行设计。分析设备采用的是MAT－281质谱仪。实验所用正辛烷原料的化学纯度为99.99%。

图1 单机分离碳同位素实验原理图

实验时，通过供取料系统将正辛烷以一个稳定的流量供入离心机中分离。通过调节供料压强而控制供料流量。由于常温下正辛烷的饱和蒸汽压只有1 333.22 Pa，而料瓶的体积较小，很难维持一个稳定的供料流量。为解决这一问题，实验室中采取的办法是在供料瓶处并联一个77 L的大容器（称为稳压容器），以保证供料流量的稳定。进一步的还可以在稳压容器上再外接一个装有液态正辛烷的料瓶（称为原料瓶），其中的正辛烷可连续不断地挥发至稳压容器中，以保证连续稳定的供料气流。通过分离实验证明，这种方法是可行的。在实际生产中，也可以根据这一原理来实现稳定供料。

供料流经过离心机分离后出来两股流，其中轻组分得到浓缩的称为精料，重组分得到浓缩的称为贫料。实验时，采用液氮冷冻的方法将分离出来的精料和贫料分别收取至不同料瓶中。分离状态达到稳定后，分别对精、贫料进行取样。取样也采用液氮冷冻的方法。为了判断分离状态达到稳定所需要的时间，研究中采取在一个分离工况下、不同的时间点多次取样，进行对比分析，最后确定了合适的取样时间点。从压强监测仪表上观察，单机分离的流场达到稳态只需几分钟。但从保守角度出发，一般在1.5 h后才开始取样。为了验证此时分离状态已经稳定，本工作在一个分离工况下，分别于供料分离后1.5、2、3、4 h等多个时间点取样，进行对比分析。只要分离达到稳态之后，不管是何时取样，其质谱分析结果应该是一致的。通过大量这样的实验对比，基本可以确认在供料1.5 h后取样是可行的。

分离实验结束后，利用MAT-281质谱仪对正辛烷的精料、贫料样品进行组成分析，由此得到精料、贫料中不同组分的质量分数。通过进一步计算，最后得到分流比和基本全分离系数等重要基本参数。

3 结果与讨论

利用上述实验装置，改变供料流量、滞留量等参数，在不同的工况下进行分离，达到稳定后取样分析，由此得到分流比和基本全分离系数等基本参数的一系列实验数据，结果列于表2。由表2可知，在实验涉及到的调节范围内，γ0最高可以达1.13。

需要注意的是，由于天然正辛烷中相对分子质量大于115的组分质量分数极小，经过一次分离后变化也很有限，质谱难以检测或相对误差较大。因此，在计算分析时，只采用了相对分子质量为114和115两种组分的质谱数据。

利用上述单机数据，可以对13C离心分离级联做一个简单的估算。取γ0＝1.13，要求得到的13C丰度约为10%，采用文献［6］提出的相对丰度匹配级联的方法进行估算。计算时忽略相对分子质量大于118的组分，取相对分子质量为115的组分作为目标组分，要求其质量分数在精料中不高于5%，在贫料中不低于75%。以关键相对分子质量M＊为优化自变量，级联总流量LΣ最小为优化目标，计算结果为：M＊＝114.42时，LΣ／F 最小为279.72，此时的级联总长度为N ＝75级，供料级位置在NF＝69级，贫料中13C丰度为10.83%，贫料流量与供料流量比W／F＝4.26%，供、精、贫料流中不同组分的质量分数分布列于表3。

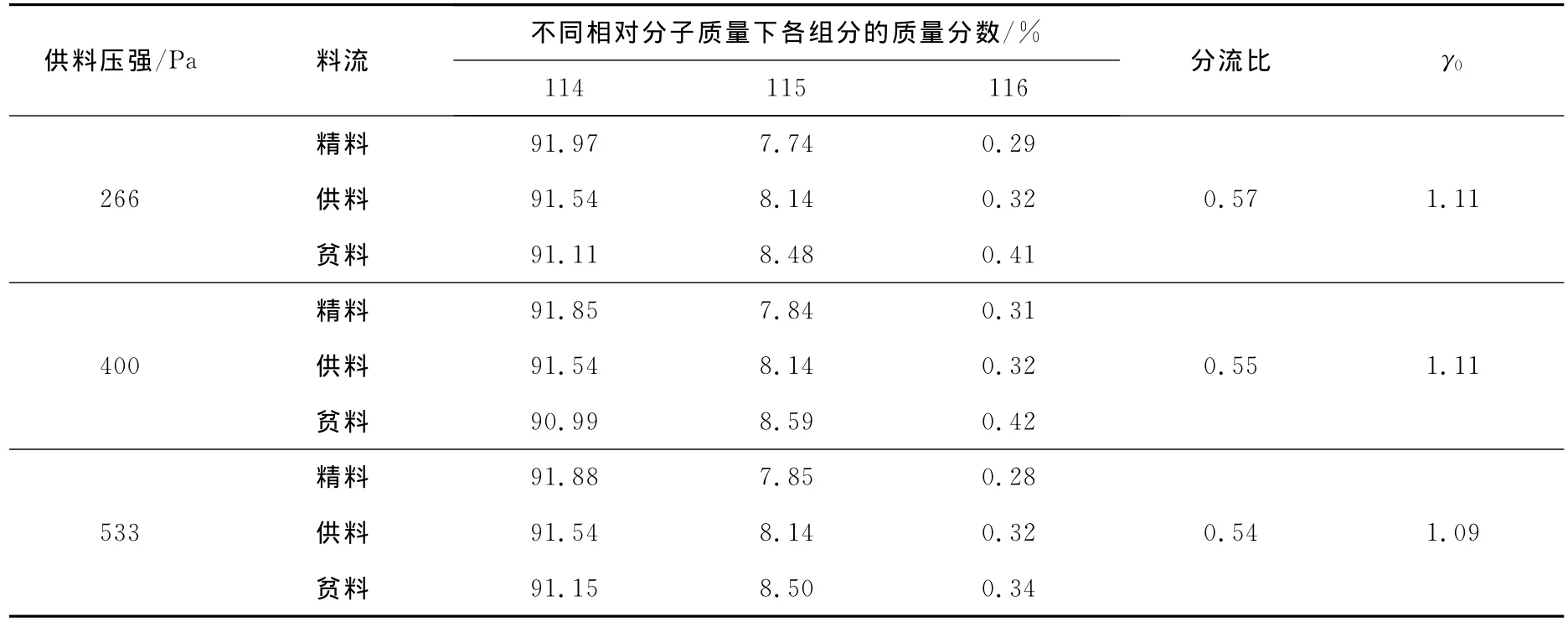
表2 正辛烷单机部分分离实验结果

表3 准理想级联分离正辛烷的计算结果

准理想级联模型虽然与实际有一定差距，但通过这种计算可以对分离级联做一个初步估计。从上述计算结果可知，以正辛烷为介质，通过级联分离可以将13C浓缩至约11%。从计算结果还可知，分离所需的级联长度偏长。可考虑采用一个短级联和一长级联组合，短级联大量处理正辛烷原料，长级联则进一步对短级联所得的产品进行分离，将13C浓缩至11%左右。这方面的研究工作目前正在进行。

4 结 论

通过以正辛烷为介质离心分离碳同位素的研究，可以得出两点结论。

1）以正辛烷为介质离心分离13C是可行的，并且还得到了不同工况下的基本全分离系数、分流比等重要参数，基本掌握了其单机分离性能。

2）以正辛烷为介质离心分离13C有其局限性，由于C8H18不同组分的构成特点，结合分离的可行性和经济性考虑，只能将13C浓缩至约12%。

如果能将正辛烷转化为合适形态的碳化合物，进一步进行离心分离，得到高丰度的13C也是可能的。

［1］ Kr u mbiegel P，Rolle-Kampczyk U，Lieber geld P，et al.Towar ds an inhalative13C breath test method ［J］.Isotopes in Environ mental and Health Studies，2002，38（2）：65-70.

［2］ 李虎林.碳、氮、氧稳定同位素生产技术现状及发展趋势［C］／／全国稳定同位素新技术开发与应用交流研讨会，上海：中国核学会同位素分会、上海稳定性同位素工程技术研究中心，2011：1-12.

［3］ Urenco.Stable Enriched Isotopes ［EB／OL］.［2011-05-18］.htt p：／／www.urenco.co m／content／66／enriched-isotop es.aspx.

［4］ Kai T.Theoretical analysis of Ter nary UF6 gas isotope separation by centrif uge ［J］.Jour nal of Nuclear Science and Technology，1983，20（6）：491-502.

［5］ 郭志雄，应纯同.多组份同位素离心分离的简化计算［J］.清华大学学报：自然科学版，1995，35（3）：71-77.

［6］ Deal Garza A.A generalization of the matched abundance-ratio cassade for multico mponent isotope separation［J］.Chemical Engineering Science，1963，18：73-82.