基于逻辑结构的超前进位加法器的设计*

白首华，胡天彤

(郑州航空工业管理学院，河南郑州450015)

在计算机处理器中，加法器的速度直接决定了整个电路的速度，为了提高整个电路的速度，需要提高加法器的速度。因此，如何设计更高性能的加法器以满足需要成为设计者必须思考和解决的问题。

在了解了半加器和全加器的逻辑公式及构造的基础上，本文引出4位并行的超前进位加法器的设计，再用超前进位链树对16位和32位加法器进行设计，如果将这种方法推导，理论上可以得到并行超前进位的任意位加法器。

1 串行进位链

串行进位链指的是在并行加法器中的进位信号采用串行的方式进行传递，以4位为例:

令 Gi=AiBi，Pi=Ai⊕Bi;推导出

其中:Gi—进位生成函数;Pi—进位传递函数。

可以用与非来实现，以下电路中使用的逻辑门的延时设定［1］:与或非为 1.5ty，或非门的时间延时为 1ty，与非为 ty。那么Gi、Pi形成后共需要2ty×4=8ty，所以每增加一个全加器，进位的时间就要增加2ty。因此，对于n位全加器来说，采用串行进位链，最长的进位时间为2nty。对于多位加法器而言，这种加法器的缺点也是显而易见的。

2 并行超前进位链

通过逻辑电路事先得出加到每一位全加器上的进位输入信号，而不是从最低位开始逐位传递进位信号，就可以有效地提高运算速度，节省运算时间。把实现这种加法的器件叫做超前进位加法器［2］(Carry look-ahead adder，CLA)。超前进位链能够有效减少进位的延迟，它由进位门产生进位，各进位彼此独立，不依赖于进位传播。因此延迟非常小，速度非常高［3］。

理想状态下是n位的全加器的n个进位信号同时产生，但是在实际情况下实行起来有点困难，一般在实际中，采用的是一级分组和二级分组的方法［4］。

2.1 一级分组的超前进位

将n位全加器分成若干小组，在小组内的进位同时产生;小组间采用串行进位。即:组内并行，组间串行。以4位全加器为例，将(1)式分别代入得到公式组(2):

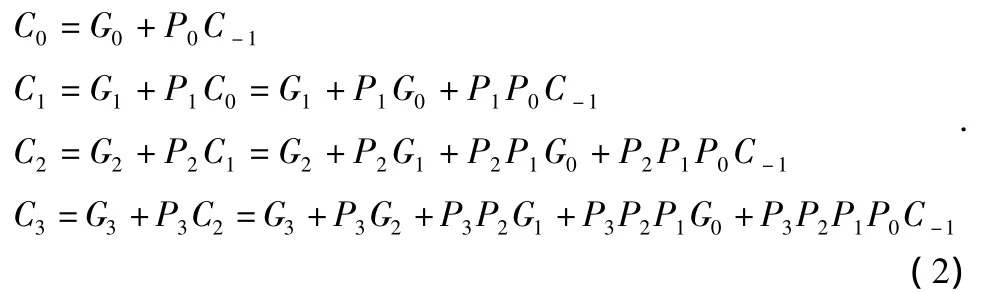
可以看出，进位Ci不是依赖Ci－1，而是均可以直接依赖于向最低位的进位信号C－1，即当C－1输入后，经过与或两级的逻辑延时就可以并行地产生各位向高位的进位信号C0～C3。

所以，在 Gi、Pi形成后，产生全部的进位需要 2.5ty，这有效地缩短了进位信号的传送时间。

所以，以16位的全加器来说:若以4位为一组，分4组，组并行进位，组间串行进位，那么产生全部的 Ci共需2.5ty×4=10ty。

若采用串行链实现全部16位全加器的进位共需要2nty=2 ×16ty=32ty。

2.2 16位两级分组超前进位加法器的设计

以16位为例，4位为一个小组，共4组，组内实现超前进位，组间也可以采用超前进位算法，具体实现过程如下。

图1为两级分组第二级的超前进位链路线图，从图中可以看出，由Ai、Bi和C－1可以直接产生每组内的最高进位信号 C15、C11、C7、C3。图 2 为 Ai、Bi信号产生的逻辑路线图。

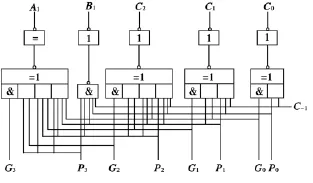
图1 二级超前进位并行进位链路线图

图2 Ai和Bi产生路线图

4位的超前进位模块作为一个小组，每组内都采用超前进位方式，同上所述，可以得出每组内的进位C0～C15，把每组的最高进位表示出来，分别是:

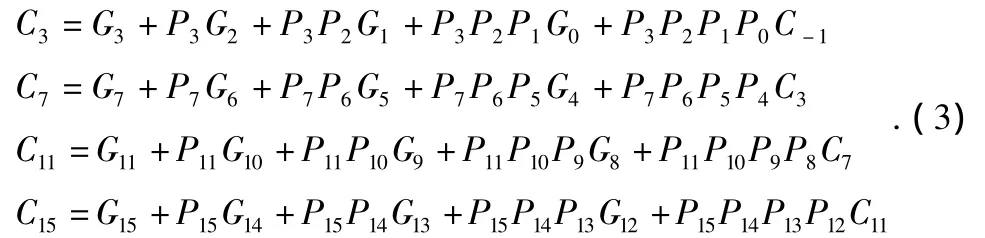
跟前描述一样，可以推出:

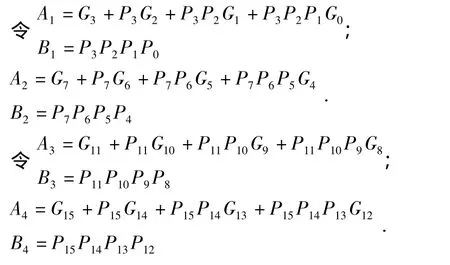
可以推出公式组(4):

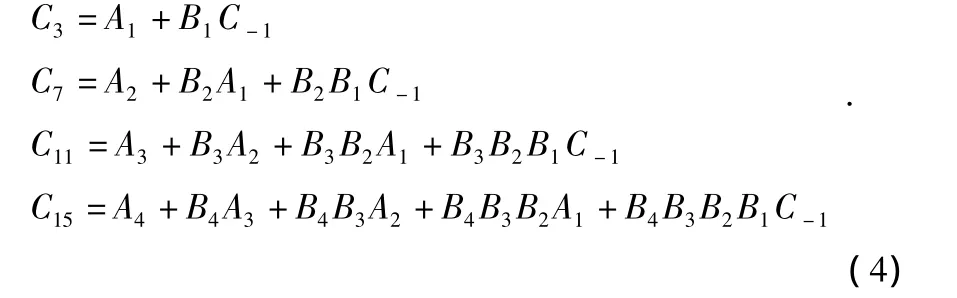
那么，可以得出二级分组的16位超前进位加法器的逻辑结构图。

综上所述，可以推导出各级进位信号的产生时序:

(1)由一级分组可得，当 Gi、Pi、C－1全部产生后，生成Ai、Bi和 C0～C2需要用 2.5ty;

(2)再形成 C15、C11、C7、C3，需要用 2.5ty;

(3)然后产生其余的 C4～C6、C8～C10、C12～C14，需要用2.5ty。

因此，16位的全加器用二级超前进位算法共需要2.5ty+2.5ty+2.5ty=7.5ty。

2.3 32位超前进位加法器的设计

可以采用两级进位算法，将32位全加器分成两个大组(高16位和低16位)。每组又划分四个小组，大组内采用二级超前进位，大组间采用串行进位链实现。

由上述可知，16位二级超前进位全加器需要7.5ty，分析如下:

(1)由 Gi、Pi、C－1形成 C0～C2以及所有 Ai、Bi(i从 1 ～32)需要 2.5ty;

(2)形成 C15、C11、C7、C3，需要用 2.5ty;

(3)再生成 C4～C6、C8～ C10、C12～ C14，需要 2.5ty，由于C15为高16位全加器的组内的C″－1，所以由(2)步骤内的进位生成后，经过2.5ty也生成高一组的C16～C18(相当于第一组的 C0～ C2);Ai、Bi、C15形成后，产生 C31、C27、C23、C19也需要 2.5ty;

(4)C31、C27、C23、C19得到后，经过 2.5ty，形成进位 C30～C28、C26～C24、C22～C20;

因此，由(1)、(2)、(3)、(4)步骤，可以推算出32 位全加器产生所有进位共需要2.5ty×4=10ty，而串行方式下需要2nty=64ty。

超前进位加法器(CLA)通常被认为是最快但是也是最复杂的加法器，它的复杂度与功耗相关，越复杂，功耗就越大［5］。进位的信号产生时序如图3所示。

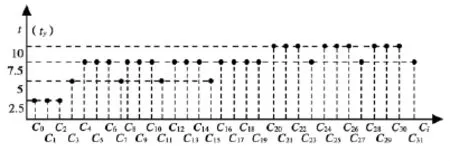
图3 32位CLA的进位时序图

3 结束语

超前进位加法器是为了降低加法器的时间延迟，在设计时采用增大版图面积来提前计算进位信号的设计思想。理想状态下，32位的超前进位加法器运算速度是串行方式下的6倍多。因此，超前进位加法器比传统的串行链式加法器速度上有了极大的提高。而且理论上可以得到并行超前进位的任意位加法器。

［1］毛爱华.计算机组成原理［M］.北京:冶金工业出版社，2004:248－254.

［2］陈光梦.数字逻辑基础［M］.上海:复旦大学出版社，2004.

［3］Pai Yuting，Chen Yukumg.The Fastest Carry Lookahead［C/OL］//Proceedings of the Second IEEE International Workshop on Electronic Design，Test and Applications Los Alamitos，CA，USA:IEEE，2004:434 －436.

［4］［美］Wakerly J F.数字设计原理与实践［M］.第3版.林生，金京林，葛红，等译.北京:机械工业出版社，2003:65－66.

［5］Jia Song，LiuFei.Static CMOS Implementation of Logarithmic Skip Adder［J］，Chinese Journal Of Semiconductors，2003，24(11):1160 －1165.