一类刚性问题的序列分裂方法求解

刘国灿



一类刚性问题的序列分裂方法求解

刘国灿

(湖南文理学院 数学与计算科学学院, 湖南 常德, 415000)

将序列分裂方法应用于一类刚性常微分方程初值问题的求解, 通过理论分析和数例说明分裂方法处理此类刚性问题是收敛的.

刚性问题;序列分裂方法; 相容性

1 问题类描述

考虑如下类型的刚性常微分方程的初值问题:

说明 a. 问题存在刚性, 这意味着实际过程包含多个子过程, 这些子过程相互影响但变化速度相差很大. 文献[1]指出, 人们对刚性问题的认识经历了从线性到非线性的逐步深化与完善的过程. 虽然目前仍无法给出其一个严格的数学定义, 但对其本质形成了如下共识:

(a) 刚性问题欲求的解是慢变的, 但存在快速衰减的干扰[2], 这种干扰使得数值计算复杂化, 在数值稳定性、计算精度及算法实现等方面带来一系列实质困难.

(b) 存在由快速衰减干扰引起的局部坏条件[3].

(c) 刚性问题具有巨大的 Lipschitz 常数.

b. 刚性问题的解包含暂态解和稳态解. 人们感兴趣的主要是稳态解, 因此暂态解至少要衰减到可以忽略不计的时刻. 若试图在整个计算过程中使用显式方法, 整个计算的积分步数将多到在量级上和刚性比相同, 尤其是强刚性问题, 计算量大得惊人, 甚至无法实现. 由此可见刚性问题一般不宜用显式方法求解, 而必须采用稳定性好的隐式方法, 以避免或减缓数值稳定性对步长的苛刻要求.

c. 问题(1)的右端函数既包含有刚性部分, 又包含有非刚性部分. 当然可以对整体用隐式方法数值求解, 但当所考虑的系统非常大的时候, 对函数数值离散所获得的系数矩阵可能不是三对角的或是稀疏矩阵, 这将大大增加数值求解的计算量, 但若能对该部分用显式方法, 一方面可以保证相应的精度要求, 另一方面可以提高计算效率.

d. 对刚性问题的误差分析往往是基于(3)式的, 因为它是基于单边Lipschitz常数的, 对于很多刚性问题, 它的经典Lipschitz常数可能很大, 但是它的单边Lipschitz常数很可能是适度大小的, 甚至是负的, 因此它能提供较好的逼真估计[4].

2 序列分裂方法

用序列分裂方法求解非线性自治常微分方程初值问题:

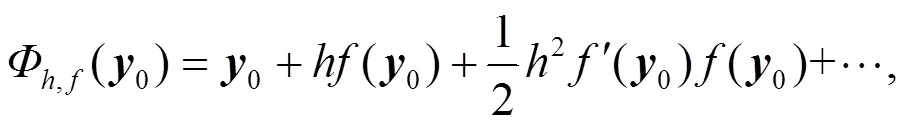
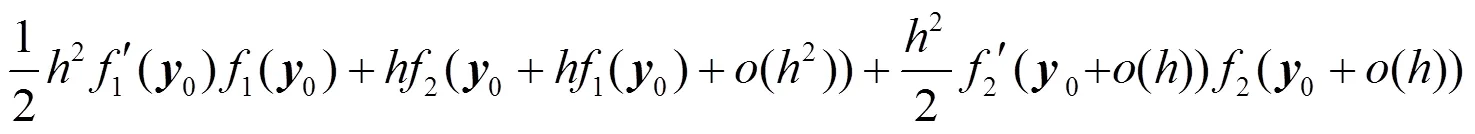
同样, 对非线性常微分方程情形, 序列分裂方法也具有一阶相容性.

针对问题(1)构造数值算法, 并研究其收敛性. 基于显式, 隐式Euler方法的序列分裂方法为:

3 数例

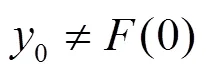
图1 h = 0.001数值解图像

图2 真解瞬变图像

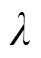
[1] 肖爱国, 李寿佛, 符鸿源,等. 非线性刚性微分方程算法理论的发展[J]. 自然科学进展, 1999, 9(增刊): 1183-1186.

[2] Dekker K, Verwer J G. Stability of Runge-Ktta methods for stiff nonlinear differential equations[M]. Amsterdam: North- Holland, 1984.

[3] Auzinger W, Frank R, Kirlinger G. Modern convergence theory for stiff inilial value problems[J]. J Comput Appl Math, 1993, 45: 5-16.

[4] Shampine L F, Gear C W. A user’s view of solving stiff ordinary differential equations[J]. SIAM Review, 1979, 21: 1-17.

Seriessplitting methods for solving a class of Stiff problems

LIU Guo-can

(Mathematics Department, Hunan University of Arts and Science, Changde 415000, China)

The series splitting methods was used to solve a class of stiff ordinary differential equation initial value problems. Theoritical analysis and numerical experiments show that series splitting methods were suitable for solving the class of stiff problems.

series stiff problems; splitting methods; consistency

O 241.8

1672-6146(2012)04-0001-03

10.3969/j.issn.1672-6146.2012.04.001

2012-10-16

刘国灿(1979-), 男, 讲师, 硕士, 研究方向为常微分方程的理论与应用. E-mail: lg3_527@126.com

(责任编校: 刘晓霞)