非守恒流体力学方程组粘性扰动技术的改进
张 瑗, 郭美珍
非守恒流体力学方程组粘性扰动技术的改进
张 瑗1, 郭美珍2
(1. 长沙理工大学 数学与计算科学学院, 湖南 长沙, 410004; 2. 湖南科技学院 计算机系, 湖南 永州, 425100)
结合以FD-WENO格式为基础构造的求解非守恒理想流体力学方程组的数值方法, 对求解非守恒流体力学方程组的粘性扰动技术进行了改进, 并通过求解Riemann问题对其进行了测试. 数值试验表明: 采用改进后的粘性校正项进行计算能够获得更好的数值结果.
双曲守恒律组; 非守恒方程组; 粘性扰动; FD-WENO格式
在绝热条件下, 守恒形式的一维可压缩理想流体力学方程组为:

其中,,分别表示流体的密度、速度和压强,表示单位质量流体所携带的总能量, 并设其满足气体状态方程:

这里是单位质量流体所携带的内能,是绝热指数, 对于空气=1.4. 令:

方程组(1)可表示为双曲守恒律组:

的形式, 并可用各种求解双曲守恒率组的数值格式, 如高阶FD-WENO格式[1]、Godunov格式[2]等进行求解. 然而在许多特殊情形下, 例如在可压缩多介质问题计算中避免压力振荡的需要以及对于某些特殊问题为了避免压强出现负值等, 我们选择通过关系式(2)把方程组(1)写成以内能作未知函数的非守恒形式:



直接离散非守恒系统会导致不正确的激波速度及通过激波传播的错误跳跃, 1992年, Karni于文献[3]中提出求解非守恒流体力学方程组(6)的粘性扰动技术, 在方程组的右端增加一个校正项, 再利用迎风格式进行求解, 非守恒系统理论及算法的更多研究可参见文献[4-5]. 我们也于文献[6]中以求解双曲守恒律组的5阶FD-WENO格式为基础, 结合粘性扰动技术构造了两类用于求解非守恒双曲型方程组的数值方法. 通过实践发现, 对于校正项的构造加以改进能够获得更好的计算效果.
1 粘性扰动技术的改进
以一维问题为例说明求解非守恒方程组(6)的粘性扰动技术及其改进.

对于文献[6]中构造的两类求解非守恒型方程组(6)的数值方法(方法1和方法2), 应用粘性扰动技术, 即在方程组右端增加一个校正项, 再用这两类数值方法进行求解, 如用方法1求解方程组:

其中,

这里1=|+|+|-|,2=|+|-|-|, 时间导数项用空间导数项代替, 即令:
u=-uu-(-1)()/,
其中空间导数项采用中心差商进行计算. 我们所采用的校正项类似于文献[3]是由一阶迎风格式推导出来的, 注意到方程组(5)中仅有第3个方程不守恒, 故式(9)中也只对第3个方程进行了修正. 通过实践我们发现, 它同样能与高精度格式较好地结合, 而且如果根据迎风效应改用向前或向后差商逼近和()能够获得更好的计算效果, 即可以改用式(10)计算式(9)中的空间导数项.

2 数值试验
通过数值试验对上述求解非守恒型方程组(6)的粘性扰动技术进行测试.

图1 Sod’s Riemann问题, 中心差商计算空间导数求解所获数值结果的密度值

图2 Sod’s Riemann问题, 改进式计算空间导数求解所获数值结果的密度值

图3 Lax’s Riemann问题, 中心差商计算空间导数求解所获数值结果的密度值
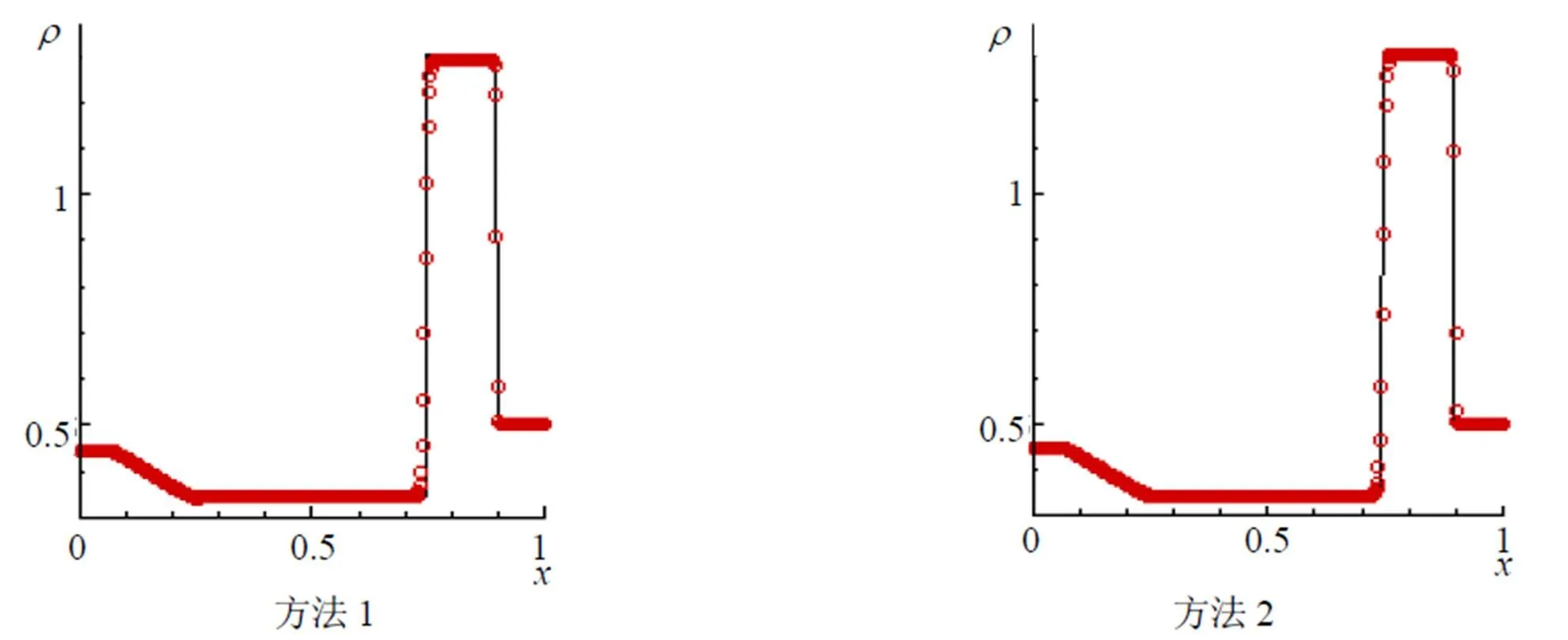
图4 Lax’s Riemann问题, 改进式计算空间导数求解所获数值结果的密度值
由算例1、2可看出采用方法1、2结合改进后的粘性扰动技术求解非守恒型方程组能够获得令人满意的数值结果, 特别是对于具有较强激波强度的Lax’s Riemann问题, 改进后的粘性扰动技术优势较为明显. 因此我们有理由相信, 采用非守恒形式求解较为复杂的流体力学问题时, 可以对其粘性校正项进行改进.
3 结论
本文对求解非守恒流体力学方程组的粘性扰动技术进行了改进, 数值试验表明: 在求解非守恒可压缩理想流体力学方程组时, 采用改进后的粘性校正项进行计算能够获得更好的数值结果. 但是也应当指出: 对于非守恒双曲型方程组(6)来说, 其理论与算法研究都绝非易事, 目前还没有相关理论表明其数值解一定能收敛到原问题的熵解. 因此我们建议在通常情况下, 应尽量将问题写成守恒形式进行求解, 只有在特殊情形下才考虑将问题写成非守恒形式进行求解.
[1] Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. J Comput Phys, 1996, 126(1): 202-228.
[2] 水鸿寿. 一维流体力学差分方法[M]. 北京: 国防工业出版社, 1998: 443-472.
[3] Karni S. Viscous shock profiles and primitive formulations [J]. SIAM J Numer Anal (S0036-1429), 1992, 29(6): 1592-1609.
[4] Castro M J, LeFloch P, Muñoz-Ruiz M L, et al. Why many theories of shock waves are necessary: Convergence error in formally path-consistent schemes[J]. J Comput Phys, 2008, 227(17): 8107-8129.
[5] Abgrall R, Karni S. A comment on the computation of non-conservative products[J]. J Comput Phys, 2010, 229(8): 2759-2763.
[6] 张瑗, 李寿佛. 非守恒理想流体力学方程组的若干数值方法[J]. 系统仿真学报, 2007, 19(17): 3914-3918.
The improvement of viscous perturbations technical fornon-conservative fluid dynamics equations
ZHANG Yuan1, GUO Mei-zhen2
(1. School of Mathematics and Computational Science, Changsha University of Science & Tecnology, Changsha 410004, China; 2. Department of Computer Science, Hunan University of Science and Engineering, Yongzhou 425100, China)
The improvement of viscous perturbations technical for non-conservative fluid dynamics equations has been put forward and were tested on Riemann problems conjunction with thenumerical methods based on FD-WENO schemes for solving non-conservative ideal fluid dynamics equations. The numerical evidence shows that the use of the improved viscous correction terms can get better numerical results.
hyperbolic conservation laws; non-conservative equations; viscous perturbation; FD-WENO schemes
10.3969/j.issn.1672-6146.2012.03.003
O 35; O 241.81
1672-6146(2012)03-0008-04
2012-06-25
湖南省教育厅科研项目(08C121); 湘潭大学“科学工程计算与数值仿真”湖南省重点实验室开放基金课题
张瑗(1978-), 女, 博士, 研究方向为计算流体力学及微分方程数值方法. E-mail: iamzhangyuan@163.com
(责任编校: 刘晓霞)

