采用标准尺的工作空间测量定位系统定向方法

杨凌辉，邾继贵，张广军，叶声华

(1. 北京航空航天大学精密光机电一体化技术教育部重点实验室，北京 100191；2. 天津大学精密测试技术及仪器国家重点实验室，天津 300072)

工作空间测量定位系统(workspace measurement positioning system，WMPS)是针对大型制造业测量需求特点而发展的一种新型多站网络式测量系统．系统由分布于工作空间内的多台激光发射站及位于待测点处的若干接收器组成，可同时对多个接收器进行跟踪定位，非常适于为工业机械手等自动化组装设备提供精确引导信息，近年来已成为国内外大尺寸测量领域研究的热点．目前产品化的WMPS系统只有Nikon Metrology生产的iGPS系统．在由4台发射站组成的测量网络中，iGPS坐标测量不确定度优于200,μm+10,μm/m，并已有英国巴斯大学及意大利都灵理工大学的研究人员对其进行性能评价验证[1-5]．在国内，除对 iGPS系统进行介绍外，西安交通大学刘志刚和天津大学邾继贵等[6-8]已分别研制出 N-RLATs(network of rotating laser automatic theodolites)系统及WMPS系统样机.

WMPS系统在工作时需要通过发射站定向得到发射站坐标系到全局坐标系的坐标变换关系(定向参数)，才能将各站坐标系统一到测量坐标系下并计算接收器坐标．在现有系统中，发射站定向通常采用接收器在测量空间内多个控制点处测量各站光信号并将控制点的坐标或相互距离作为已知条件建立优化方程，解算定向参数．控制点坐标值或距离值一般通过跟踪仪等辅助设备确定，如 iGPS系统在进行系统平差定向时需要用跟踪仪测量控制点间距离，而 NRLATs系统及WMPS系统需要采用位移平台或跟踪仪测量控制点坐标初值才能实现发射站定向[9-11]．

现有依靠辅助设备配合的定向方法虽然精度高，但是效率较低，定向过程中容易发生点位信息配对失误并导致解算失败，不适用于空间受限或需要快速组网测量的场合．为简化定向过程，提高测量效率，笔者在研究 WMPS系统测量原理的基础上，充分利用发射站工作时水平安置这一特点，引入2点距离约束结合发射站空间角度测量模型，提出采用标准尺的发射站全局定向方法，建立了基于几何约束的平差优化模型并给出了解算方法及初值生成方法．最后，采用天津大学测控国家重点实验室研制的WMPS系统对所述定向方法进行了验证．

1 WMPS系统测量原理及数学模型

1.1 发射站数学模型

WMPS系统组成如图 1所示．发射站工作时向测量空间内发射两束绕轴匀速旋转并带一定倾角的激光平面，同时每当平面转到预定位置处发射站发射光脉冲作为同步标记．当接收器收到发射站的旋转光平面信号或同步标记信号时，处理电路记录信号到达时间并将其转换为光平面旋转角度．计算机通过采集各个接收器记录的时间值可计算出此时接收器的精确坐标．

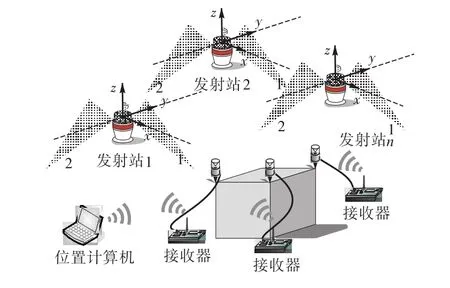
图1 WMPS系统组成示意Fig.1 Schematic configuration of workspace measurement positioning system

WMPS系统激光发射站可被抽象为绕公共转轴匀速旋转的 2个非平行半平面及 1个以固定频率发射脉冲光的点光源，其光平面结构参数及旋转角速度在制造时进行设定[8]．接收器则可简化为以靶面光学中心为中心的质点，数学模型如图2所示．

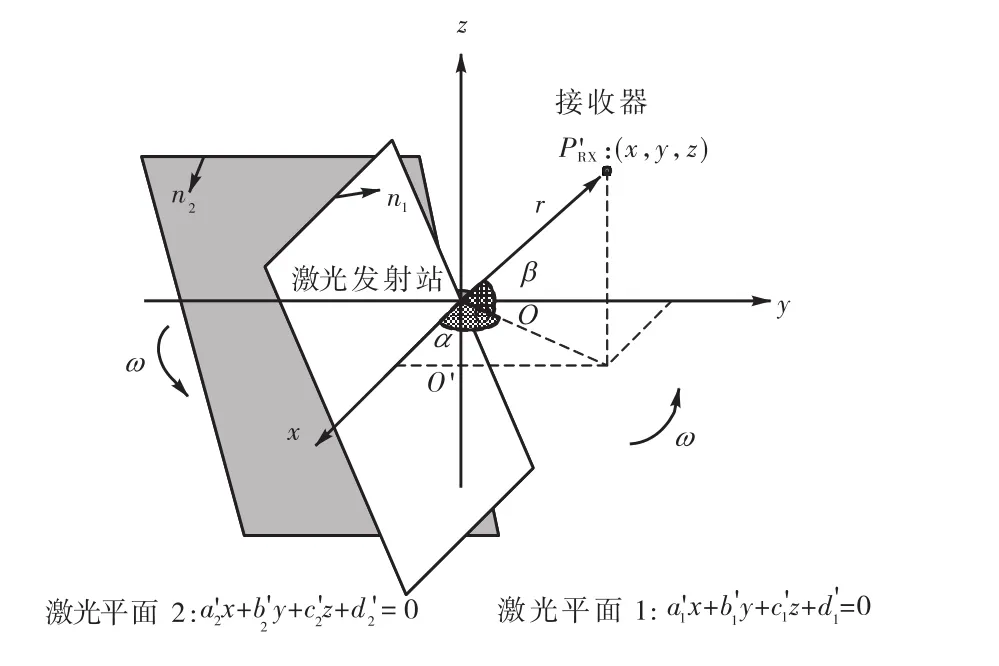
图2 数学模型Fig.2 Geometry model

定义激光平面1与转轴的交点O为发射站坐标系原点，2平面旋转轴为z轴，x轴为光平面转至固定位置，发射站发射脉冲光时(初始时刻)光平面1光轴所在位置，y轴遵循右手定则．如接收器在光平面内且在发射站坐标系下坐标为 P'RX：(x，y，z)T，则发射站的光平面与接收器位置关系可表示为

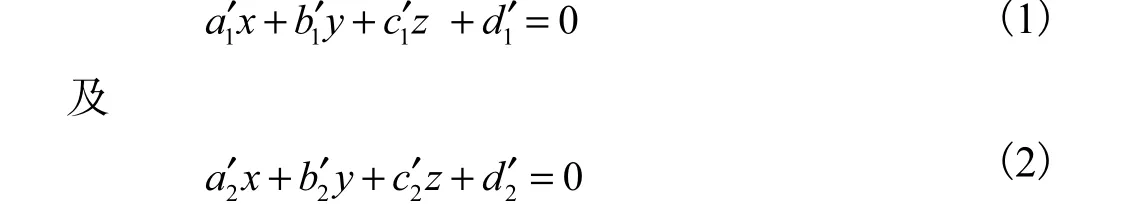
式中(a'1，b'1，c'1，d'1)T及(a'2，b'2，c'2，d'2)T为预先标定的光平面系数．当两平面激光分别扫过接收器时，测量同步光信号及扫描平面光信号到达光电二极管的时刻t0及t1、t2可得到光平面旋转角度为

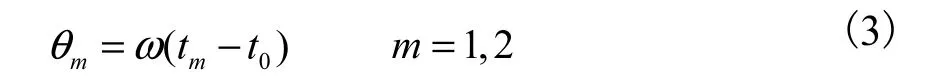
此时，在发射站坐标系下的平面方程系数变为旋转角度 θ1、θ2的函数为

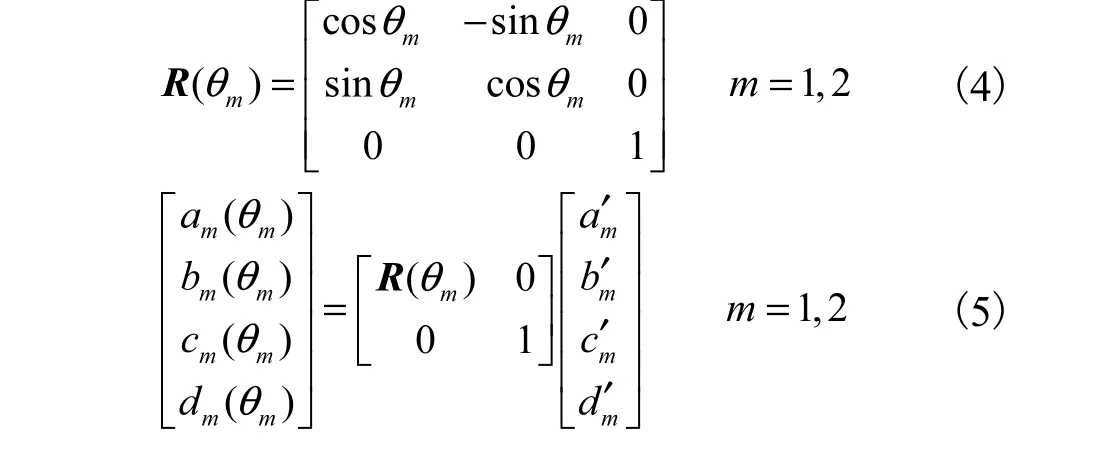
1.2 单站角度测量模型

由发射站数学模型可知当发射站的 2个扫描光分别到达接收器时，可求得光平面方程在发射站坐标系下的方程系数，则两平面法矢可表示为

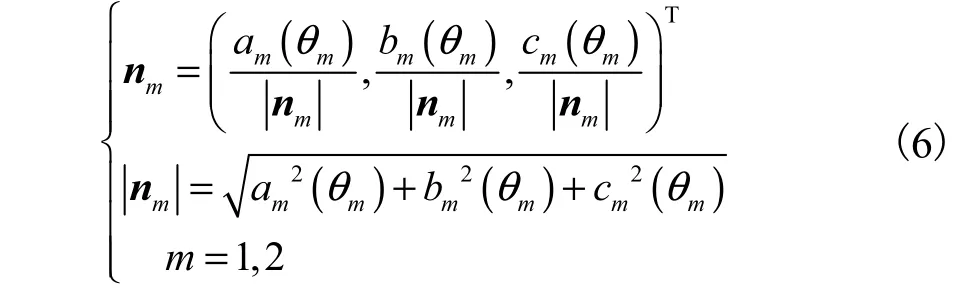
此时可由发射站原点引出一条射线指向接收器，并定义接收器在发射站坐标系下的俯仰角 β及方位角α，如图2所示．假设射线的方向矢量为r，则当接收器分别位于该发射站旋转激光平面 1及平面 2内时有1⊥rn，2⊥rn即制造过程中通常调整光平面 2与转轴交点近似与发射站原点重合，因此接收器在发射站坐标系下的方位角及俯仰角近似值为

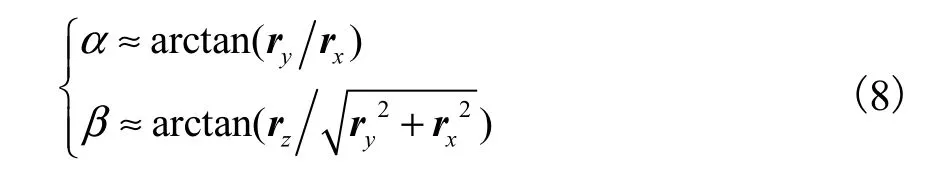
1.3 多站坐标测量模型

当系统定向完成后，发射站坐标系到测量坐标系的平移向量PTXG及旋转矩阵RTXG已知．如发射站的两扫描光平面分别到达待测接收器时，其转台转过角度分别为1nθ、2nθ，易知发射站在全局坐标系下光平面系数满足

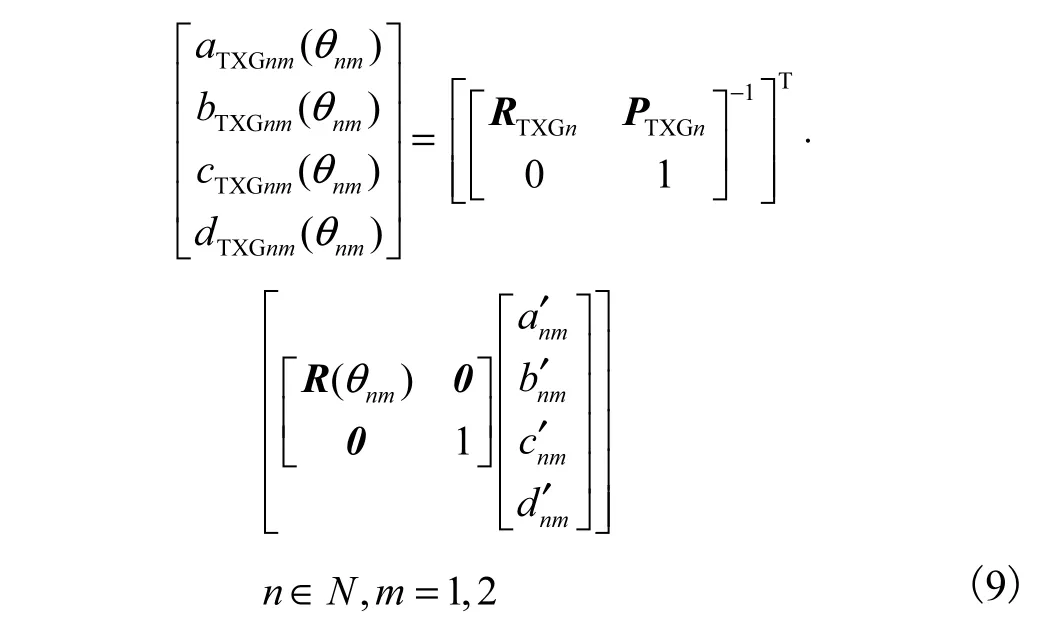
式中：m为发射站扫描光平面序号；n为发射站序号；TXG表示该参数为测量坐标系下的发射站结构参数．此时接收器在测量坐标系下坐标 PRXG：(xRXG，yRXG，zRXG)T待求，则有

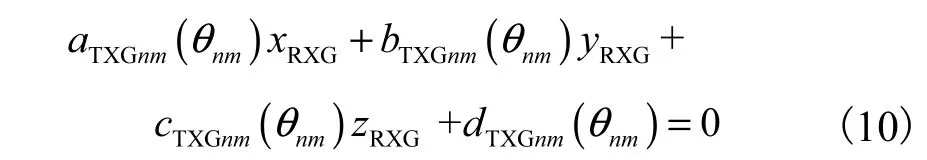
当测量空间内布置有 n台(n≥2)已定向发射站时可以列出 2n个形如式(10)的方程．对由这些方程组成的超定方程组进行最小二乘求解即可得到接收器坐标PRXG．

2 基于标准尺的定向算法

2.1 标准尺

WMPS系统所用标准尺由碳纤维或殷钢等温度系数较小的材料制成，同时尺两端各安装一个信号接收器，并配有信号处理单元，可独立采集两接收器数据，如图3所示．

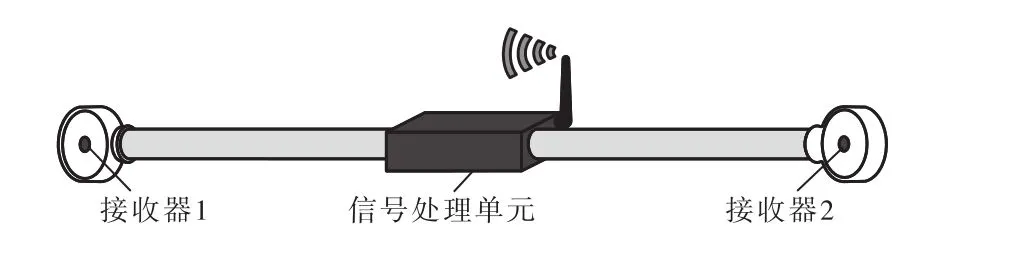
图3 标准尺Fig.3 Scale bar

可通过外部手段标定标准尺两接收器光学中心的准确距离，该数值即为标准尺长度，测量过程中可作为定值使用．

2.2 发射站定向模型

为便于分析WMPS系统发射站定向参数的解算过程，假设在标定时全局测量网络中包括 N台发射站，标准尺分布于 J个参考位置，并且接收器在每个参考点处都可接收到全部发射站发出的光信号．由坐标测量模型可知，当 2个光平面分别扫过接收器时，其测量坐标系平面方程系数可由式(9)得到．此时测量空间内任意一点坐标(x，y，z)到测站n的光平面m的距离约束dnm可以表示为

长期以来，测绘标准的制修订管理业务都是以电子文档、邮箱或电话方式进行交互式提交和反馈，标准制修订过程文档的存储由文件夹方式管理，导致标准制修订管理低效，资源共享性差，标准分析困难等。

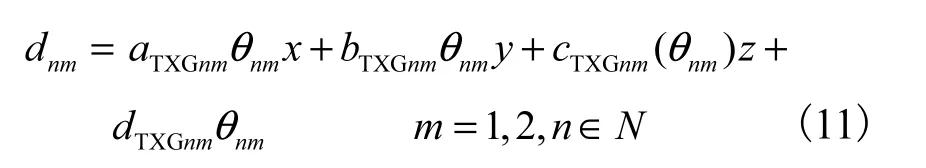
定向时，以 1号发射站坐标系为 WMPS系统测量坐标系，当采用4元数表示激光发射站坐标系到测量坐标系的旋转矩阵 RTXGn时，每个发射站有平移向量 PTXGn及旋转矩阵 RTXGn7个全局姿态参数未知数．如位置 j处的标准尺上接收器坐标：PRXGj1：(xRXGj1，yRXGj1，zRXGj1)T 及 PRXGj2：(xRXGj2，yRXGj2，zRXGj2)T未知，则每处标准尺引入6个未知数，总未知数为 7(N-1)+6,J，如果每个参考位置处的接收器都可以接收到全部发射站发出的光信号，则可以列出4,NJ个形如下式

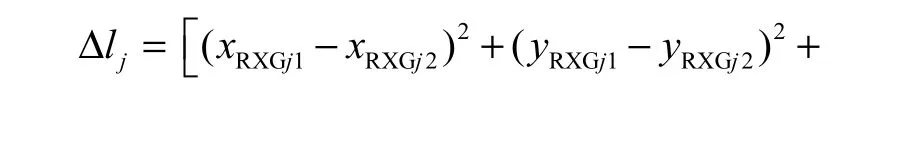
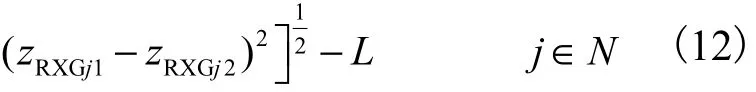
的优化方程．考虑标准尺两端的接收器及标准尺本身长度还可构造约束关系．则此时约束方程总数为4,NJ+J．当 4,NJ+J＞7,N+3,J，通过式(11)及式(12)可以构造目标函数为

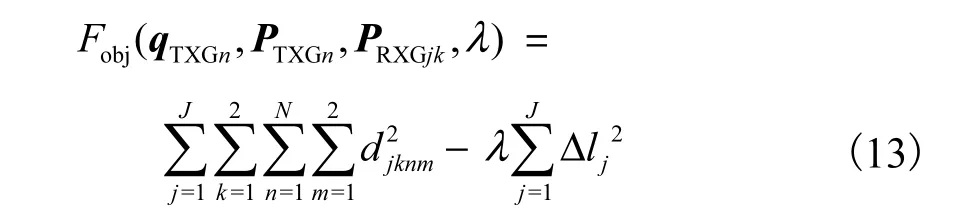
采用 L-M 算法对该目标函数进行最小二乘优化求解即可得到每个发射站在测量坐标系下的定向参数最优解[12]．

2.3 迭代初值生成

对式(13)进行优化求解的关键前提是以标准尺两端接收器的坐标近似值作为迭代初值．由于WMPS系统工作时发射站通常采取水平安置的方式，因此当标准尺竖直放置时靠发射站测角功能结合三角关系即可估算标尺两端接收器在各站坐标系下的坐标近似值．此时，标准尺方向与发射站转轴近似平行，采用接收器角度测量式(8)可分别得到标准尺顶部接收器的俯仰角β1及水平角α1，以及底部接收器的俯仰角β2及水平角α2，如图4所示．

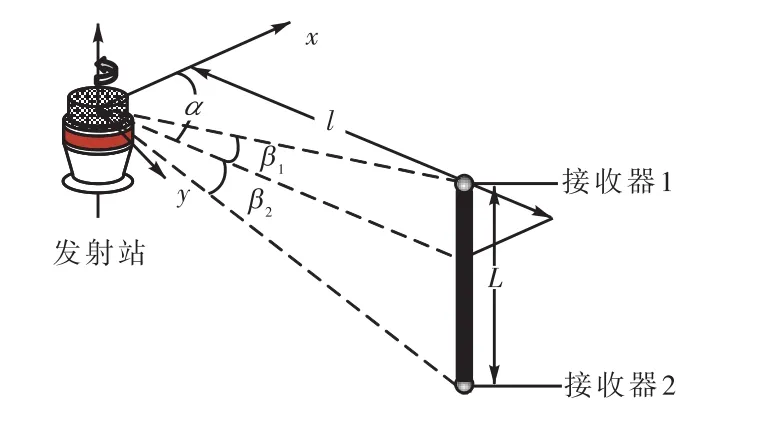
图4 坐标估算Fig.4 Coordinate estimation

如已知标准尺长 L，则标尺到发射站的水平距离l近似为

当得到多个位置处标准尺两端接收器在不同发射站下的坐标近似值后，可采用基于刚体运动学的坐标系配准算法求解测量网络内其他发射站到 1号发射站的旋转矩阵及平移向量初值[13]．将这些迭代初值连同标准尺长度约束带入优化方程(12)进行优化求解便可得到精确坐标转换关系．

3 实验验证

图5 实验环境Fig.5 Experimental environment

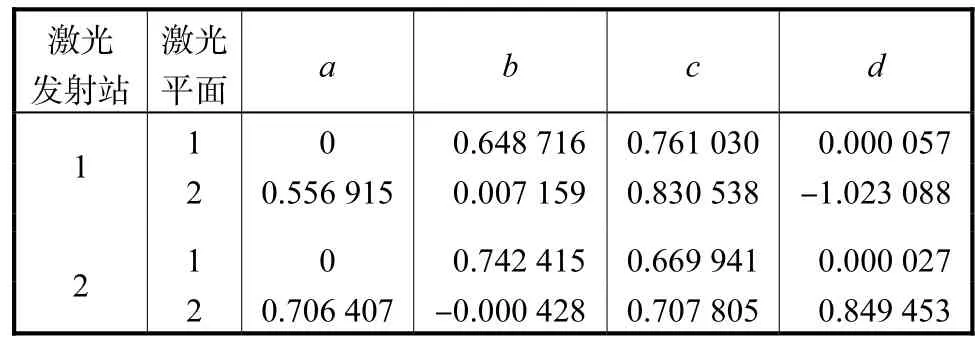
表1 发射站光平面参数Tab.1 Optical plane’s parameters of transmitters

由求解条件可知，标准尺最少移动4次即可完成双站系统定向．因此，定向过程中首先采用标准尺在距两发射站约6,m远处3.5,m×4.0,m×2.0,m的空间内分别移动4次，解算后得到的发射站2个定向参数(单位：mm)结果为

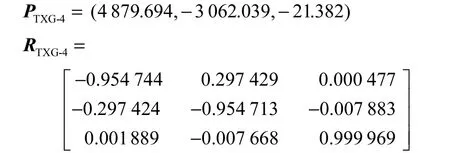
为考察参与标定的标准尺位数量对定向精度的影响，在保持发射站不动的前提下，增加测量空间中用于标定的标准尺参考位置并进行重新标定．当标准尺参考位置增加至8个时，解算得到的发射站两定向参数(单位：mm)结果为

当标准尺参考位置增加至 16个时，得到的发射站两定向参数(单位：mm)结果为

上述 3组标定结果说明当采用最小二乘优化求解发射站两定向参数时，解算结果随标定参考位置不同而略有不同，但随位置数量的增加而趋于稳定．为验证不同情况下的定向精度，采用同一标准尺在标定空间内不同位置进行了 10次验证测量，并采用上述3组定向参数分别解算了10个位置标准尺长度l，如图6所示．

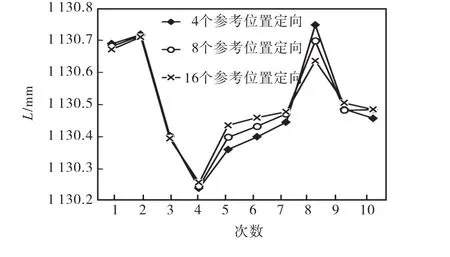
图6 采用不同定向参数的标准尺长度测量结果Fig.6 Scale bar length measurement results using different orientation parameters

由图6中3组验证结果对比可知，标准尺长度测量误差随标定参考位置的增加而趋于减小，即增加标定参考位置的数量可在一定程度上提高标定精度．其中采用 16个参考位置定向结果解算得到的接收器坐标及尺长测量误差Δl如表2所示.

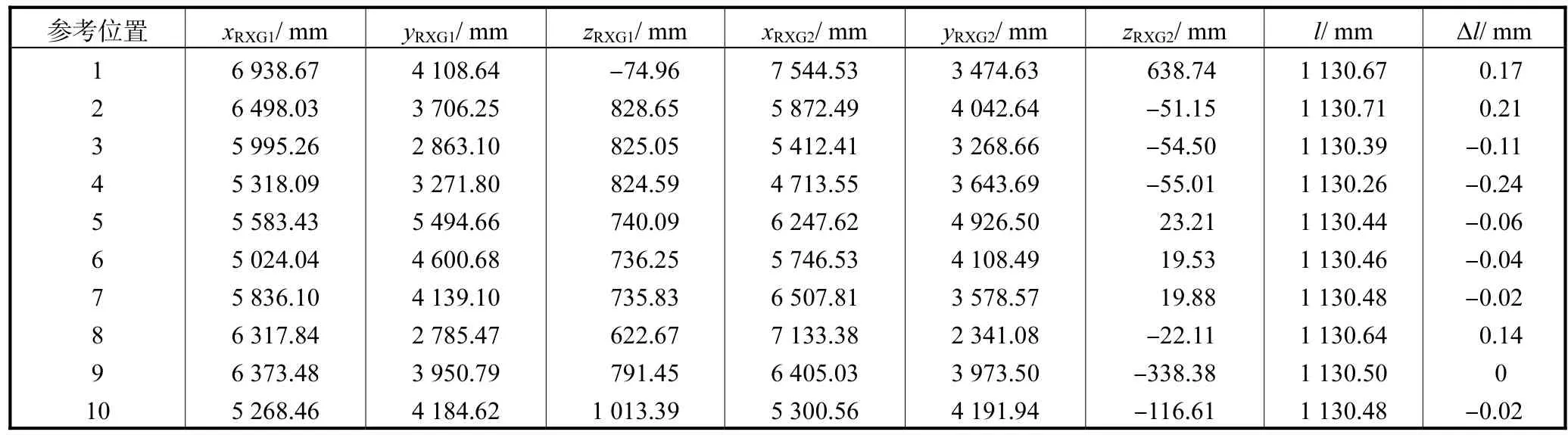
表2 标准尺接收器坐标及长度测量结果Tab.2 Scale bar’s reciever coordinates and length measurement results

由以上实验结果可知，当采用 16个参考位置定向时尺长测量误差可控制在 0.25,mm以内．由于现有测量原理默认发射站工作时保持匀速旋转，因此测量时接收器坐标测量精度及标准尺长度测量精度主要受到发射站转速控制稳定性的影响．另一方面，受到器件制造工艺(感光元件外形及封装厚度)限制，尺上接收器在接收不同方向光信号时也会引入角度测量误差．因此，在采用竖直姿态标准尺生成迭代初值进行定向优化求解后，竖直状态下的尺长验证测量精度略高于其他姿态．

4 结 论

(1) 在介绍了工作空间坐标测量定位系统的基础上建立了基于光平面方程描述的发射站数学模型，并推导了接收器角度测量公式及坐标测量方程．

(2) 利用发射站工作时水平安置这一特点，引入2点距离约束结合发射站空间角度测量模型，提出了采用标准尺的发射站全局定向方法，建立了基于几何约束的平差优化模型，最后通过实验对所述定向方法进行了验证．

(3) 以含有2台激光发射站的WMPS测量系统为基础，通过实验验证了所述系统定向方法及优化模型，定向过程中标准尺长度解算误差小于 0.25,mm，已达到国外同类设备水平．

(4) 相比于现有采用辅助设备的定向方法，新方法在保证测量精度的前提下使测量效率大大提高．通过改善器件加工精度、提高发射站稳速精度及适当增加参考点位，系统标定精度具有进一步提高的空间，在大尺寸测量中具有广泛的应用前景．

［1］ Nikon Metrology，iSpace Large Volume Metrology，Tracking and Positioning [EB/OL]. http：//www. nikonmetrology. com/en_EU/Literature-Downloads，2012.

［2］ Cuyper W，Van Gestel N，Voet A，et al. Optical measurement techniques for mobile and large-scale dimensional metrology [J].Optics and Laser in Engineering，2009，47(3/4)：292-300．

［3］ Muelaner J E，Maropoulos P. Large scale metrology in aerospace assembly[C]// 5,th International Conference on Digital Enterprise Technology. Nantes，France，2008：22-24.

［4］ Maisano D A，Jamshidi J，Franceschini F，et al. Indoor GPS：System functionality and initial performance evaluation [J].International Journal of Manufacturing Research，2008，3(3)：335-349.

［5］ Muelaner J E，Wang Z，Jamshidi J，et al. Study of the uncertainty of angle measurement for a rotary-laser automatic theodolite(R-LAT)[J].Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，2009，223(B3)：217-229.

［6］ Liu Zhigang，Xu Yaozhong，Liu Zhongzheng，et al. A large scale 3D positioning method based on a network of rotating laser automatic theodolites [C]//Proceedings of the2010IEEE International Conference on Information and Automation. Harbin，China，2010：513-518.

［7］ Yang Linghui，Yang Xueyou，Zhu Jigui，et al. A novel method for spatial angle measurement based on rotating planar laser beams [J].Chinese Journal of Mechanical Engineering，2010，23(6)：758-764.

［8］ 劳达宝，杨学友，邾继贵，等. 扫描平面激光空间定位系统测量网络的构建[J]. 光电子·激光，2011，22(2)：261-265.

Lao Dabao，Yang Xueyou，Zhu Jigui，et al. Constructing measuring network with scanning planar laser space position system[J].Journal of Optoelectronics·Laser，2011，22(2)：261-265(in Chinese).

［9］ Muelaner J E，Wang Z，Martin O，et al. Verification of the indoor GPS system by comparison with points calibrated using a network of laser tracker measurements[C]//Proceedings of the6,th CIRP-Sponsored International Conference on Digital Enterprise Technology.Hong Kong，China，2009：607-619.

［10］ 刘志刚，许耀中，王民刚，等. 基于双旋转激光平面发射机网络的空间定位方法：中国 101329165[P].2008-12-24.

Liu Zhigang，Xu Yaozhong，Wang Mingang，et al．Space Positioning Method Based on Double-Rotating Laser Plane Transmitter Network：CN 101329165[P].2008-12-24(in Chinese).

［11］ 杨凌辉，杨学友，劳达宝，等. 采用光平面交汇的大尺寸坐标测量方法[J]. 红外与激光工程，2010，39(6)：1105-1109.

Yang Linghui，Yang Xueyou，Lao Dabao，et al.Large-scale coordinates measurement method based on intersection of optical planes [J].Infrared and Laser Engineering，2010，39(6)：1105-1109(in Chinese).

［12］ Madsen K，Nielsen H B，Tingleff O. Methods for Non-Linear Least Squares Problems [EB/OL]. http：//citeseerx. ist. psu. edu/viewdoc/summary?doi＝10. 1. 1. 73.3864，1999.

［13］ 耿 娜，邾继贵，劳达宝，等. 基于刚体运动学的坐标系配准理论及算法[J]. 传感技术学报，2010，23(8)：1088-1092.

Geng Na，Zhu Jigui，Lao Dabao，et al. Theory and algorithm of coordinate system registration based on rigid body kinematics[J].Chinese Journal of Sensors and Actuators，2010，23(8)：1088-1092(in Chinese).