船舶与桥梁结构防撞消能器碰撞非线性有限元数值仿真研究

伍建强,丁 青,李德慧,邓 磊

(江西省交通科学研究院,南昌 330038)

船舶与桥梁结构防撞消能器碰撞非线性有限元数值仿真研究

伍建强,丁 青,李德慧,邓 磊

(江西省交通科学研究院,南昌 330038)

船桥碰撞是在巨大碰撞荷载作用下的一种复杂的非线性动态响应过程。非线性有限元技术能够较好地解决船桥碰撞问题。简述该技术的基本原理,以碰撞仿真的基本理论为基础,数值仿真模拟船舶与桥梁结构防撞消能器进行正向碰撞过程,并对碰撞过程中的碰撞力演化、能量转化和防撞消能器的塑性变形的整个时间历程进行详细描述和全面细致的仿真模拟。非线性有限元技术比传统的准静态理论提供更为精确的结果。所提供的防撞消能器的塑性变形(即撞击深度)对设计有重要参考价值。

船桥碰撞;非线性有限元;防撞消能器;塑性变形

随着交通运输事业的不断发展,船舶、汽车和火车交通量增大,因受船舶撞击而诱发的桥梁垮塌事件正在日益增多。资料统计表明,最近10余年来,世界上发生的船舶撞墩毁桥的重大事故就已超过100余起,图1列出了桥梁结构撞毁事件的几个例子。这类事件往往造成桥塌、船沉、人亡和水陆运输干线长期中断的严重后果。重建桥梁和疏通航道的费用十分惊人。因此,预防桥梁免遭船舶撞击这一问题已成为具有广泛意义的国际性课题,日益引起各国政府、学者和工程界的关注[1,2]。

图1 桥梁结构撞毁事件

Minorsky理论[3]、汉斯-德鲁彻理论[4]和简化解析法[5]是现今分析船桥碰撞问题常用方法的基础,可上述理论均基于准静态的模拟分析碰撞。然而,船桥碰撞是桥梁结构和船体结构在很短时间内在巨大冲击荷载作用下的一种复杂的非线性动态响应过程,它具有非常明显的动力特征,而且碰撞区构件一般都要迅速超越弹性阶段而进入塑性阶段,并可能出现撕裂、屈曲等各种形式的破坏,所以以现有的船桥碰撞理论来分析船桥碰撞是不够准确的。

随着非线性有限元技术的日益进步和成熟,被广泛地应用于结构冲击数值模拟计算中,使有限元数值仿真技术能够较好地解决船桥碰撞问题。Gary R. Consolazio等人利用非线性有限元程序对船舶和圆形、方形桥墩碰撞进行了研究[6];刘建成、顾永宁对整船整桥模型的船桥碰撞进行过数值仿真分析[7];高震、顾永宁利用超大型油船船侧结构碰撞大尺度模型试验的测量结果验证非线性有限元方法的计算结果的可信性和精度[8]。

本文以碰撞仿真的基本理论和关键技术为基础,数值模拟船舶对某大桥主桥桥墩的防撞消能器进行正向碰撞过程分析,并对碰撞过程中的碰撞力演化、碰撞能量转化以及防撞消能器的防撞能力(即最大吸收能量)进行了描述和力学机理分析,研究碰撞现象内在的规律性,表明了碰撞数值仿真分析应用的优势和前景。

1 非线性有限元动态数值仿真理论

1.1 非线性有限元控制方程

船桥碰撞问题的运动方程可以一般地表示为

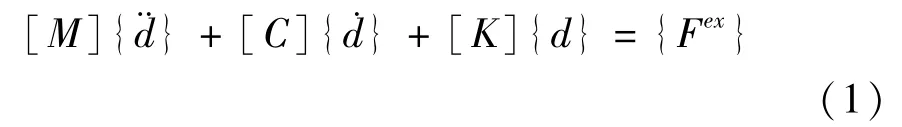
式中,[M]为船桥质量矩阵;[C]为阻尼矩阵; [K]为刚度矩阵;{¨d}为加速度向量;{˙d}为速度向量; {d}为位移向量;{Fex}为外力向量。碰撞力通过定义船舶/防撞系统之间为接触面以接触力的形式输出。

经有限元离散处理后形成的瞬态动力学问题,适宜采用显示直接时域积分解法。通过自动控制时间步长,可以得到稳定解并保证时间积分的精度。实用中以最小有限单元网格的特征长度除以应力波速来定义最小时间步长[9],即

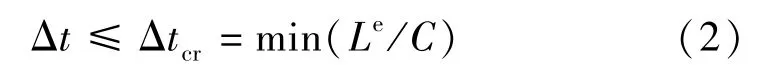
1.2 碰撞中的接触算法[7]

相撞结构(或构件)之间的相互作用通过接触算法来完成。在可能发生接触作用的两个结构表面之间分别定义主从接触面,参见图2。在求解的每一时间步,检查从属节点是否已经穿透主面,如果还没有穿透,则计算工作继续进行;否则在垂直于主面的方向上施加一作用力以阻止从属节点的进一步穿透,这个作用力就是接触力。

本文计算借助了功能较强的非线性有限元软件LS-DYNA程序完成。

图2 主从接触面

2 船舶与防撞消能器碰撞仿真计算模型

2.1 工程概况

某大桥为一PC连续刚构桥,主墩为双薄壁型墩,基础承台尺寸为18.6m×12.6m×5m。设计要求通航满载1 000 t的船舶。该桥的主墩上设置角钢支承钢管架形式的防撞消能器,详见图3。该防撞消能器的尺寸参考文献[10]取用。其材料采用Q235钢,钢管直径为800 mm,厚度为10 mm,支架角钢型号为100mm×100 mm×10 mm,节点钢板厚度除1～6为20mm外,其余均为10mm。

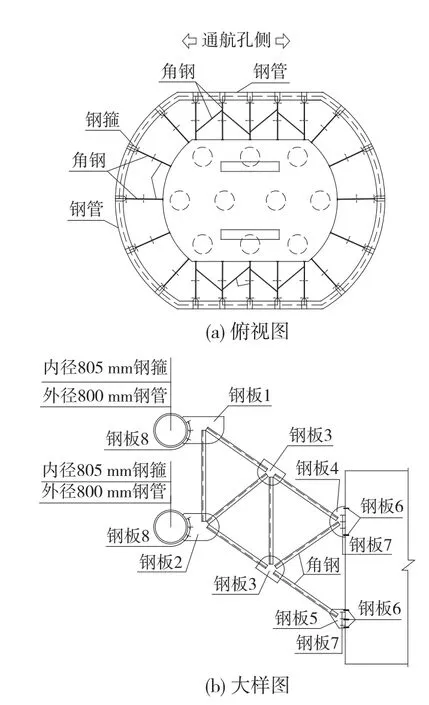
图3 防撞消能器尺寸构造

2.2 材料的应变率敏感性分析[11]

现今大部分桥梁的防撞装置均采用低碳钢制造,钢材料的塑性性能对应变率是高度敏感的,它的屈服强度随应变率的增加而提高。因此,在材料模型中应计入应变率敏感性的影响,以考虑碰撞问题的动力特征。在材料应变率敏感性诸多的本构方程中,与实验数据符合较好的Cowper-Symonds本构方程

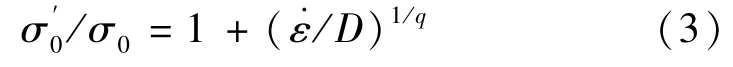
式中,σ′0为在塑性应变率 ˙ε时的动屈服应力;σ0为相应的静屈服应力;D、q为材料的应变率参数。对低碳钢,D=40.4,q=5。

针对防撞装置用钢,考虑等向强化和随动强化对材料的贡献,需要计入强化参数β。随动强化时β=0,等向强化时β=1。所以在分析船舶碰撞桥梁问题中防撞装置采用改进的Cowper-Symonds本构方程

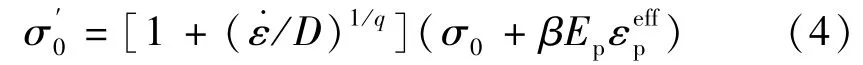
式中,Ep为塑性强化模量;εeffp为有效塑性应变。

2.3 数值仿真分析的有限元模型建立

船舶与桥梁结构的碰撞过程十分复杂,其与碰撞时的环境因素(风浪、气候、水流等)、船舶特性(船舶类型、船舶尺寸、行进速度、装载情况以及船首、船壳和甲板室的强度和刚度等)、桥梁结构因素(桥梁构件的尺寸、形状、材料、质量和抗力特性等)及驾驶员的反应时间等因素有关。由于船桥碰撞过程的复杂性,在数值仿真分析中对其进行简化是十分必要的,在研究船桥碰撞时,船舶的动能、船桥之间的接触和桥梁结构形式是主要因素[6]。

研究桥梁结构防撞消能器的防撞消能效果关键是要获得船桥之间的撞击力及撞击过程中防撞消能器吸收能量的情况。因此,在研究船舶碰撞防撞消能器时只对防撞消能器建立有限元模型,由于桥梁上部、下部结构的动力响应对能量的迁移吸收影响很小,可以将其忽略。

船体周围水介质伴随船体运动并参与碰撞能量吸收,由于船舶与防撞结构发生碰撞时,碰撞中船体主要在纵向上发生刚性位移,此时其周围水介质的影响相对较小,采用大小为船体总质量的0.04倍的附加水质量就可以相当准确地表达水的影响[12]。

在研究船舶与防撞结构碰撞时,数值仿真中建立一个有效的有限元模型至关重要。在建立防撞结构有限元模型时,由于角钢与角钢之间和角钢与钢管之间的节点钢板比较刚硬,在有限元模型中采用刚结点处理,角钢支架与基础承台连接处采用固定支座;由于碰撞过程中主要研究防撞消能器的变形吸能能力, DYNA程序中采用梁单元来模拟钢管和角钢支架是合理的[10],钢管梁单元和角钢梁单元的截面分别为空心钢管截面和角钢截面,防撞消能器的有限元模型如图4(a)所示。

船舶碰撞防撞结构时,碰撞过程中的能量主要来自于船舶的动能,碰撞结束后,除防撞消能器吸收大部分能量外,船体也会发生一些变形以吸收部分能量。在建立船舶有限元模型时,为了模拟船体碰撞时的变形,在船舶与防撞结构碰撞的接触部分(即船首)采用壳单元,即THIN SHELL163单元,船体采用实体单元建立以代替船舶的实际质量(包括附加水质量),保证碰撞过程中的船舶动能与实际一致,船舶发生的变形主要通过船首的壳单元变形来体现,船舶的结构形式和尺寸参考文献[6],其有限元模型如图4(b)所示。

基于上述讨论,利用LS-DYNA非线性有限元程序对某大桥的防撞消能器及船舶建立有限元模型,对船舶与防撞消能器正向碰撞过程进行了数值仿真模拟,并对碰撞过程中防撞消能器的动力性能进行了研究。数值仿真分析中采用梁单元(BEAM161)来模拟防撞结构,船舶采用壳单元(SHELL163)和实体单元(SOLID164)2种,整个有限元模型中,梁单元共16 240个,壳单元25 000个,实体单元500个。

图4 仿真计算有限元模型

对船用低碳钢和防撞结构低碳钢,在碰撞过程中材料已经进入非线性阶段。低碳钢材料采用双线性强化弹塑性本构关系,并且材料属性全部采用改进后的Cowper-Symonds本构方程。材料中仅考虑随动强化对低碳钢的贡献,计算模型中各参数取值如下:材料密度ρ=7.85×103kg/m3,弹性模量E=2.1×1011N/m2,硬化模量Eh=1.18×109N/m2,屈服应力 σ0=2.35×108N/m2,泊松比v=0.3,应变率参数D=40.4,应变率参数q=5,强化参数 β=0,最大失效等效应变 εfailure=0.34。

3 数值仿真计算结果及其分析

3.1 船舶与防撞结构之间的碰撞力分析

船舶与防撞结构之间的碰撞力是指它们碰撞时之间的相互作用力(即两者之间的接触力),碰撞力的大小表征着船舶对防撞结构的破坏程度。图5显示的是1 000 t船舶以3m/s速度对防撞消能器进行正向碰撞过程中,船舶与防撞结构之间的碰撞力的时程曲线。从图中可以看出,碰撞力曲线具有非线性波动特征。在碰撞过程的不同阶段,碰撞力出现不同程度的跳跃现象,每一次碰撞力的跳跃提高表示了应力波的传播使防撞结构中的某部分构件有效地参与到防撞工作中;每一次碰撞力的跳跃降低表示了某部分构件的失效或破坏。本例中碰撞力的下降主要是由部分角钢支承骨架结构发生动态屈曲造成的。

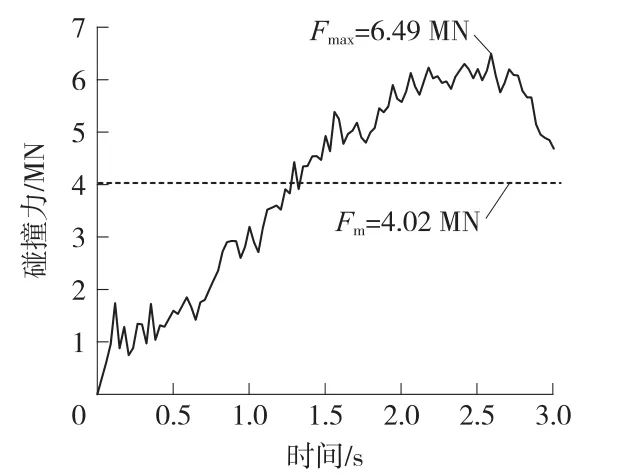
图5 碰撞力的时程曲线

图5中Fmax=6.49 MN表示碰撞过程中的最大碰撞力,Fm=4.02 MN表示碰撞过程中的平均碰撞力。从图中可以看出,开始时碰撞力随着时间增加(即撞击深度的增加)逐渐增大,当最大碰撞力出现后,碰撞力曲线开始下滑(即碰撞力曲线最后一段),这是由于船舶撞击防撞结构后反弹的原因,上述计算结果与文献[6,7]的研究结果基本上是一致的。

表1列出了1 000 t和3 000 t船舶分别以1、3、5m/s的速度对防撞消能器正向碰撞的碰撞力。碰撞过程中,尽管最大碰撞力很大,但由于其持续时间极短,对结构物的破坏作用十分有限,因此,主要通过平均碰撞力的大小来判定船舶对桥梁结构防撞消能器撞击的损坏程度,也即碰撞过程中的平均碰撞力越大,防撞消能器被撞损的程度越大。从表中可以看出,随着船舶的初始动能增加,平均碰撞力也在随之增大,由此可以得出,船舶的动能越大,平均碰撞力越大,对防撞消能器撞击的损坏程度越大。从平均碰撞力与最大碰撞力的比值不难发现,平均碰撞力约为最大碰撞力的一半,这与1976年德国沃辛实验结果表明的最大碰撞力约为平均碰撞力的2倍的结论是相当吻合的[13]。

3.2 碰撞过程中的能量转化

在碰撞过程中,船舶的初始撞击动能(包括附加水质量提供的动能)将转化为如下几种能量:撞击船的弹塑性变形能及剩余动能;防撞结构的弹塑性变形能及动能;构件之间摩擦引起的热能损伤。此外DYNA程序中体单元和壳单元只有一个积分点(位于单元形心处),单元的某些变形模态不具有刚度,从而造成了沙漏现象,并引起一定的能量损失,通过采用添加黏性阻尼系数以及合理划分网格的方法,可以将沙漏引起的能量损失控制在一个很小量,关于沙漏现象的详细论述参见文献[9]。计算结果表明,在上述能量中摩擦引起的能量损失很小。因此,船舶的初始动能主要转化为防撞结构的变形能及动能、撞击船的变形能及剩余动能。

图6为1000t船舶以3m/s速度对防撞消能系统进行正碰撞过程中的能量转化及能量时程曲线。A线代表整个系统的总能量,B线和C线分别代表整个系统的动能和变形能(整个系统的动能和变形能包括防撞结构和船舶两者)。从图中可以看出,整个系统的动能(B线)逐渐减小,同时整个系统的变形能(C线)逐渐增加,即系统动能已经转化成为系统变形能,但整个系统的总能量(A线)保持不变(A线为一水平线),这正好说明了碰撞过程中能量转化是满足能量守恒定律的。

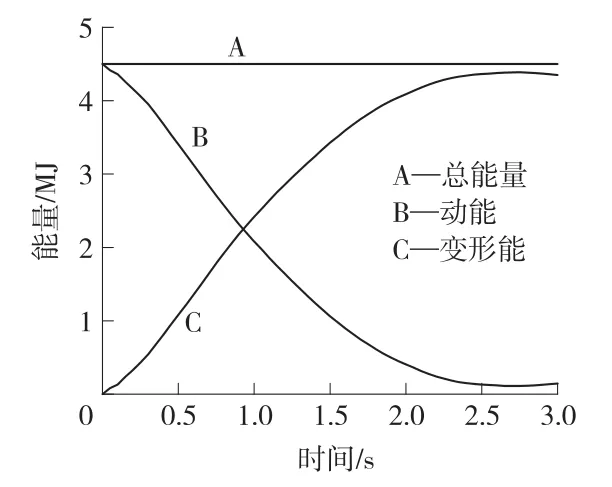
图6 能量时程曲线

3.3 防撞消能器的损伤变形分析

在不同初始动能的船舶撞击下,桥墩的防撞消能器的塑性变形的大小是不相同的,当其塑性变形大于安全设计距离(即最大允许撞击深度),防撞消能器就会失效,船舶将直接撞击桥墩。因此,数值仿真分析中,规定当船舶直接碰撞并接触桥墩表面时,防撞消能器将退出防护的工作状态。防撞消能器的最大允许撞击深度为4.3m。

图7显示的是1 000 t船舶以3m/s速度对防撞消能器进行正向碰撞过程中它的损伤变形历程,撞击深度1.46m。从图中可以看出,当船舶撞击防撞消能器时,防撞消能器除了发生整体变形外,其塑性变形主要在船舶撞击附近处较大,显示出较强的局部性。

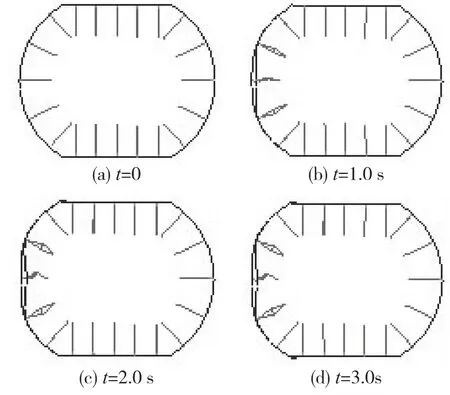
图7 防撞消能器的损伤变形历程

表2列出了1 000 t和3 000 t船舶分别以1、3、5m/s的速度对防撞消能器正向碰撞下它的变形能以及撞击深度。从表中可以看出,当船舶撞击防撞消能器时,耗散动能大部分转化为防撞消能器的变形能(即被防撞结构所吸收),随着船舶的初始动能增加,防撞消能器的撞击深度也在增大。当质量为1 000 t的船舶以1、3、5m/s的速度对防撞消能器正向碰撞时,撞击深度分别为0.23、1.46、3.95 m,均小于最大允许撞击深度4.3m,防撞消能器对桥墩仍处于防护工作状态。当质量为3 000 t的船舶以3、5m/s的速度对防撞消能器正向碰撞时,撞击深度超出最大允许撞击深度,防撞消能器已经失效,船舶将直接撞击桥墩。从表中不难发现,对于防撞消能器而言,它的防撞能力(即最大吸收能量)只与自身结构和材料的性质有关,而与撞击船舶的初始动能无关。

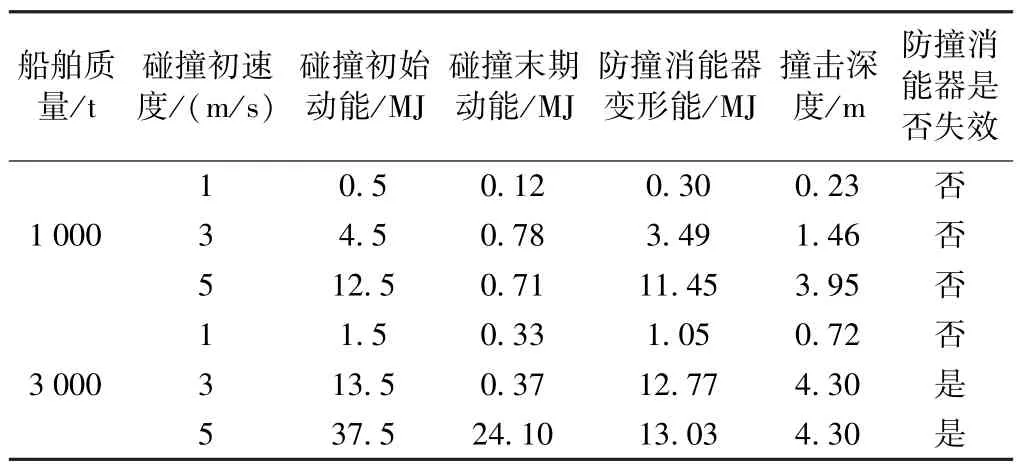
表2 不同初始动能的船舶正向碰撞下防撞消能器的变形能以及撞击深度

4 结论

(1)采用显式瞬态非线性有限元分析技术可以对船舶与桥梁结构防撞消能器碰撞过程进行成功的数值仿真分析。数值仿真分析结果可以反映出碰撞过程中的一般现象和基本规律,可以比较精细地再现结构内部的动力学过程,并对船舶与防撞消能器碰撞过程中的碰撞力演化、能量转化和防撞结构的塑性变形的整个时间历程进行全面细致的模拟再现。

(2)在船舶撞击防撞结构的过程中,由于防撞结构中的某些构件不断的失效和破坏,碰撞力曲线呈现出非线性波动特征。碰撞力随着时间增加(即撞击深度的增加)逐渐增大,当最大碰撞力出现后,碰撞力曲线开始下滑(即碰撞力曲线最后一段),这是由于船舶撞击防撞结构后反弹的原因。平均碰撞力的大小可以用来衡量船舶对桥梁结构防撞消能器撞击的损坏程度,船舶的初始动能越大,平均碰撞力越大,船舶对防撞消能器撞击的损坏程度越大。平均碰撞力约为最大碰撞力的一半,与德国沃辛实验结果吻合。

(3)在能量方面,船舶的耗散动能大部分转化为防撞消能器的变形能(即被防撞结构所吸收),同时,整个系统的总能量却保持不变,说明碰撞过程中能量转化是满足能量守恒定律的。

(4)当船舶撞击防撞结构时,防撞结构除了发生整体变形外,其塑性变形主要在船舶撞击附近处较大,显示出较强的局部性。船舶的初始动能越大,防撞消能器的撞击深度越大。当质量为1 000 t的船舶以1、3、5m/s的速度对防撞结构进行正向碰撞时,撞击深度分别为0.23、1.46、3.95m,均小于最大允许撞击深度4.3m,防撞消能器对桥墩仍处于防护工作状态。当质量为3 000 t的船舶以3、5m/s的速度对防撞结构进行正向碰撞时,撞击深度超出最大允许撞击深度,防撞消能器已经失效,船舶将直接撞击桥墩。

(5)对于防撞消能器而言,它的防撞能力(即最大吸收能量)只与自身结构和材料的性质有关,而与撞击船舶的初始动能无关。

[1] 杨渡军.桥梁的防撞保护系统及其设计[M].北京:人民交通出版社,1990.

[2] Risk to historical bridges due to ship impact on German inland waterways[J].Reliability Engineering and System Safety,2005(90): 261 -270.

[3] V U Minorsky.An analysis of ship collision to protection of nuclear powered plant[J].Ship Research,1959(1):1 -4.

[4] Derucher K N.Analysis of concrete bridge piers for vessel impact [C]∥Proceedings of Sino-American Symposium on Bridge and Structural Engineering.China:1982.

[5] Pedersen P T,Valsgaard S,Olsen D and Spangenberg S.Ship impacts: bow collisions[J]. International Journal of Impact Engineering,1993(2):163 -187.

[6] Consolazio G R,Cowan D R.Nonlinear analysis of barge crush behavior and its relationship to impact resistant bridge design[J]. Computers and Structures,2003(81):547 -557.

[7] 刘建成,顾永宁.基于整船整桥模型的船桥碰撞数值仿真[J].工程力学,2003,20(5):155 -162.

[8] 高震,顾永宁,胡志强.结构冲击试验的校准计算[J].工程力学, 2003(S):456 -460.

[9] 美国LSTC公司.LS-DYNA 960 User's Manual,2001.

[10]叶贵如,茅兆祥.船桥正碰撞的非线性有限元仿真分析[C]∥2004年全国桥梁学术会议论文集.北京:人民交通出版社,2004.

[11]王自立,顾永宁.应变速率敏感性对船体结构碰撞性能的影响[J].上海交通大学学报,2000,34(12):1704 -1707.

[12]A Glykas,P K Das.Energy conservation during a tanker collision [J].Ocean Engineering,2001(28):361 -371.

[13]Saul R and Svensson H.Means of reducing consequences of ship collisions with bridge and offshore structures[C]∥IABSE Colloquium on Ship Collision with Bridge and Offshore Structures.Copenhagen: 1983.

Numerical Simulation Research of Nonlinear Finite Element on the Collision between Ship and Energy Dissipater for Bridge Structure Anti-collision

WU Jian-qiang,DING Qing,LIDe-hui,Deng Lei
(Jiangxi Research Institute of Communications,Nanchang 330038,China)

The collision between ship and bridge is a complicated nonlinear dynamic-response process. Nonlinear finite element technique can well solve the problem of ship-bridge collision.This paper briefly describes the basic principle of this technique.Based on the basic theory of collision simulation,the process of straight collision between the ship and the energy dissipater of bridge structure anti-collision is simulated.The whole time-course concerning the collision force,energy transformation and the plastic deformation of energy dissipater of anti-collision is detailed described and simulated meticulously allround.Compared with the results produced by the traditional quasi-static theory,the results by nonlinear finite element technique ismore accurate.The plastic deformation(collision depth)of energy dissipater of bridge structure anti-collision provided in this paper is of important value to the design.

ship-bridge collision;nonlinear finite element;energy dissipater for anti-collision; plastic deformation

U443.26

A

1004 -2954(2012)10 -0029 -05

2012 -02 -24

江西省交通厅科技项目(2011H0018)

伍建强(1979—),男,工程师,2005年毕业于西南交通大学桥梁与隧道工程专业,工学硕士。