四川省白马钒钛磁铁矿床铁品位分布地质统计学研究
黄 继,肖光莉,刘 伟,王 欢,向 虎
(四川省煤田地质工程勘察设计研究院,四川成都610045)
固体矿产勘查就是针对矿产资源中的固体物质进行的勘查,在区域地质调查和成矿预测的基础上,根据国内外矿产品市场的需求,运用成矿理论,采用有关的勘查技术手段和方法,对有关的矿产资源进行的专门性的地质调查研究工作.其主要任务就是通过一定数量的露头、钻孔、探槽及坑道提供的有用信息(如化验分析数据及岩矿标本)的研究,来揭示成矿地质条件,预测和普查矿床,对己经发现的矿床查明其规模、形态、产状及质量特征、工业应用条件,研究其成因,最后对它们做出总的工业评价.1951年,南非地质学家、采矿工程师克里格(D.G.Krige)根据南非金矿的具体情况提出了计算矿产资源量的方法:即按照样品与待估块段的相对空间位置和相关程度来计算块段品位及储量,并使估计误差为最小.1962年,马特隆(G.Matheron)经过对克里格提出的方法进行深入研究,提出了区域化变量(regionalized variable)的概念,产生了地质统计学[1].生产实践证明,地质统计学具有强大的生命力,它在地质科研、找矿勘探、采矿设计及矿山地质等领域日益显示出优越性,取得了一定的经济效益[2].
本次研究采用地质统计学原理和方法,通过对四川省米易县白马钒钛磁铁矿区及及坪矿段主矿体25个钻孔的2124个样品品位分布的分析和研究,探求其分布规律,为矿山的进一步开发和生产提供有意义的决策依据.
1 矿区地质概况
白马钒钛磁铁矿区大地构造位置处于康滇地轴中段,地跨康滇地轴深断裂系的安宁河深断裂带,幔源及壳源重熔物质极其丰富.区内各时代地层都有发育并出露,地层、构造、岩浆组合类型多样,具备不同类型铁矿生成的区域地质条件.
1.1 地层与构造
区内地层在矿区外围零星分布,有前震旦系会理群天宝山组、灯影组,二叠系峨眉山玄武岩以及第四系.
区内构造较复杂.主要褶皱为南北向的茨达-撒莲背斜.白马岩体产于该背斜的核部,岩体形态及空间分布位置与背斜核部相吻合.背斜轴线及白马岩体走向均近于南北向,与区域构造线方向一致.
区域性南北向断裂(昔格达断裂及安宁河断裂)分别在白马岩体东、西侧通过,北北东向张性剪切断裂(茨达断裂)通过岩体北部.上述断裂在白马地区交汇,形成一个剪切拉张地带,对白马矿体的形成起到控制作用.矿区成岩成矿后的构造十分发育,主要为南北向及北东向两组断裂,构成矿区内的构造格架(如图1所示).
1.2 岩浆岩
区内与钒钛磁铁矿有关的岩浆活动主要为华力西早期的基性—超基性岩浆侵入活动.空间上与此有一定关系的还有华力西晚期辉长伟晶岩、辉绿岩脉,二叠纪玄武岩,燕山期伟晶岩脉,印支期角闪正长岩、石英角闪正长岩等❶四川省地质矿产勘查开发局106地质队.四川省米易县白马钒钛磁铁矿区及及坪、田家村矿段勘探地质报告.1988..
1.3 矿体概况
白马钒钛磁铁矿区共圈定4个工业矿体,其中Ⅰ、Ⅱ号矿体是主矿体,本文研究重点即为Ⅰ、Ⅱ号矿体.该含矿层之矿体为一个厚大层状矿体.其形态产状与含矿层一致,呈稳定的层状产出,走向近南北,倾向西,倾角 50~70°.
矿石结构以海绵陨铁结构为主,是该含矿层矿体中稀到中稠浸染矿石的主要结构类型.其次是粒状嵌晶结构和假斑状嵌晶结构,这两种结构主要分布在矿体底部的矿石中.矿石构造以中等至稠密浸染状构造为主,次为稀疏浸染状构造,在位于含矿层顶、底部矿体的矿石还见有中等至密集条带状构造.

矿体沿走向南北长大于5000 m,并沿倾向方向向深部继续延伸.
2 矿石品位的统计和分析
白马钒钛磁铁矿区位于四川省米易县白马镇,为一构造侵蚀中山区,南北长约9 km,东西宽约5 km,面积约45 km2.及及坪矿段是其主要矿段之一.因为研究及及坪矿段铁品位分布特征,所以将铁的品位值作为区域化变量对待,对它的研究应限制在一个品位值具有相关性的空间里,即应使用落在矿体内的样品进行统计分析.本文采取了以边界品位15%为起点进行统计分析.
2.1 铁品位统计分布特征
参与计算的品位数据来源于各个勘查线的钻孔资料,选取25个钻孔共计2124个样品,利用SPSS11.5软件绘制出铁品位分布直方图(图2).从直方图中可以看出,样品符合正态分布,因此我们就可以计算出其变异函数.
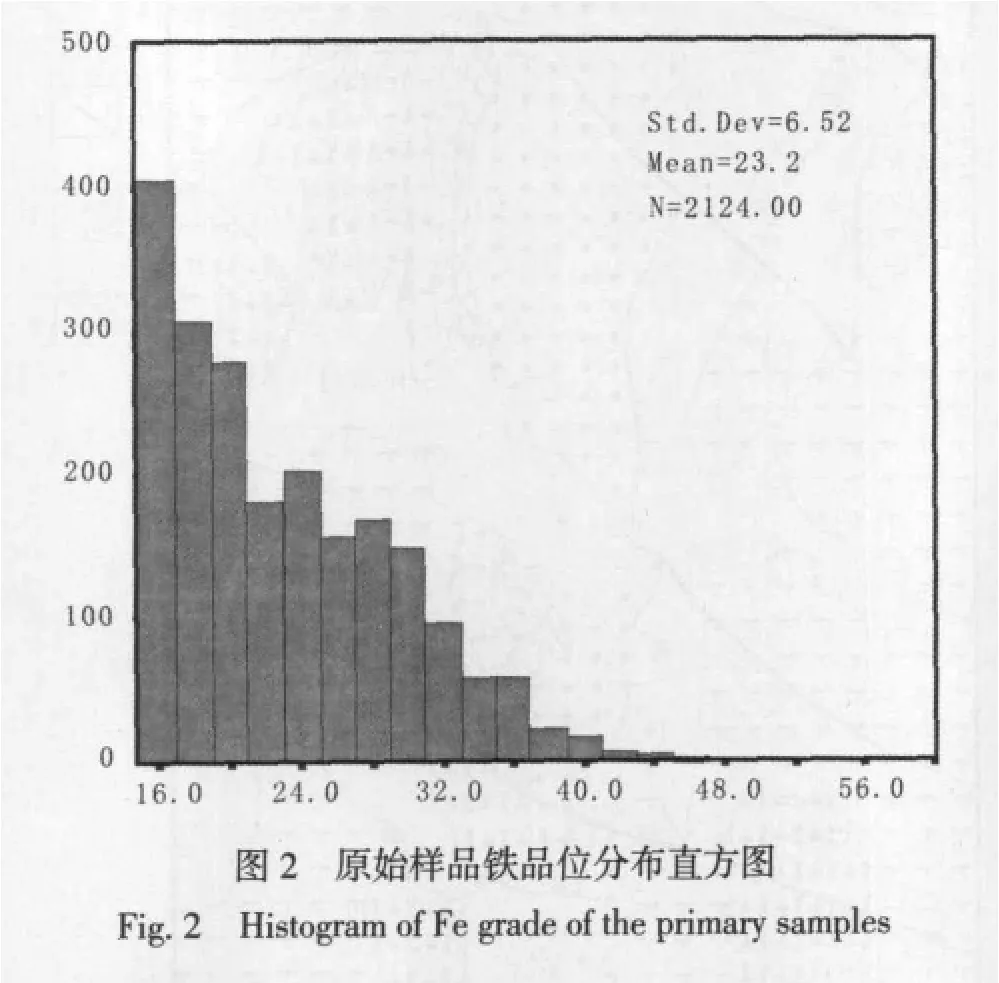
铁品位统计数字特征如下:

从表1中可以看出,铁最高品位值为59.6%,为特高异常值.特异值即特高品位,是由于个别样品取在矿化局部富集的地段产生的,特高品位的存在往往会影响矿体总的品位分布和估值,通常情况下必须对其进行处理[1].
白马矿区及及坪矿段矿床品位变化简单,因此选用3倍标准差的方法进行特高品位处理.但若某一地区连续出现特高品位时,则认为是富矿地区,不进行处理[3].由于对原始样品统计分析得出的样品均值为23.21,标准差为6.52,因此特高品位下限值定为23.21+3×6.52=42.77,若出现大于特高品位下限值时均用42.77作代值处理.特高品位处理后的品位分布规律、直方图如图3.

表1 原始样品数据统计表Table 1 Statistics of primary samples

从原始样品铁品位分布直方图(图2)可看出Fe元素品位数据呈现出较为明显的偏畸.在进行特高品位处理之后,从表2和图3中均可以看出各项结果均有所下降,2110个样品中的大部分品位数据集中在(16,29)区间内出现.

表2 特高品位处理后样品数据统计表Table 2 Statistics after outlier processing
2.2 实验变异数据的计算
实验变异数据按下式进行计算:
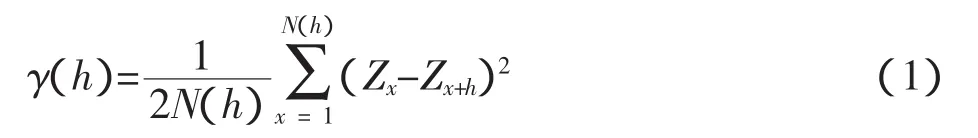
式(1)中:N(h)是滞后距为h时参加实验变异函数计算的样品个数,h为滞后距,Z为区域化变量在空间点上的品位值.
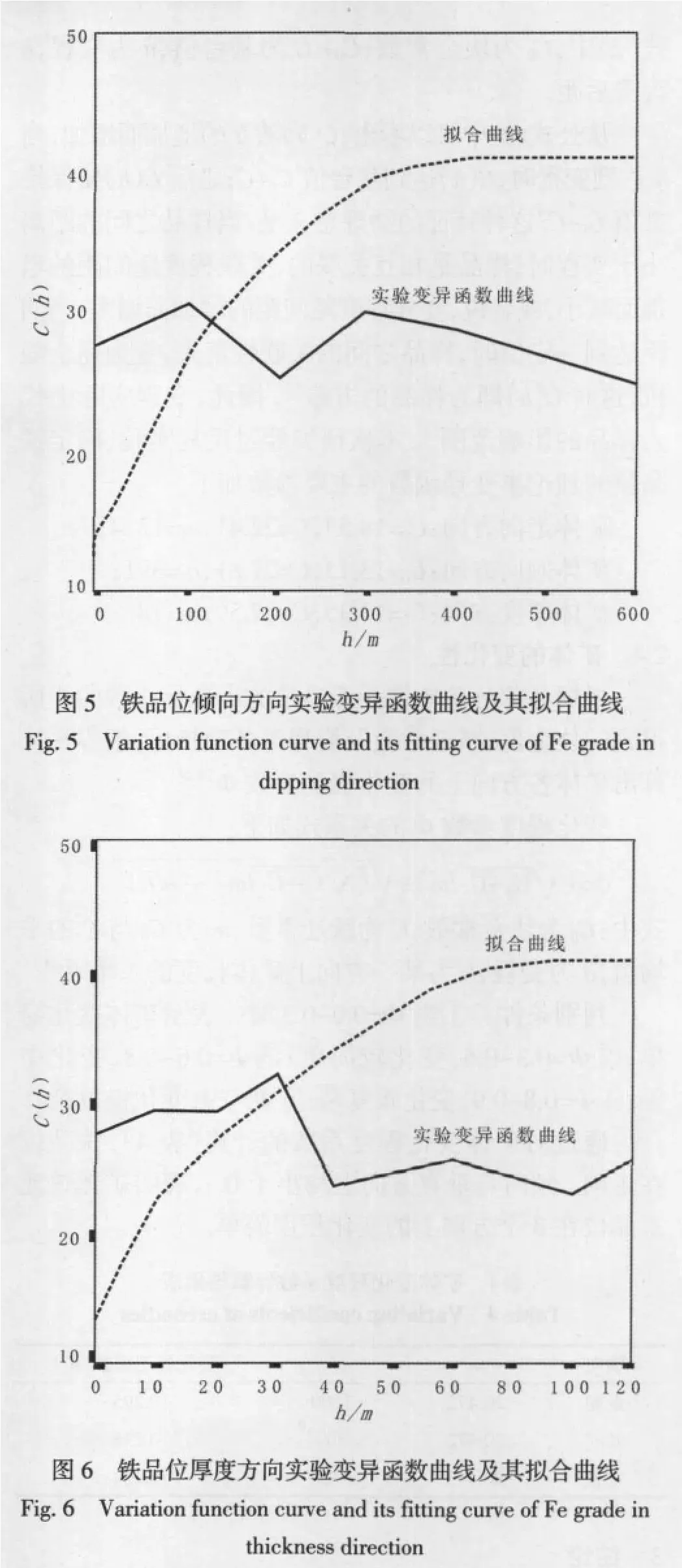
在进行金属元素品位变异函数分析时,分别沿矿体走向、倾向与厚度3个方向进行变异函数分析[4].根据矿床产出特征,确定各分析方向计算时实验变异函数角度及距离参数(见表3).同时绘制出3个方向的实验变异函数曲线图,图4、5、6实线所示为铁品位的实验变异函数曲线.

表3 各分析方向计算时变异函数角度及距离参数Table 3 Parameters for variation function analysis

2.3 理论变异函数的曲线拟合
从该矿的实验变异函数曲线的特征来看(如图4、5、6),从几组样品得到的实验变异函数,虽然数据点的分布不很规则,但仍可看出C(h)随h首先增加,然后趋于稳定,符合球状模型的特点,因而采用实验变异函数球状模型用加权多项式回归法分别对走向、倾向、厚度3个方向进行拟合.球状模型的公式为[5-6]:
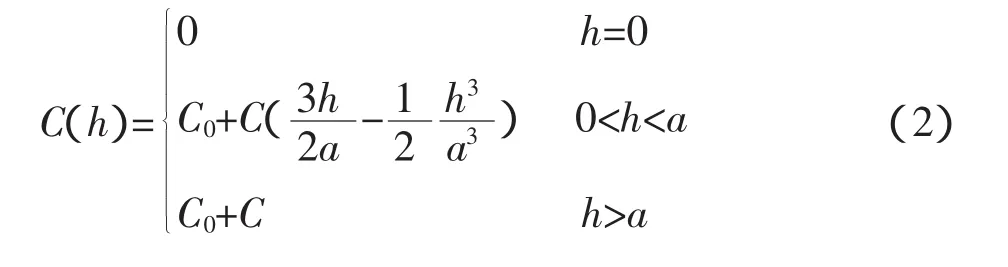
式(2)中:C0为块金常数,C0+C 为基台值,a为变程,h为滞后距.
从公式(2)中可以看出,C(h)随 h的增加而增加,当h 达到变程时,C(h)达到基台值 C0+C;之后 C(h)便保持常值C0+C.这种特征的物理意义是:当样品之间的距离小于变程时,样品是相互关联的,关联程度随间距的增加而减小,或者说,变异程度随间距的增加而增大;当间距达到一定值时,样品之间的关联性消失,变为完全随机,这时 C(h)即为样品的方差[7].因此,变程实际上代表样品的影响范围[8].本次研究经过反复实验,确定铁品位的理论半变异函数的主要参数如下.
矿体走向方向:C0=18.53,C=22.41,a1=1214;
矿体倾向方向:C0=13.13,C=27.81,a2=391;
矿体厚度方向:C0=13.35,C=27.59,a3=78.
2.4 矿体的变化性
根据各部分矿体铁元素品位的半变异函数曲线所得到的块金值、跃迁常数及变程等各项指标,很容易计算出矿体各方向上的变化程度参数Ф[9-10].
变化程度参数Ф的关系式如下:

式中:C0为块金常数,C为跃迁常数,m为C0与C的平均值,a为变程,L为某一方向上矿体长度的一半[11-12].
判别条件:①当Φ=0.0~0.3时,表示矿体变化简单;②Φ=0.3~0.6,变化较简单;③Φ=0.6~0.8,变化中等;④Φ=0.8~0.9,变化较复杂;⑤Φ>0.9,变化极复杂.
通过对矿体变化程度系数的计算(表4),铁品位在走向、倾向与垂直方向上均小于0.3,表明矿体铁元素品位在3个方向上的变化程度简单.

表4 矿体变化程度系数计算结果表Table 4 Variation coefficients of orebodies
3 结论
1)白马钒钛磁铁矿矿床铁元素的品位分布均具有一定的规律性,铁元素在倾向上较走向与垂向上变化有规律性.这与该矿区勘查成果基本吻合,矿体在走向上受4组近东西向断层影响,导致走向上主矿体空间赋存状态差异较大.
2)白马铁矿床铁品位统计分布呈单峰的正态曲线,并且矿体变化程度系数值较小,说明该矿区成矿作用单一,矿化较均匀.
3)铁品位在3个方向上的变异函数在一定距离范围内呈上升趋势,随后逐渐平缓,最后达到水平,说明当样品之间的距离小于变程时,样品是相互关联的,关联程度随间距的增加而减小.当矿体走向、倾向、垂直这3个方向的距离分别达到1214、391、78 m时,铁品位之间的相关性消失,变为完全随机.
4)工程间距只有小于变程时才能控制矿体的变化,根据矿区复杂的构造情况,目前矿区采用400 m×400 m的工程间距探求333资源量,拟采用200 m×100 m工程间距控制332资源量,应该说是合理的.
5)建立了矿体走向、倾向、垂直3个方向的矿化数学模型,对铁品位分布特征进行统计.结果表明,模型确定合理,所统计的数据真实可靠,真实形象地体现了主矿体铁品位的空间分布规律.为下一步用普通克立格法计算矿体品位和储量计算打下了基础,为以后在攀西地区找类似华力西期基性、超基性铁矿床起到了一定的指导作用,为矿山生产设计以及建立整个矿体的三维模型提供了理论依据.
[1]夏正清.基于灰色系统理论和地质统计学的Cu品位估算研究[D].湖南:中南大学,2009.
[2]马田生,寇轶勇,阳正熙,等.地质统计学在山东焦家金矿床深部含矿性预测中的应用[J].地质找矿论丛,2005,20(3):176—181.
[3]罗周全,刘晓明,吴亚斌,等.地质统计学在多金属矿床储量计算中的应用研究[J].地质与勘探,2007,43(3):83—87.
[4]万昌林,朱利平,高祥.应用地质统计学评估福建某铜矿资源[J].金属矿山,2002(6):140—143.
[5]李莲花,李卉.辽宁弓长岭一矿区铁矿石品位分布的地质统计学研究[J].辽宁地质,1998(2):126—130.
[6]李岭.地质统计学及其在某铜矿山储量计算中的应用[J].矿业研究与开发,2004,24(5):21—23.
[7]冯超东,杨鹏,胡乃联.克立格法在SURPAC软件中的实现及应用[J].金属矿山,2007,370(4):55—77.
[8]郑文宝,黎枫佶,唐菊兴,等.西藏墨竹工卡地区甲玛矽卡岩型铜多金属矿体的变化性[J].地质通报,2010,29(10):1487—1494.
[9]余海军,李文昌,尹光候,等.普朗铜矿床铜品位分布地质统计学研究[J].地质与勘探,2009,45(4):437—443.
[10]侯景儒,黄竞先.地质统计学在固体矿产资源/储量分类中的应用[J].地质与勘探,2001,37(6):61—66.
[11]贾明涛,潘长良,王李管.克服地质统计学矿床建模中主观因素影响技术研究[J].地质与勘探,2003,39(4):73—77.
[12]侯景儒,黄竞先.地质统计学及其在矿产储量计算中的应用[M].北京:地质出版社,1982:35—46.

