改进SVC算法在雷达信号分选中的应用

赵贵喜，穆成新，刘永波，王睿东

（解放军93163部队，哈尔滨 150001）

0 引 言

随着现代科学技术的不断发展，各种体制雷达不断涌现，使得雷达信号环境日益复杂，这就对雷达信号分选提出了新的要求。传统的基于利用脉冲重复间隔（PRI）单参数进行信号分选的方法已经越来越不能适应当前复杂的电磁环境。支持向量聚类（SVC）是由Asa Ben.Hur等人在支持向量机的基础上提出的一种非参数聚类算法，被广泛应用于各个领域。

本文将SVC聚类算法应用到雷达信号分选中，在利用SVC进行聚类分析时发现，SVC不仅时间复杂度高，而且在处理分布复杂、不均匀的样本时，识别率较低。K－Means聚类算法在处理大量数据时时间复杂度不高，但是存在需要事先确定数据聚类数目的明显缺陷，本文将SVC聚类算法与K－Means聚类算法相结合，提出了联合聚类分选算法，并通过仿真实验验证了算法的可行性。

1 SVC算法

SVC聚类是2001年由Asa Ben－Hur等人在支持向量机的基础上提出一种非参数聚类算法。它的基本思想是：将样本点经过一个非线性映射映射到一个高维特征空间，并在此空间中寻找一个包围所有样本点且具有最小半径的超球，当这个球面被映射到数据空间时，能分割成几个部分，每个部分都包含了独立的数据点聚类，位于球表面的点即为支持向量，一个高维空间的球在原来的空间中可以是任意的形状。

SVC通过二次规划问题求解，得到全域最优解，而且能处理任意形状的聚类，并划分有重叠区域的聚类形状，对噪声也能有效分析［1－3］。

定义1：设数据空间x i∈Rd，数据集｛x i｝∈X，包含d维空间i个数据点，运用非线性变换将数据从x映射到高维特征空间，寻找Hilbert空间最小包络x点的超球体半径R。为了发现带有软边界的最小包络球体，表达为：

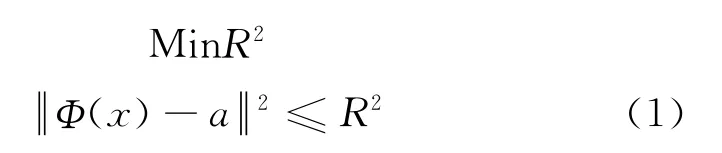
式中：||·||为欧基里德函数；a为球体中心。

引入松弛系数ξj，式（1）变为：

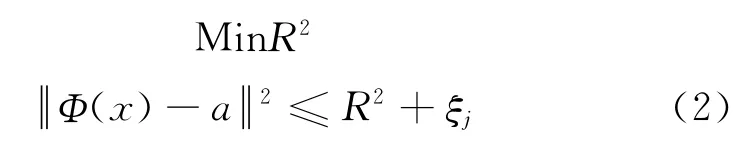
引入拉格朗日乘式：

如果βi＝C，则表示点x i映象位于特征空间的球体之外，被称作约束支持向量（SV）。如果0＜βj＜C，则点x i的映像将位于特征空间球体的表面。这样的点被当作是支持向量（SV）。SV位于聚类边界，基本支持向量（BSV）位于边界之外，其他所有点都在边界之内。

用高斯核函数K（x i，x j）表示点积，则得到只包含βj的Wolfe对形式为：

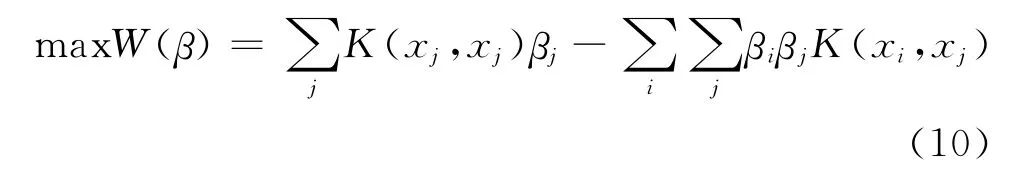
SVC算法在处理中等规模的数据样本时，计算和存储非常困难，而且对于分布复杂、不均匀的样本，寻找获得全局最优聚类配置的参数值极其困难，容易陷入局部最优解，而非全局最优［4－5］。

2 KSVC联合聚类算法

2.1 K－Means聚类算法

K－Means聚类算法由 Mac Queen首先提出，属于聚类方法中一种基于划分的方法，它是一种较简单的迭代优化方法。该算法首先随机地选择k个对象，每个对象初始地代表了一个类的平均值或中心。对剩余的每个对象，根据其与各个类的中心距离，将它赋给最近的类，然后重新计算每个类的平均值。这个过程不断重复，直到准则函数收敛。通常采用平方误差准则。

K－Means聚类算法选用雷达数据的脉冲到达角（DOA）tDOA、载频（RF）fRF和脉宽（PW）τPW三维参数作为聚类分选参数。设某一信号p i经过标准化处理后，取出tDOA、fRF和τPW这三维数据，成为新的形式p′i（tDOA，fRF，τPW），i＝1，2，…，N，这样就形成了雷达脉冲描述向量集合P′＝ ｛p′1，p′2，…，p′N｝。K－Means聚类就是要找到P′的一个划分V k＝｛C1，C2，…，C k｝，使目标函数f（V k）值收敛最小。f（V k）为：

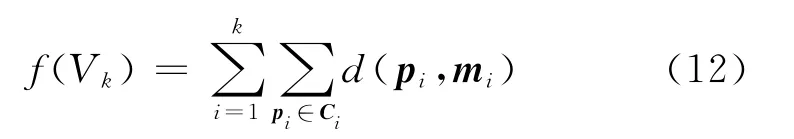
从K－Means聚类算法分选流程上可以看出，有2个关键步骤可以影响聚类结果：

高等动物细胞核直径一般为5～10 μm，高等植物细胞核直径一般为5～20 μm。教师利用超轻黏土、废弃胶头滴管胶帽和细铁丝等材料，分别模拟核模、核孔复合体和核酸，制作放大约4万倍的细胞核模型（即直径约20 cm），如图1所示。

（1）聚类数目k在算法开始运行之前必须确定，然而这个k值的选定往往是困难的。很多时候，并不知道给定的全脉冲数据应该分成多少部雷达才最合适。如果聚类数目k设置不正确，聚类分选会出现严重的“增批”和“漏批”现象。在实际运用中，k值要么直接给定，要么根据经验来选取，没有一个比较通用的好方法。这是该算法的局限性。

（2）初始聚类中心的选择。这是K－Means算法的关键步骤，这种随机选择初始聚类中心的方式常常使算法在不同的运行中产生不同的聚类结果，很多时候有可能得不到最佳的聚类结果，算法常以局部最优结束，甚至出现无解。

2.2 联合分选算法

K－Means聚类算法当选定合适的初始聚类中心和合适的聚类数目时会取得良好的分选效果，而SVC聚类分选算法是一种无监督聚类分选算法，不需要事先知道数据的类别数目。

基于以上考虑，本文将2种聚类算法相结合，利用SVC算法事先确定雷达信号数据的分类数目，再利用K－Means分选算法进行分选，从而缩短聚类分选时间和复杂程度。

算法描述如图1所示。

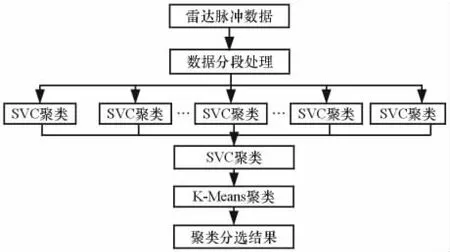
图1 算法描述图

联合聚类算法采用雷达脉冲到达角tDOA、脉冲重频fRF和脉冲宽度τPW3个参数联合分选，按如下步骤执行：

（1）读入雷达脉冲数据，提取雷达信号参数tDOA、fRF和τPW进行数据标准化处理；

（3）对每段数据分别进行SVC聚类处理；

（4）将分段聚类的数据再进行SVC聚类处理，得到数据的初始划分；

（5）运用聚类算法提供的初始聚类数目和初始聚类中心作为输入，用K－Means算法进行聚类分析；

（6）统计聚类信息，输出结果。

3 仿真实验

实验模拟了4部雷达，按照到达时间进行混合，对同时到达的信号进行丢失处理，共320个脉冲信号。雷达参数设置如表1所示。

4部雷达混合数据经过标准化后，分布如图2所示（图中“＊”代表雷达脉冲）。

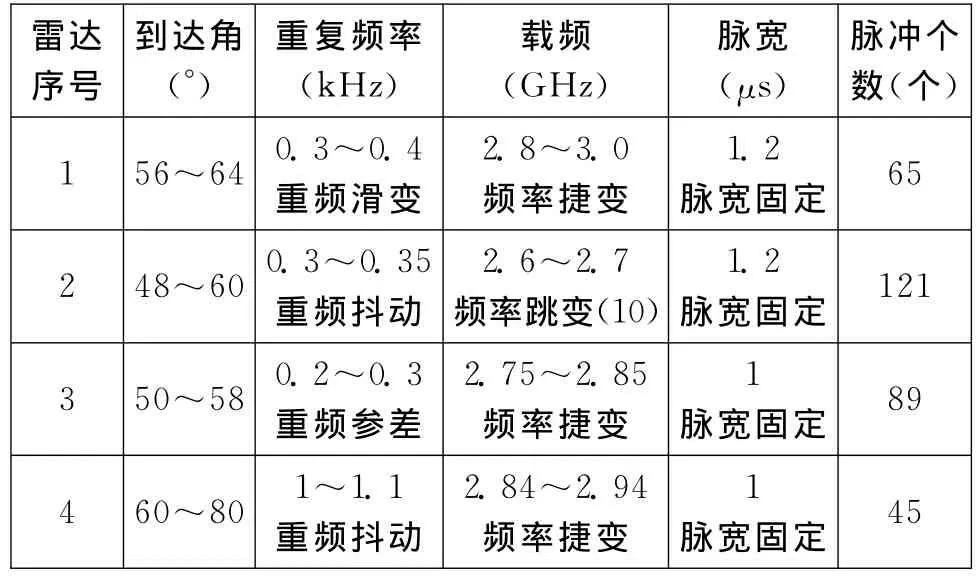
表1 雷达仿真数据

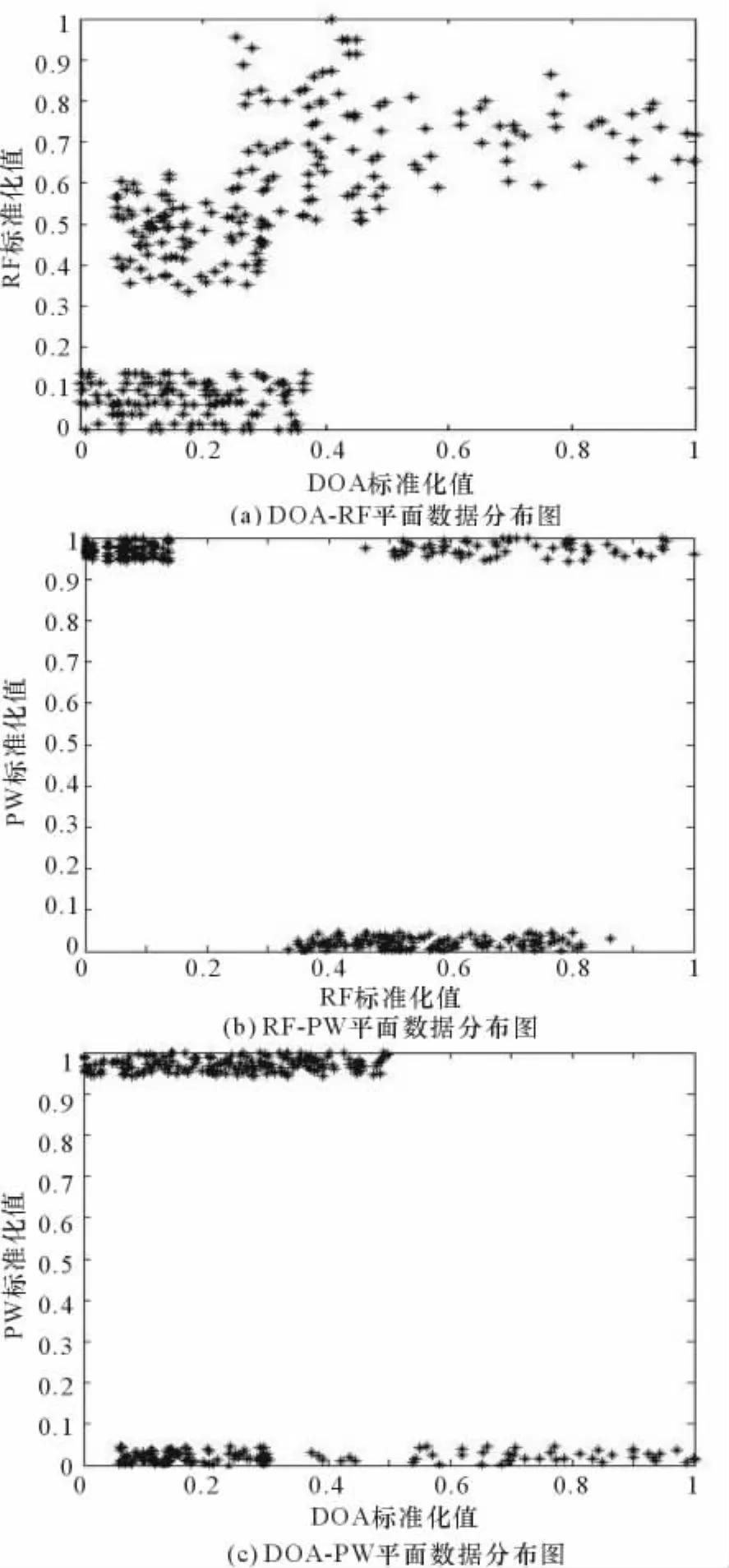
图2 雷达混和数据二维属性分布图

从图2（a）、2（b）、2（c）的雷达混合数据分布图可以看出，4部雷达在不同的属性维度上混合严重，从图3（d）的分选结果可以看出本文提出的联合聚类分选算法准确地将混合数据分选成了4类，并且每部雷达数的分选数目正确。

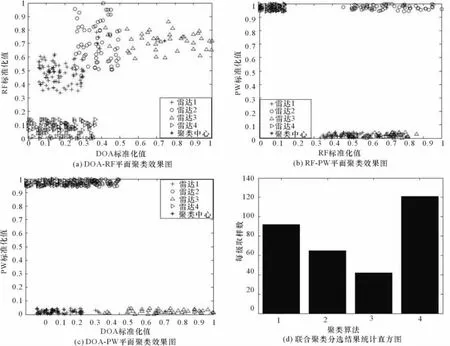
图3 联合聚类分选效果图

通过详细的对比可以看出雷达A中有5个数据被错误地分选成了雷达B，雷达B中的5个数据被错误地分选成了雷达A，雷达C和雷达D均正确分选，分选正确率达到96.88%。

4 结束语

本文提出的基于SVC聚类和K－Means聚类的联合聚类分选算法可以很好地分选出雷达信号，经过仿真实验验证取得了比较理想的效果。这只是本文对雷达信号分选算法的一种尝试，还存在很多缺点，如处理大量数据时，消耗时间较长，参数设置困难，这些都有待进一步研究。

［1］苏意玲.一种基于支持向量机和聚类的Web挖掘新方法［J］.计算与现代化，2009，172（12）：33－35.

［2］蒋加伏，赵嘉，胡益红.一种基于支持向量聚类的图像分割 方 法 ［J］.计 算 机 工程 与 应 用，2009，45（30）：165－167.

［3］孙德山，李海清.基于线性规划的支持向量聚类算法［J］.计算机工程与设计，2010，31（6）：1305－1307.

［4］Francesco Camastra，Alessandro Verro.A novel kernel method for clustering［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，2005，27（5）：801－805.

［5］孙德山，吴今培.基于线性规划的多类支持向量机算法［J］.计算机科学，2005，32（10）：160－163.