基于Matlab带阻滤波器电路设计及参数寻优

陈晓冲，屈 蕾

(中航工业西安飞行自动控制研究所，陕西西安 710065)

Matlab［1］作为一种常用的大型工程软件，包括数值计算、程序设计、信号处理等多种功能，目前已成为辅助电路分析最为通用的软件之一。实际工作中，当对电路进行分析设计时，会涉及到大量的计算，而这些计算十分繁冗。为此，可借助于Matlab本身自带的函数进行编程解决电路计算问题，同时将电路分析中频繁遇到的计算问题编写成函数，以提高电路分析的效率，取得了良好的效果。

1 带阻滤波器

信号处理中，一般只允许一定频率范围的信号通过，而实际信号频率的范围可能较大，这就需要使用带阻滤波器进行信号处理。

带阻滤波器是指能通过大多数频率分量，但将一定范围的频率分量衰减到极低水平的滤波器，用来抑制一定频段内的信号［2］。带阻滤波器可分为窄带滤波器和宽带阻滤波器。窄带阻滤波器一般用带通滤波器和减法器电路组合起来实现，窄带组滤波器通常用作单一频率的陷波，又称为陷波器。宽带阻滤波器通常用低通滤波器和高通滤波器求和实现。理想带阻滤波器在阻带内的增益为零［3］。带阻滤波器的中心频率f0和抑制带宽BW之间的关系为

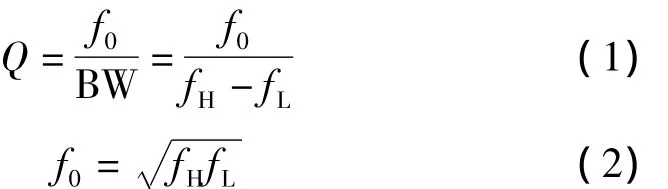
式中，Q为品质因数。fH为带阻滤波器的上限频率。fL为带阻滤波器的下限频率，其中fH＞fL。带宽BW越窄，品质因数Q越高。

2 目标函数分析

文中要实现的带阻滤波器函数如下

对该函数进行分析，可以先分析典型的二阶带通滤波器，其形式如式(4)所示。通过适当的电路形式实现以上函数，且电路中各参数值在要求在标称值范围内

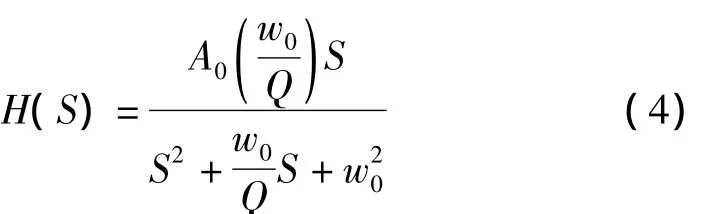
将二者进行对比，可发现:当用1减去H(S)时，可得到所需的结构形式。其典型的电路形式如图1所示。

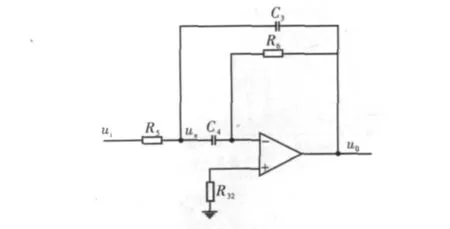
图1 带通电路图

根据虚短虚段原理，可得到该电路图的节点电压方程组

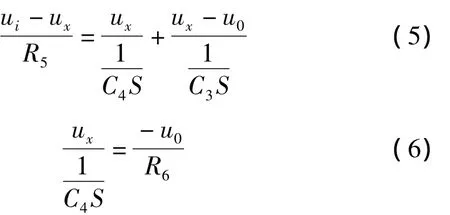
整理式(5)和式(6)可得

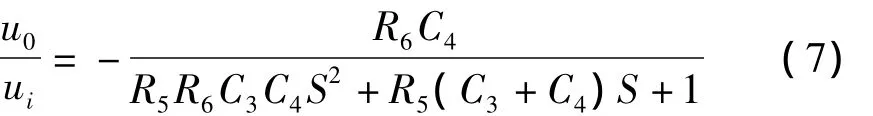
将式(5)与式(2)对比可得

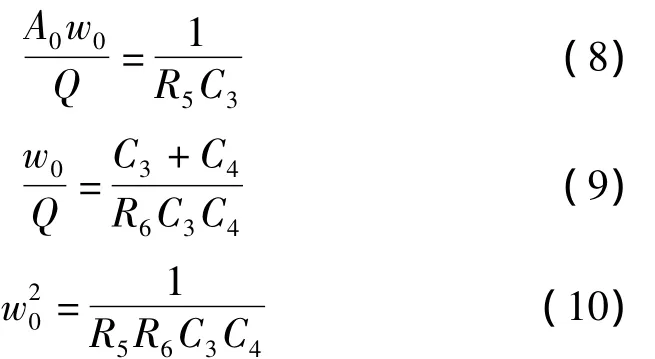
由式(10)可得到中心频率的另一计算公式

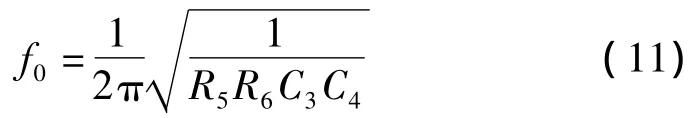
3 带阻滤波器的电路实现

通过以上分析，带阻滤波器在电路的实现形式上，采用带通响应综合成带阻响应，即带通滤波器和减法器组成，得到带阻滤波器电路，其电路形式如图2所示。

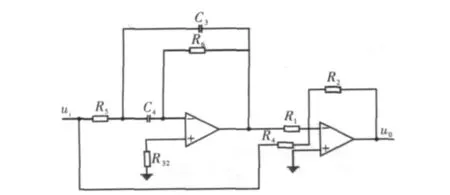
图2 带阻电路图

将R1之前的带通滤波器输入看作一个整体，记为ud，则根据加法器电路原理有

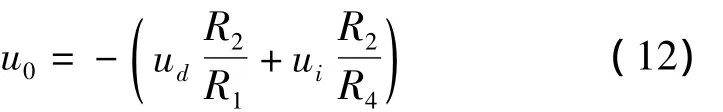
此处，ud的代数式为式(7)，为满足式(3)，必须满足R2=R4，代入整理，并与式(3)对照可得

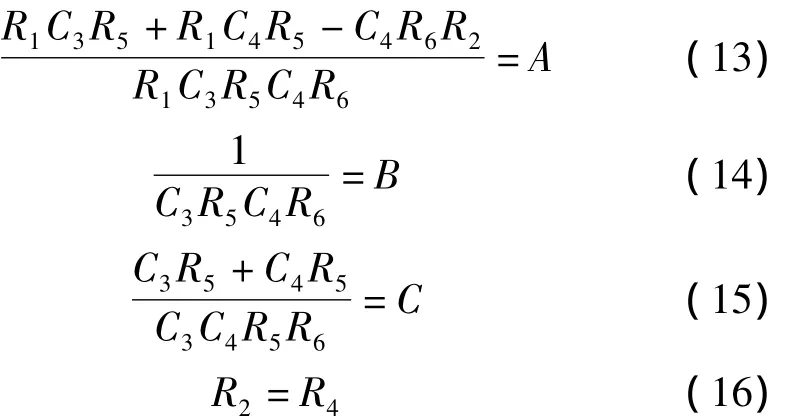
4 Matlab参数计算及寻优

由上述分析可见，式(13)～式(16)包含7个未知变量，任意确定其中4个参数，该方程组为包含3个未知变量的非线性方程组，手工计算难度较大，且又要使得解析值为电阻或电容的标称值，更使计算量较大，重复性强。但运用 Matlab的优化工具箱函数Solve，就能对其方便地求解，Slove函数用来对一般的代数方程，包括非线性和超越方程进行求解，且可以解出关于指定变量的解析方程，该函数相当于对矢量方程等式左边就目标值0，进行寻优求值。for循环语句可以完成重复寻优的工作。寻优的思想是将电阻和电容的标称值作为列表，输入Matlab程序中，每一参数进行寻优，使得每个参数均为标称值。程序流程如图 3 所示［4－5］。

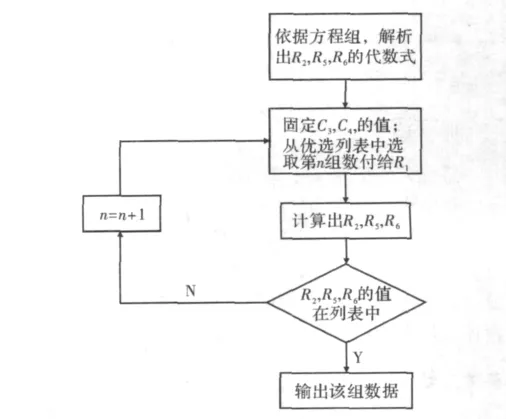
图3 程序流程图

在Matlab环境下，编写m文件，实现参数计算以及寻优。

以上计算机寻优计算，使电容值取定值，电阻值进行寻优，可得到多组解值，表1是在A、B、C都给定的条件下寻到的满足要求的结果，若还要缩小结果的可选范围，可再加入误差范围要求、品质因子等约束条件，使得可选范围缩小，同时还可加入如频谱分析等其他功能。

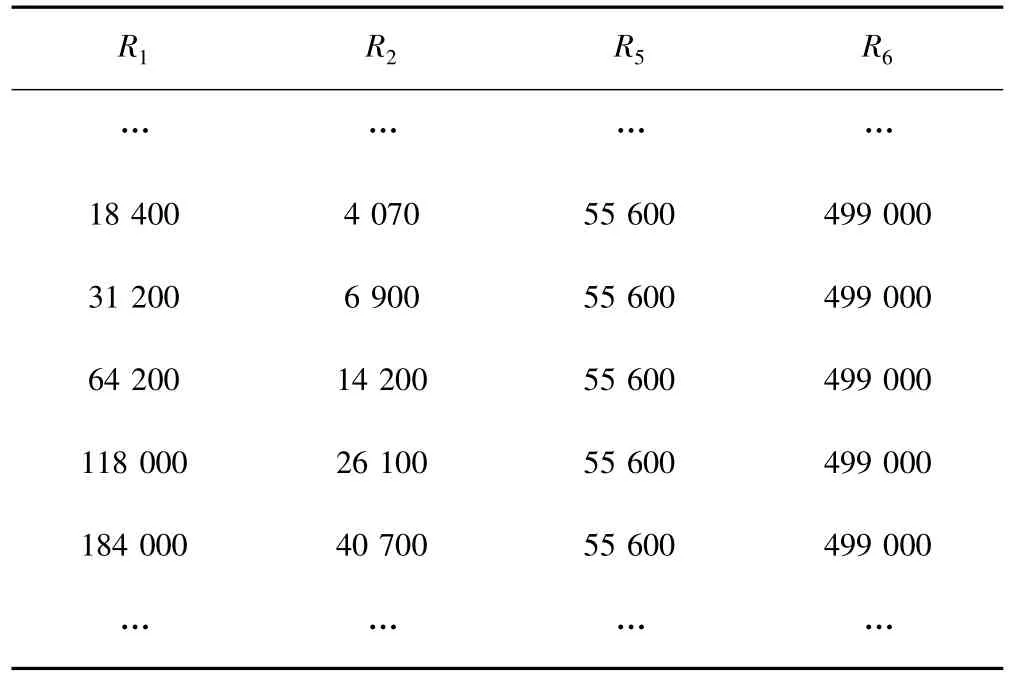
表1 电阻阻值寻优结果

5 结果分析

对所需要设计的带阻滤波器的传递函数进行了Matlab仿真分析，对传递函数进行分析设计出相应的电路，并通过Matlab对该电路参数进行计算寻优后，应用PSpise电路仿真软件对该电路进行了仿真分析，并记录了实际电路测试的结果。现将3种结果绘制到同一张图上，其结果如图4所示，陷波频率Matlab仿真结果为9.55 Hz，电路Pspise仿真结果为9.568 Hz，实际电路中，由于电容带来的误差，使得实测值会有偏差，实测结果为9.48 Hz，误差度为0.7%，满足使用要求。

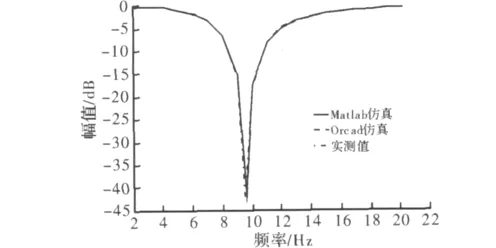
图4 带阻滤波器结果分析图

6 结束语

带阻滤波器在实际信号处理中应用广泛，而其参数的选取是个计算繁冗、重复性强的过程。文中根据已知带阻滤波器传函，设计相应的实现电路，该电路参数计算较为复杂，加之参数需符合标称值，更导致计算量大、繁琐，重复性强，但运用Matlab的计算功能，可以使问题简单化，且既使带阻滤波器的传函参数发生改变，也只需调整程序中相应的参数即可，使得电路设计过程大幅简化。

［1］ 张德丰.Matlab语言高级编程［M］.北京:机械工业出版社，2010.

［2］ 夏超英.自动控制原理［M］.北京:科学出版社，2010.

［3］ 曹良足，殷丽霞.小型带阻滤波器的结构与设计［J］.压电与声光，2010(6):125－128.

［4］ 姜春玲，史玲.基于Matlab的模拟滤波器设计［J］.山东交通学院学报，2004，23(8):89 －92.

［5］ 杨晔.基于带阻滤波器的无阻尼系统校正设计［J］.中国惯性技术学报，2010，19(2):65－68.