用支持向量机建模学习过程

刘宏义

(中国人民解放军边防学院信息化研究试验室，陕西西安 710108)

在当前的游戏开发中，最具有挑战性的工作是人工智能的编程。其中关键的部分就是学习过程。当游戏玩家不断地变化玩游戏的策略，学习系统就会遇到很多困难。经典的学习系统需要花费很多时间忘记旧规则，同时学习新规则。作为一种解决方法，文中为学习分类器引进了一个时间概念，这样，系统就可以很容易地忘记过去的事情。这里提出支持向量机(SVMs，Support Vector Machines)，这种技术可以应用于其他类型的分类器。

1 支持向量机

支持向量机(SVMs)是学习分类器。例如，神经网络学习分类器。但它们使用的概念略有不同。支持向量机(SVMs)是一个线性分类器的概括，与神经网络相比，SVMs关键的优越性是其创建和训练算法［2］。

1.1 线性分类器

在超平面的帮助下，线性分类器可以把输入空间分成两个部分:类A为类B。位于超平面上部的每一点属于类A，面位于超平面下部的每一点属于类B。图1显示了一个已分类的数据集。在式(1)定义的平面D是分类器的唯一参数。如果xi被分为类A和类B，如果分类器是经过训练的，这些数据的分类可以由式(2)和式(3)来实现。

〈x，y〉代表标准点积〈x，y〉=x1·y1+x2·y2+…

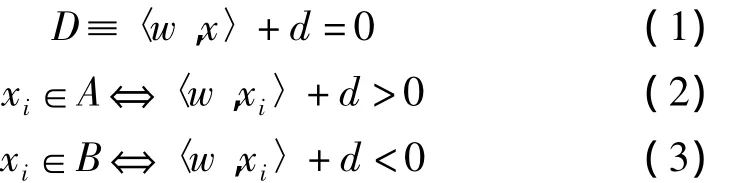
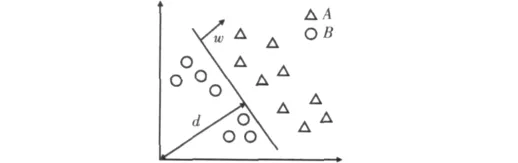
图1 线形可分离数据集

然而，由两个约束条件组成系统的训练并非无足轻重。如果具备式(4)和式(5)，那么分类的条件就变成了式(6)

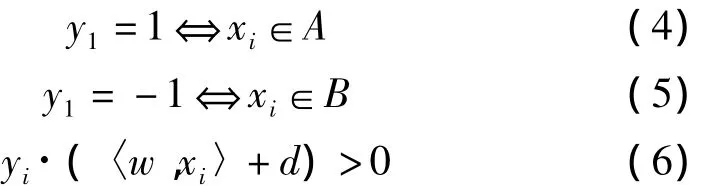
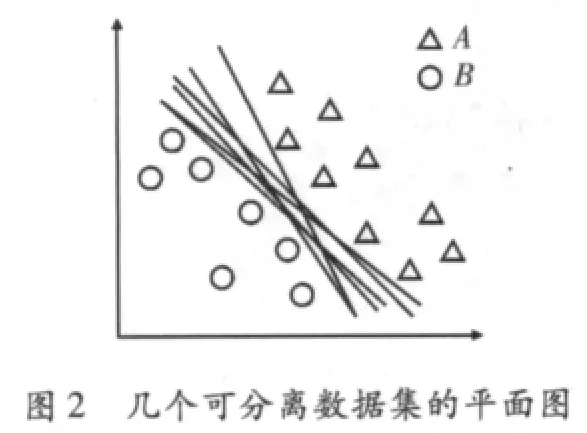
正如式(6)验证的每个点，训练就是要寻找w和d。但这里存在着无数个分离平面，需要从这些平面中选择一个。尽量选择一个最能概括分类器的平面。也就是说，使用一些没有包含在训练集合中的数据，也能得到比较好的结果。这决定使用式(7)，如同在图3中显示的那样，有两个分离平面，每一个平面对应一个yi值，平面间的距离称为边界。可以表明，边界是与成比例的［4］。

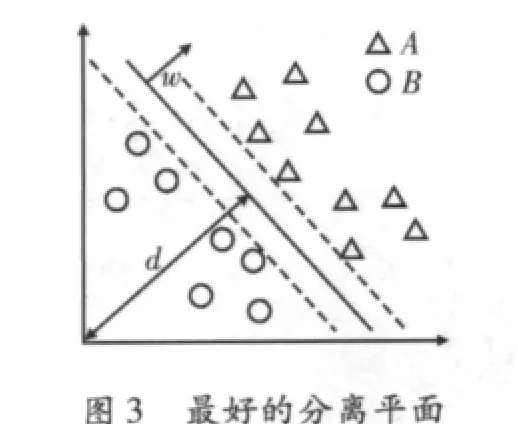
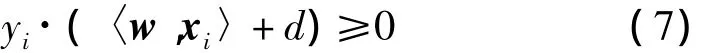
验证式(8)的那些点称为支持向量。这些点支持此解决方法，其分布在限定平面上，并且位于它们类的边缘

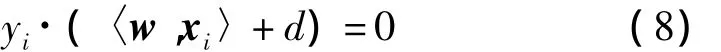
可以证明，向量w是支持向量的一个线性组合［1］。式(8)和式(9)的组合可被改写为式(10)，现在分类的条件与训练数据无关

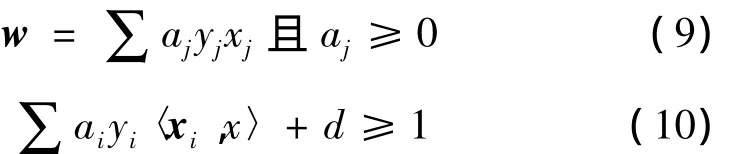
现在的训练在于寻找 ai和 d。每个不能验证式(8)的点，系数ai将为空。因此可以把它从解决方法中移走，这是训练所要达到的目标。支持向量及其相应的系数作为分类器的参数。

毕业论文要想设置不同的页眉和页脚，插入分节符是成功的关键。将光标定位到需要插入分节符的文字前。一般来讲，毕业论文的封面、摘要、目录和各章节都需要插入分节符，以便在这些内容处设置不同的页眉和页脚的内容。

图4表明的解决平面都依赖于支持向量，因为它们都共享法线w，这些平面必定互相平行。可以证明，去掉一个非支持向量的向量，解决方法并不改变。这是合乎逻辑的，因为它们的ai为空，所以不会改变分类器的参数。

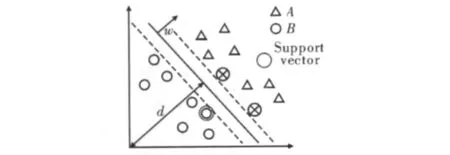
图4 在支持向量中的平面

如果想用一个新数据集来训练系统，没有必要添加整个旧数据集，需要的仅是旧数据集中的支持向量。

1.2 非线性可分离数据集的扩展

如果输入空间被转换成一个高维空间，非线性可分离数据集也可以变成线性可分离的。图5就显示了这样一个空间转化的概念。

图6(a)显示了一个具体的例子。如果试图用线性分类器为这些数据集分类，则无法获得分离平面。如果在式(11)的帮助下，把一维的空间转换成一个二维的空间，那么这时候数据集就是线性可分离的。图6(b)表示转换过程和一个成功的分离平面。这个举例虽然简单，但也表明这种转化为更高维空间的可行性。

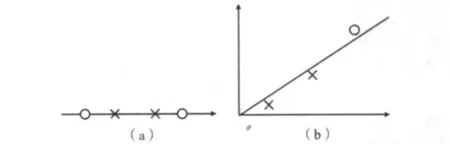
图6 通过使用转换成一个更高维空间来解决问题

1.3 核心函数

如果转换应用于每一个向量xi和w，式(10)就变成了式(12)。〈∅(xi)，∅(x)〉是两个转换向量的点积。尽管转换空间已成为高维的，但返回值将总是一个标量值。可以把〈∅(i)，∅(x)〉当成一个简单的函数，其功能就是要返回一个标量。这个函数称为kernel(K)。式(13)给出了这个函数K(x，y)定义。现在不需要强求知道∅(x)的值。此时的∅(x)也可以转换数据到一个无限纬度空间。作为一个举例，式(11)表示的等价核心的转换将在式(14)中计算。现在可以重写分类条件，最后形式如式(15)所示

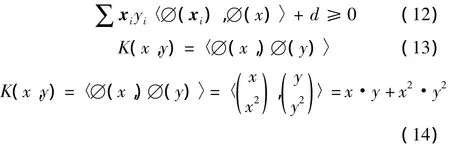
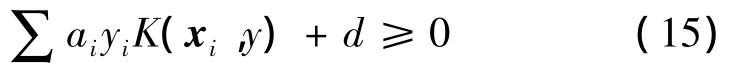
核心函数必须验证在文献［1］中可以看到的条件。这种情况下，一些∅(x)与核心函数匹配。式(16)中的核心函数具有如下的一些重要属性

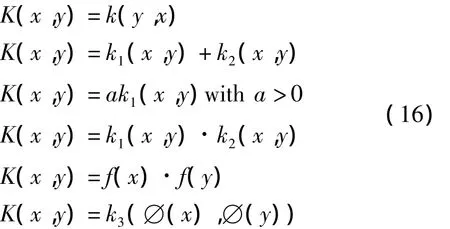
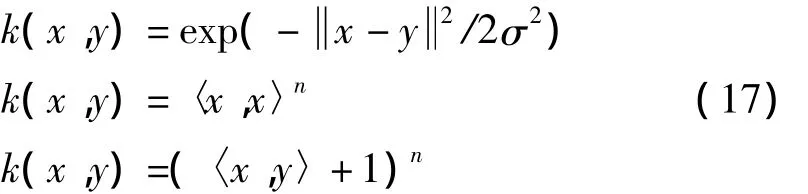
1.4 训练

如前所述，在式(7)的约束下，训练在于寻找w和b。使用式(9)，在式(15)的约束下，训练就是要寻找ai和b。目标是要找到一个最概括的分离平面。必须最大化边界或最小化于是算法训练就变成了式(18)，这是一种有条件的优化。

应用拉格郞日优化理论，式(18)就变成了式(19)［2］。式(19)是一种二次优化问题。二次优化理论表明问题是凸起的，不存在局部最小化问题。在这个优化问题中，通常可以找到最好的结果。这是支持向量机(SVM)的一个重要优势:当给定数据集并选中核心函数后，通常可以找到最好的结果。多次训练这个系统都是得到一个完全相同的结果。虽然二次优化算法有很多种，此处仅介绍支持向量机，更多的信息可以在文献［3］中找到

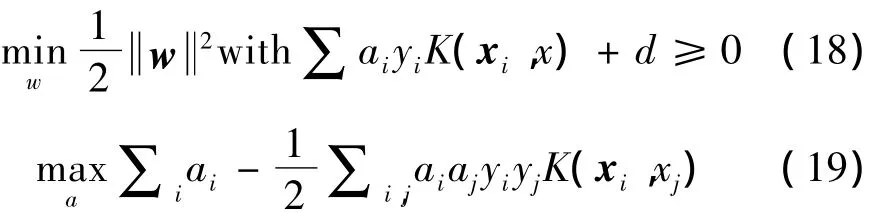
2 短期记忆模型化

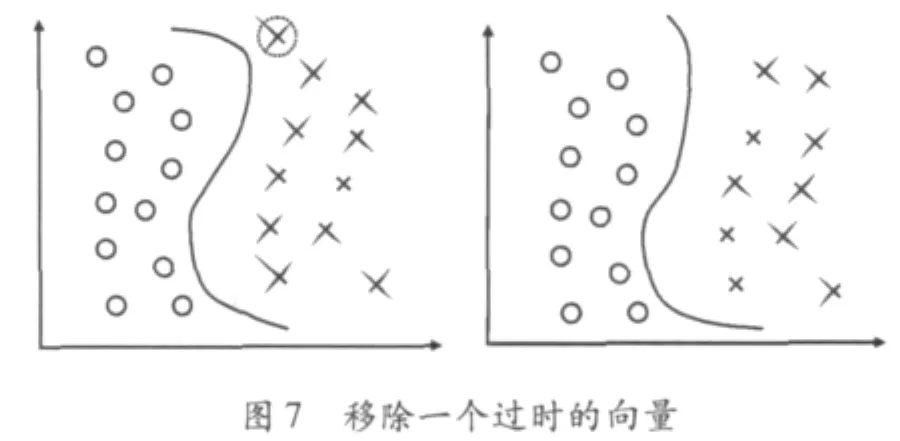
分类器系统是采用收集的数据集进行训练。在一个神经网络中，不可能决定或者知道何时网络忘记过去学到的东西。在支持向量机(SVM)中，分类是支持向量和它们的系数ai来描述的。这些向量是收集到的数据集的一部分。这样就有可能给每个向量标定日期。然后，经过一定的时间段，为取消向量的影响，可以把它从解法集中移走。整个数据集就可以不断地减少最老的向量，增加最新的向量。图7显示了移走一个过时的支持向量时，相应的解法集的变化情况。图8显示了添加一个新的支持向量时，相应的解法集的变化情况。

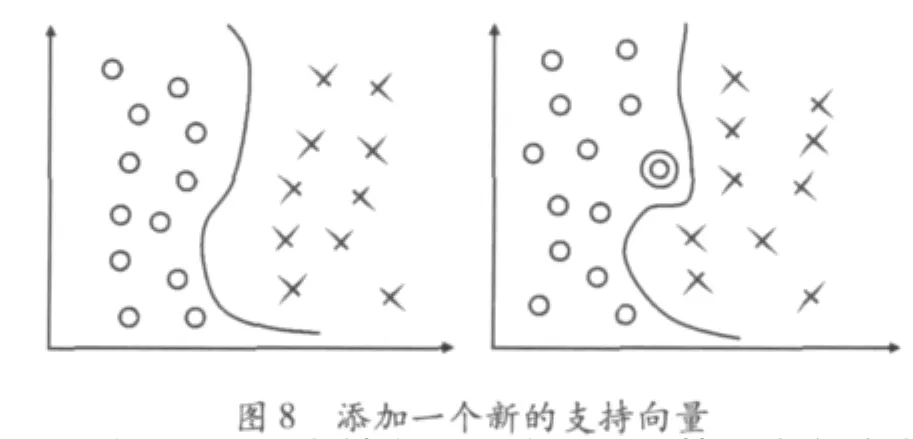
一方面，只要支持向量没有改变，训练就会给出完全一样的结果，解法集也不会改变，并且训练速度也非常快。另外一方面，如果移走一个支持向量，与第一情况相比，训练需要的时间会更长一些，但训练速度也很快，因为非支持向量的数据权重(ai)仍然为零。

系统派生可能会是一个问题，而且除了支持向量和它们的系数ai，解法也受到所选择核心函数的约束。虽然这或许是一个优点，或是一个缺点，因为要选择这样的一个核心就可能会非常棘手。

这种技术在一个充满变化的环境中相当有用，因为过去学习到的知识对现在不会有无止境的影响。对于神经网络，如果环境发生了变化，一些决策可能就不再有效。有时为了纠正这种趋势，会犯多次错误。而对于带有标定日期的支持向量机(SVM)，只会有一次错误或一次长时间的等待。

虽然只在SVM中介绍了这种技术，显然，这种技术也可适用到其他的分类器，只要分类器是从训练数据集中得到的数据来表示它们的参数，例如最邻近算法(KNN，K－Nearest Neighbors)。在加强学习方面，这种SVM可以代替神经网络。

3 CPU的消耗限制

评估点x的值，需要计算方程。这种分类需要计算K(x，y)的值和每个支持向量的两个乘积。重要的是限制分类器对CPU的消耗。降低CPU消耗的唯一方法是限制支持向量的数目，并限制到一个固定值。使用这些带有日期的系统，支持向量数目太高时，最老的支持向量在评估时可以抛开不计。然而，抛开不计的支持向量不能从训练数据集中移走。由此，支持向量必将被另外一个取代。这种行为将会降低分类器的有效性。在游戏中，限制支持向量的数目非常重要，因为它在决策中引入了一些噪音，所以效率下降并非总是坏事

4 结束语

介绍了支持向量机(SVMs)，引出了老化数据的概念。尽管这一概念可以用于大多数的分类器系统，但SVM是个很好的候选者，因为分类器的参数是用训练数据集来表示的，还为支持向量的数量限制和CPU消耗的限制提出了解决方法。

［1］ BURGES C.A tutorial on support vector machines for pattern recognition ［J］.Knowledge Discovery and Data Mining，1998，2(2):955 －974.

［2］ CRISTIANINI N.Tutorial on support vector machines and kernel methods［EB/OL］.(2010 －08 －26)［2011 －12 －19］http://www.support－ vector.net/icml－ tutorial.pdf.

［3］ GOULD N，PHILIPPE T.A quadratic programming page［EB/OL］.(2010－03－17)［2011－12－10］http://www.numerical.rl.ac.uk/qp/qp.html.

［4］ MOORE A W.Support vector machines［EB/OL］.(2009 －09－19)［2011 －12－21］http://www.autonlab.org/trtorial/svm.html.