一种基于复合混沌序列的检材样本图像加密算法
李震
(中国刑警学院 辽宁 沈阳 110035)
一种基于复合混沌序列的检材样本图像加密算法
李震
(中国刑警学院 辽宁 沈阳 110035)
混沌序列具有易生成性,对初始条件强敏感性,可完全重现性,以及整体的伪白噪声统计特性等特点,基于以上特性首先利用复合logistic与Chebyshev映射生成的混沌序列对数字图像位置进行置乱,再次利用logistic映射对彩色图像的RGB值进行加密,从而达到对像素位置和像素色彩域双重加密。软件模拟试验证明该算法实现简单,极大改进图像的直方图分布,算法加密效果良好,安全性高。
图像加密 混沌序列 图像置乱 Logistic映射
随着Internet技术与多媒体技术的飞速发展,数字图像作为多媒体信息中最直观的表达形式,其在网络传输过程中的信息安全性逐渐受到重视。近年来,数字图像混沌加密技术已经成为数字图像加密领域的重要研究领域。许多学者从不同科研角度运用混沌序列的易生成性,对初始条件强敏感性,可完全重现性,以及整体的伪白噪声统计特性等特点设计出多种基于混沌序列的数字图像加密方法,但其中许多算法都是基于一维混沌系统,虽然一维混沌系统具有形式简单,产生混沌序列效率高等特点,但其密钥空间有限,很难有效抵御穷举攻击。
为了克服上述缺陷,本文提出了一种基于混合混沌序列的图像加密算法,首先利用复合logistic与Chebyshev映射生成的混沌序列对数字图像位置进行置乱,再次利用logistic映射对彩色图像的RGB值进行加密,从而达到对像素位置和像素色彩域双重加密。通过实验分析表明,此算法具有可靠、快速和鲁棒性强等特点,并已经应用在公安业务领域中网络会检系统中,从而保证网上会检中案件彩色图片文件传输的安全。
1 混沌映射的分析
混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程,这种过程既非周期,又不收敛,并且对初始值有及其敏感的依赖性。通过混沌映射可以提供数量众多的不相关、可再生的信号,给定一个离散混沌系统两个非常接近的初始值,经过几次迭代后,输出的结果可以完全不相关。因此,利用混沌系统对初始条件的极其敏感的依赖性,可以提供数量众多、非相关、类随机而又确定可再生的混沌序列。当前在混沌系统中,应用较为广泛的一维非线性动力系统主要有Logistic映射与K阶Chebyshev映射。
1.1 Logistic映射及其特性分析
Logistic映射是一种结构简单但应用广泛的一维非线性动力系统,其定义如下:

其中,0≤μ≤4称为分枝参数,Xk∈(0,1)。当3.5699456…≤μ≤4时,Logistic映射工作于混沌状态。也就是说,由初始条件x0在Logistic映射的作用下所产生的序列{Xk},k=0,1,2…是非周期性的、不收敛的,且对初始值非常敏感。对于一般的混沌映射Xk+1=f(Xk),概率密度函数为:

对于式(1)形式的Logistic映射,如果μ=4,Logistic映射所生成的序列的概率分布函数可改写为
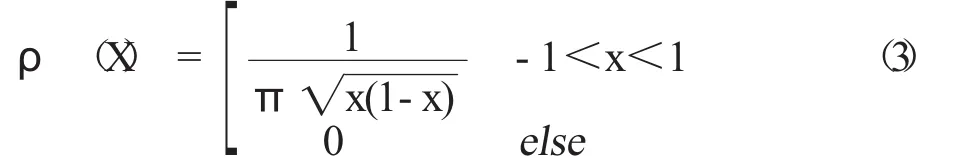
通过ρ(x),可以计算得到Logistic映射所产生的混沌序列的一些很有意义的统计特性。例如,混沌序列轨迹点的均值是

关于相关函数,独立选取两个初始值x0和y0,则序列的相关函数为

Logistic映射的以上特性表明,混沌动力系统具有一定的确定性,其动力统计特性具有形式简单,对初始条件敏感等诸多特性。但是直接通过Logistic映射的迭代所产生的密钥序列有以下缺点:
(1)混沌序列参数μ易被破解。上述由公式生成的混沌序列,无论迭代次数多少,只要可以得到任意一点(Xk,Xk+1),就可确定参数μ=Xk+1/Xk(1-Xk)。
(2)在有限精度下,易陷入周期循环,且周期不易确定,由于在迭代过程中,由于参数μ数值不变,只要产生同样的Xk必将产生同样的Xk+1。计算中由于有限精度效应,Xk只有有限个不同的值,因此必然存在一个迭代周期,此时混沌序列将陷入周期循环中。
1.2 K阶Chebyshev映射及其特性分析
K阶Chebyshev映射是一种简单的参数为阶数的一维混沌映射,其迭代方程为
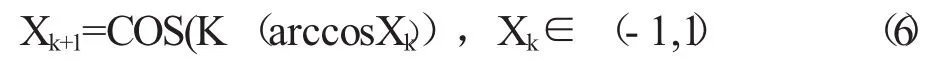
K阶Chebyshev映射生成的混沌序列的概率密度函数为

通过ρ(X),可以得到Chebyshev映射的混沌序列的统计特性。例如,混沌序列轨迹点的均值是

关于相关函数,独立选取两个初始值x0和y0,则序列的相关函数为
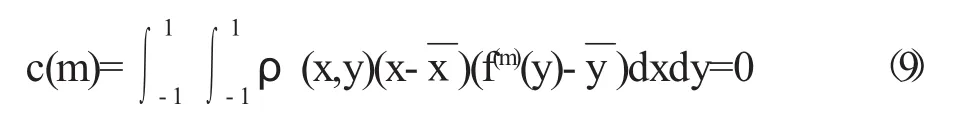
K阶Chebyshev映射的以上特性表明,混沌动力系统具有一定的确定性,其动力统计特性具有形式简单,对初始条件敏感等诸多特性。
1.3 混沌序列的生成
为避免Logistic映射生成混沌序列参数μ易被破解和陷入周期循环的缺陷,提高混沌的复杂性、本文对混沌映射进行改进,采用Chebyshev映射的迭代输出的混沌序列作为Logistic映射的控制参数,使Logistic映射的控制参数μ也同样处于混沌状态,增加μ的变化情况,避免出现周期循环,可以增加算法的密钥空间,提高算法的抗攻击能力。生成的混沌序列的具体方法如下:
(1)实数序列:将Chebyshev映射阶数k,初始值x0,代入(6)式中输出混沌序列{Xk,k=0,1,2,… },由于Logistic映射与k阶Chebyshev映射在方程的定义值域存在较大差异,可采用线性分段函数将生成的Chebyshev映射混沌序列{Xk,k=0,1,2,… }转化到3.5699456…≤μ≤4的值域范围内,形成序列{μk,k=0,1,2,… },将|Xk|,μk代入(1) 式中形成实数序列。
(2)比特序列:由上述的实数值混沌序列得到,比特序列是通过对{μk,k=0,1,2,… }中的μk改写为L-bit的浮点数形式得到的。
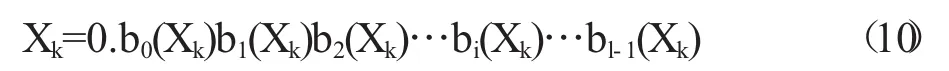
其中bi(Xk)是Xk的第i位。所需数列即为:
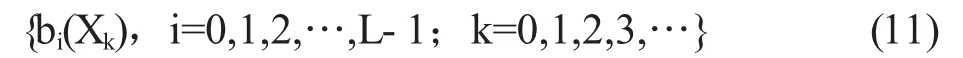
2 基于复合混沌序列的彩色图像加密算法
2.1 算法原理
彩色数字图像通常都是由矩阵Am×n保存,每个矩阵元素ai,j的值表示彩色图像对应像素的RGB值以及Alpha(透明度)值,本算法首先采用对Am×n进行数学变换,对原始彩色图像各个像素点位置进行置乱,即将原始图像矩阵Am×n转化为Bm×n,破坏原图像的有序性,达到置乱的目的,从而实现对像素位置的加密,再利用复合比特混沌序列对Bm×n进行像素值的变换,即通过转化复合比特混沌序列,对Bm×n中的每一个元素bi,j的像素值进行加密,改变密图的R、G、B值,甚至改变Alpha(透明度)值,具体的加密算法如图1所示,表示彩色数字图像的矩阵中对应的每一个元素值都是由32位4个字节构成,其具体的存储结构如图2所示。

图1 基于复合混沌序列的彩色图像加密算法的流程图

图2 彩色数字图像像素点的构成
通过加密算法对对每一个像素的32位进行加密,彻底改变彩色图像的像素值,将像素位置置乱和像素值置换的双重加密技术可以大大提高加密算法的抗攻击性。
2.2 加密与解密算法设计
基于复合混沌序列的彩色图像加密算法设计基于Logistic映射和Chebyshev映射,算法的密钥参数为Chebyshev映射的阶数k和初始值x0。设原始图像为A(i,j),i=0,1,2,…M-1,j=0,1,2,…N-1。其中(i,j)表示为某一像素的坐标,g(i,j)表示该像素点的RGB和Alpha值。彩色图像的具体加密过程如下:
(1)利用Chebyshev映射的阶数k和初始值x0,采用式(6)生成混沌序列{Xk,k=0,1,2,…M×N-1},采用线性分段函数将生成的Chebyshev映射混沌序列{xk,k=0,1,2,… M×N-1}}映射至3.5699456…≤μ≤4的值域范围内,形成序列{μk,k=0,1,2,…MN-1 },将|Xk|,μk代入(1)式中形成实数序列。取初始值x0=0.123,k=6,同时为了增加算法的随机性,不使用该序列的初始段部分,由Logistic映射产生一个长度为MN的实数混沌序列L{L1,L2,…LM×N}。
(2)将生成的实数混沌序列转化为二维矩阵LM×N,并与原始图像AM×N中的元素一一对应。对二维矩阵LM×N从第1行至第M行,同行N个元素进行排序,形成每行都是有序的二维矩阵L′M×N,由于原始图像AM×N的每个元素位置与二维矩阵LM×N每个元素一一对应,原始图像AM×N转化为A′M×N。同理,再对二维矩阵L′M×N从第1列至第N列,同列M个元素进行排序,形成每列都是有序的二维矩阵L"M×N,AM×N转化成A"M×N,即完成彩色图像的位置置乱,形成像素位置置乱的密图BM×N。
(3) 重复步骤(1) 中,取初始值x1=0.156,k′=6,同时为了增加算法的随机性,不使用该序列的初始段部分,由Logistic映射最终产生一个长度为4×M×N的实数混沌序列L{L1,L2,…L4×M×N},将生成的实数混沌序列按公式(12)转化成比特混沌序列P{P1,P2…P4×M×N}其中i=1,2… 4×M×N

(4) 生成的比特混沌序列P{P1,P2…P2×M×N},每四个元素构成一维数组,比特混沌序列P转化为二维矩阵P′M×N,其中元素是由比特混沌序列数组P′{P1′,P2′… PM×N′}组成。P1′={P4i+1,P4i+2,P4i+3,P4i+4},i=0,1,2… M×N-1。
(5) 将BM×N的元素bi,j的R、G、B、Alpha分量分别进行像素值加密,具体的方法是将bi,j的R、G、B、Alpha分量分别与Pi′数组中的4个分量,Pi′{P4i+1,P4i+2,P4i+3,P4i+4}进行按位异或。由此得到数字图像加密矩阵CM×N,即是经过像素位置置乱与像素值加密后的密图。
解密过程与加密过程互逆,先将密图CM×N经过像素值比特混沌序列解密得到密图BM×N,最后将BM×N经过像素位置置乱的混沌解密,先按列解密再按行解密,得到数字图像Am×n,完成解密。解密算法的步骤顺序与加密算法顺序依次颠倒,各阶段生成的混沌序列的初始值都不变。
3 实验结果与分析
3.1 实验结果
笔者在vc#.net实现上述算法,并采用本文算法针对多幅图像进行加密,实验中所用的原始图片为如图3(a)所示的256×256彩色印章印文图片,取初始值(密钥)x0=0.124,阶数k=6.0,图3(b)为采用本文复合混沌序列算法所得到的加密图像。图3(c)为密钥正确的解密后的图像,图3(d)为密钥错误的解密后的图像。从仿真实验结果来看,本算法能有效的加密和解密图像,如初始值(密钥) x0=0.125,阶数k=6.0,就无法对图像进行正确解密。

图3 仿真实验结果
3.2 灰度直方图分析
由于图像的连续性,其像素分布是不均衡,因此可以针对这一特殊情况进行统计攻击。图4(a)和图4(b)相比较,可见使用本算法的加密密图的直方图分布很均匀,完全掩盖了变换前的分布规律。

图4 印章印文图像加密前后的灰度直方图
3.3 密钥敏感性分析
密钥敏感度主要分析在加密一幅图像后,采用不同的密钥进行解密实验中,检测其是否可以还原出正确的加密图像。错误密码解密如图3(d)可以看到加密密钥和解密密钥相差千分之一,也不能正确解
3.4 密钥空间分析
基于复合混沌序列的图像加密算法的密钥参数为Chebyshev映射的初态取值空间为(-1,1),在计算机仿真实验中,其初态是由64位数表示,穷解法破解空间巨大,该算法明显可以抵抗穷解法的攻击。
3.5 两相邻像素点的相关性分析
首先从图像中随机选取3000对相邻像素点,然后利用以下公式计算:
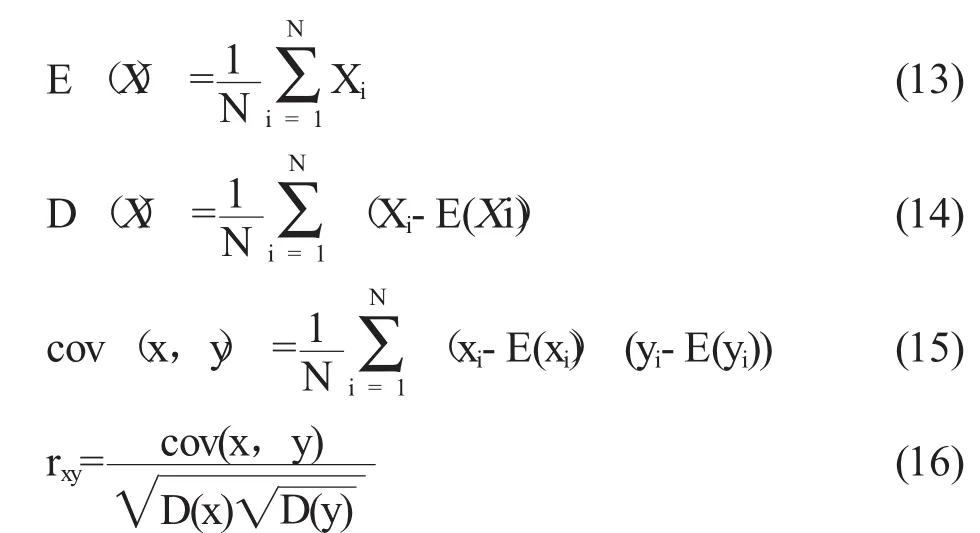
式中,x和y分别表示图像中2个相邻像素的灰度值,rxy即为2个像素点的相关系数,统计结果表明印章印文图像的原相邻像素高度相关,其相关系数接近1,经过文本加密算法加密后的密图,其相邻像素的相关系数接近0,这说明密图的相邻像素已经基本不相关,表明本算法具有较强的抗统计分析能力。
4 结论
提出了一种基于复合混沌序列的彩色图像加密算法,该算法基于Logistic映射和Chebyshev映射,采用线性函数将由Chebyshev映射生成的混沌序列转化至logistic映射的μ的值域范围内,并将由此生成的 Logistic映射的分枝参数 μ 的实数序列和由Chebyshev映射生成的混沌序列生成的初始值对彩色图像进行像素位置置乱,再利用生成的比特混沌序列对像素位置置乱后的密图中的像素RGB和Alpha值进行加密。仿真实验表明由于利用复合混沌序列对像素位置和像素值的双重加密,算法的密钥空间大,对初始密钥极端敏感,直方图分布均匀,加密效果良好,加密速度快,具有极高的安全性,该算法现已应用于公安业务领域中网络会检系统中,有力地保证网上会检工作中有关案件的彩色图片文件传输的安全。
1.管春阳,高飞.一种基于混沌序列的加密算法[J].北京理工大学学报,2003,23,(3)
2.易开祥,孙鑫,石教英.一种基于混沌序列的图像加密算法[J].计算机辅助设计与图形学报,2000,12,(9)
3.闫伟齐,邹建成,齐东旭.一种基于DES的数字图像置乱新方法[J].北方工业大学学报,2002,14,(1)
4.丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,13,(4)
5.徐全生,李震,杜旭强.一种基于混沌序列的图像加密算法[J].小型微型计算机系统,2006,27,(9)
6.金晨辉,高海英.对两个基于混沌的序列密码算法的分析[J].电子学报,2004,34,(7)
7.陈永红,黄席樾.基于混沌序列的图像加解密算法[J].计算机工程,2004,30,(21)
8.高飞.一种新的图像加密算法[J].计算机工程与设计,2007,28,(9)
9.Huang C K,Nien H H.Multi chaotic system based pixel shuffle for image encryption[J] .Optic Communications,2009,282,(11)
10.Fridrich J.Symmetric ciphers based on chaotic maps[J].SystemsManandCybernetics,Computational CyberneticsandSimulation,1997,2,(1)
11.Habutsu.A secret key cryptosystem iterating a chaoticmap[J].Eurocrypt,1991.
12.Rhouma R,MeherziS,BelghithS.OCMLBased Colour image encryption[J].Chaos, Solution &Fractals,2009,40,(1)
13.Alvarez E,Fernondez A,Garcia P,etal.New approach to chaotic maps[J].Int J Bifurc Chaos,1998,8,(6)
14.FreyD R.Chaoticdigitalencoding:Anapproach to secure communication[J].IEEE Transaction on CircuitsandSystems,1993,40
15.Pareek N K,Vinod Patidar,Sud K K.Image encryptionusingchaoticlogisticmap[J].ImageandVision Computing,2006,24
16.Nikolaidis A,Pitas I.Region-based image watermarking[J].IEEE Transactions on Image Processing,2001,10,(11)

