基于健康监测系统斜拉桥有限元模型修正的实现

方冬慧，晁忠贵，王清远

(1.四川大学锦城学院土木与建筑工程系，四川 成都 611731;2.攀枝花市建设工程质量安全监督站，四川 攀枝花 617000;3.四川大学建筑与环境学院，四川 成都 610065)

大跨度桥梁具有柔性大、频率低，易受环境温度、湿度的影响，以及长期承受动力荷载等特点，因此结构的安全性和耐久性是一个值得特别关注的问题。而对大桥建立结构健康监测系统是有效的解决方法［1］～［3］。其目的是通过对大桥在各种荷载以及环境因素作用下的结构形态进行实时监测和研究，评估其安全性、适用性和耐久性，为大桥的运营管理、养护维修提供依据和科学的指导。

本文以深圳湾公路大桥斜拉桥为工程背景，采用健康监测系统提供的数据获得斜拉桥的模态参数。在分析设计变量对模态参数变化的灵敏度特性的基础上对建立的有限元模型进行修正，比较快速有效地得到了能够反映大桥动力特性的基准有限元模型，为大桥的健康监测和损失预警的研究提供了基础。所涉及的主要技术有灵敏度分析、模态参数识别、优化计算方法。

(1)利用健康监测系统提供的拉索振动数据，通过振动法获得斜拉索的基频，从而求出索力作为有限元模型的输入参数;

(2)利用随机减量/ITD法对布置在桥塔和钢箱梁上的加速度传感器实测加速度信号进行处理，获得大桥的模态参数;

(3)设计参数的灵敏度分析，将桥塔和钢箱梁分为25部分，选择对动力性能影响比较大的两个参数(材料弹性模量和密度)对大桥进行基于动态特性的灵敏度分析，最终确定修正部位及对斜拉桥的有限元模型进行了修正。

1 工程背景

深港西部通道深圳湾公路大桥(图1)是连接大陆深圳和香港的跨海大桥，由深圳方和香港方共建。该桥全长5545 m，其中深圳侧总长2040 m。桥梁深圳部分和香港部分的分界线在深圳侧非通航孔引13#桥墩位置。大桥为双向六车道，设计行车速度为100km/h，全桥总宽度为38.6 m。深圳侧大桥包括换道立交、通航孔桥和非通航孔桥。本文主要研究的对象是通航孔桥，因此下文中提到的深圳湾公路大桥(SZWB)也均属通航孔桥。主1#墩为主桥起点，桩号为ZK0+000.000。

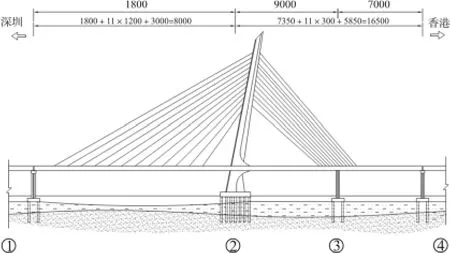
图1 深圳湾公路大桥立面(单位:m)

2 振动法测定索力

斜拉索是斜拉桥的主要受力构件，索力的变化是衡量斜拉桥是否处于正常营运状态的重要标志，因此索力的精确测量十分必要。深圳湾大桥安装有17个压力传感器直接测定索力，另安装12个加速度传感器，通过傅立叶分析技术的频率法可以间接测定索力［4］。将5根同时安装有索力计和加速度计的斜拉索分别得到的索力作对比分析，验证了频率法的准确性。并结合直接法和间接法计算出全桥24根拉索的索力。

频率是影响索力测试精度的一个重要影响因素。为了从拉索的实测加速度时程响应中提取精确的频率，本文利用matlab语言，编制了相应的计算程序，对时程响应曲线进行了消除趋势项、信号加窗并对比了不同窗函数的计算结果，最后求取了响应信号的自功率谱，提取了斜拉索的固有频率。图2为S03号拉索的自功率谱曲线。

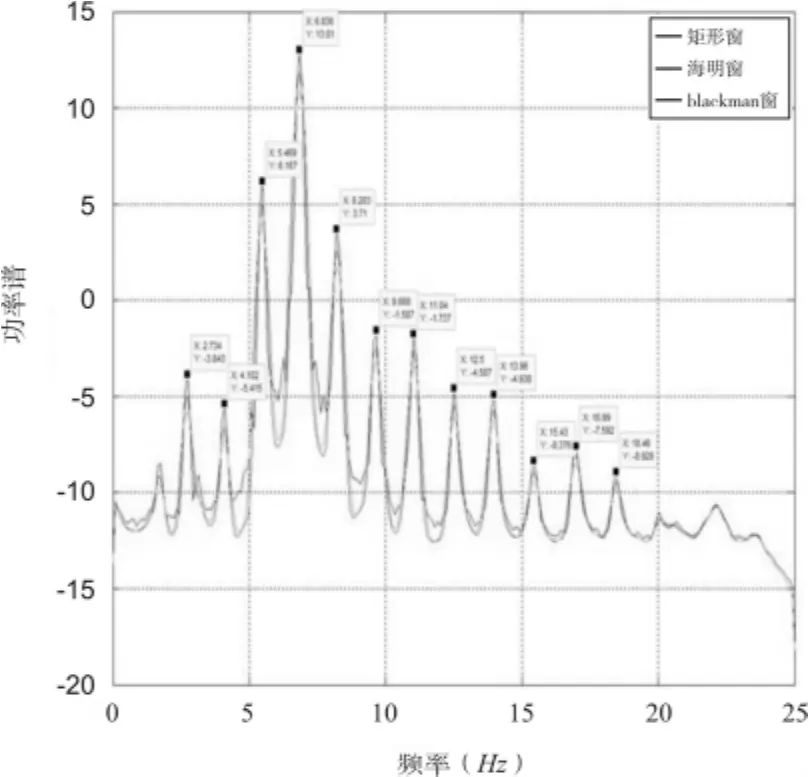
图2 S03索在不同窗函数下的功率谱曲线

从图2看出，不同窗函数下计算的功率谱曲线的峰值点基本相同，所求基频即为各相邻峰值间距的平均值，得知S03索的基频f=1.4296 Hz。因此可推算出S03索的索力:T=6068.4 kN。同理可求出其余拉索的索力，与直接测试得到的索力对比结果如图3示。

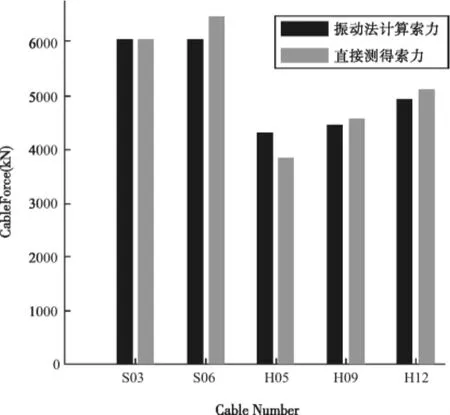
图3 两种测试方法的索力比较

振动法作为一种由频率间接换算索力的方法，关键问题在于如何由实测数据得到正确的拉索频率值。通过对5根拉索的索力比较，索力大小误差均在5.0%以内，可见利用振动法测定索力精度较高，结果可靠。全部索力计算结果如表1所示。

表1 利用振动法测得的索力结果

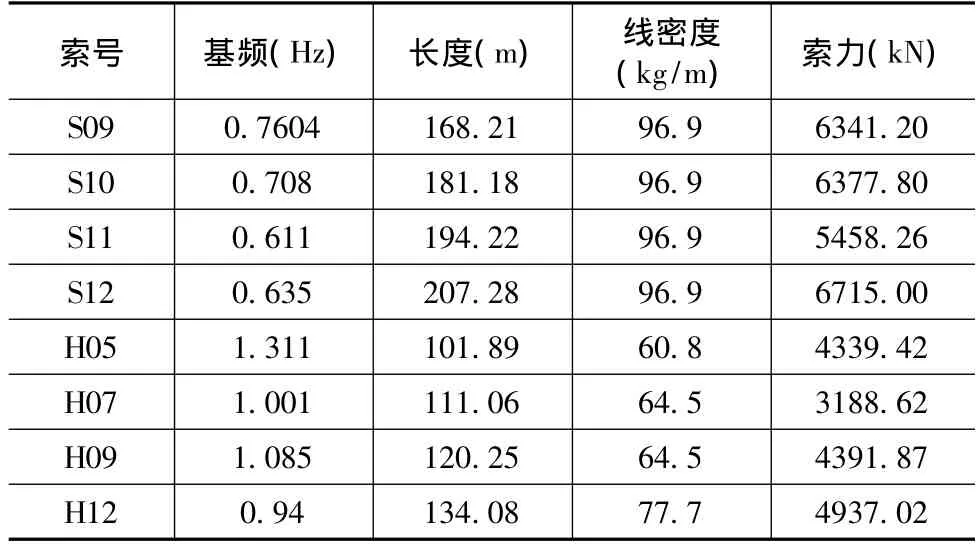
续表1

3 模态参数识别

试验模态参数识别是振动信号处理的一个重要部分，其主要任务是从测试获得的振动信号数据中确定振动系统的模态参数。本文利用随机减量/ITD法识别了深圳湾大桥的模态频率［5］，以10 min为单位连续进行了模态参数识别，24 h内可以得到144个实测模态频率。图4～图7给出了2009年10月1日识别出的前10阶模态频率的日变化曲线，将其平均值作为识别模态频率。

图4 第一阶频率变化趋势

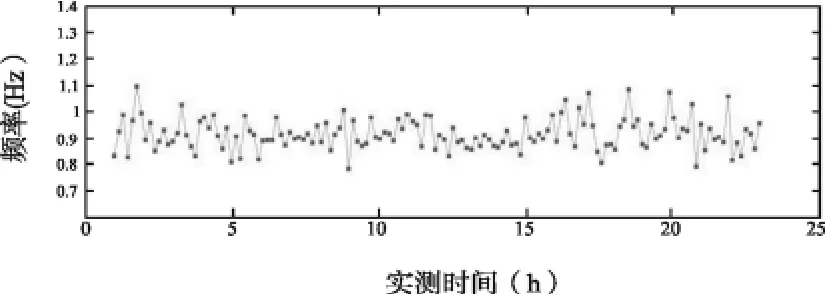
图5 第二阶频率变化趋势

图6 第三阶频率变化趋势

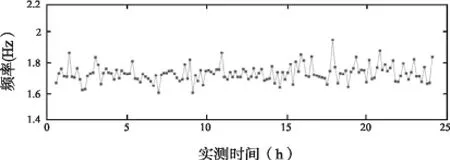
图7 第四阶频率变化趋势

4 有限元分析

有限元建模中采用ANSYS提供的以下三种单元类型:(1)空间梁单元BEAM188，用于模拟桥面钢箱梁、横隔板和桥塔;(2)空间杆单元LINK10，用于模拟与塔梁相连接的斜拉索;(3)空间质量单元MASS21，用于模拟桥面铺装和附属设施以及3号墩附近的混凝土压块。选用“鱼脊”模型建立空间杆系有限元，全桥共计230个梁单元，24个杆单元，32个质量单元。

本文采用分块索兰法对深圳湾大桥进行了模态分析，其前10阶自振频率和振型见表2。可得:(1)该桥基本周期为2.916 s，符合独塔斜拉桥的短周期特点;(2)主振型为桥塔侧弯，这种振型正好符合单索面斜拉桥的特征;(3)第二、三阶振型为主梁竖向弯曲，因为低阶振型对结构反应贡献很大，可知主梁的竖向弯矩和位移较大。因此，可认为计算结果是比较精准的。

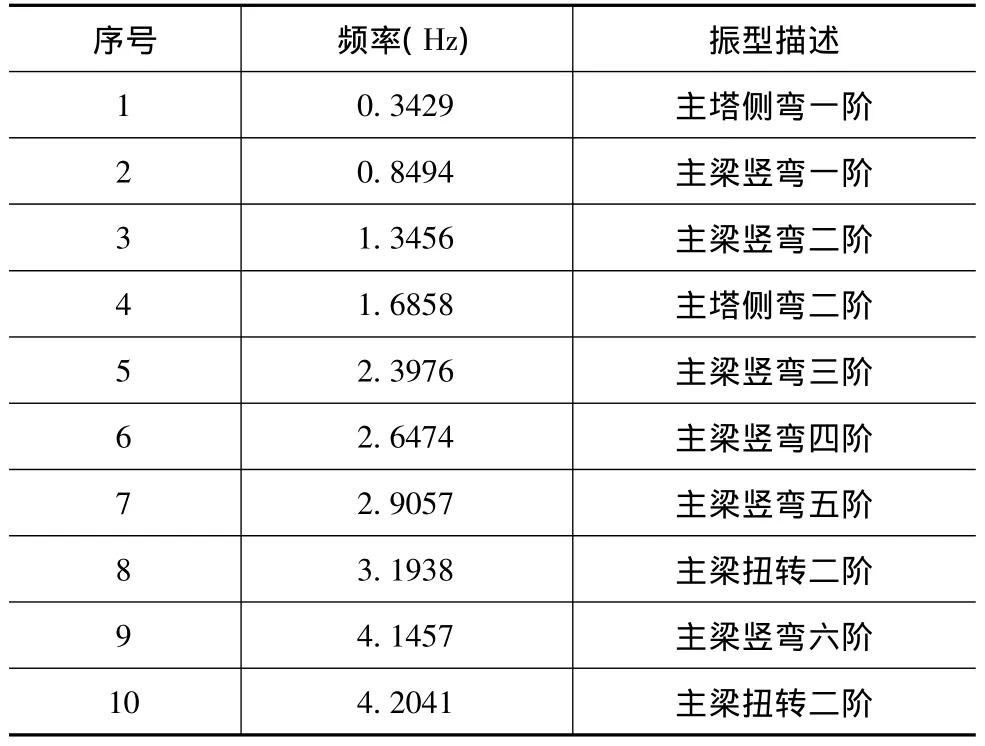
表2 深圳湾大桥的动力特性(有限元计算结果)

将健康监测系统数据分析所得桥面系的自振频率与有限元计算所得的桥面系的自振频率作对比分析，其结果见表3。

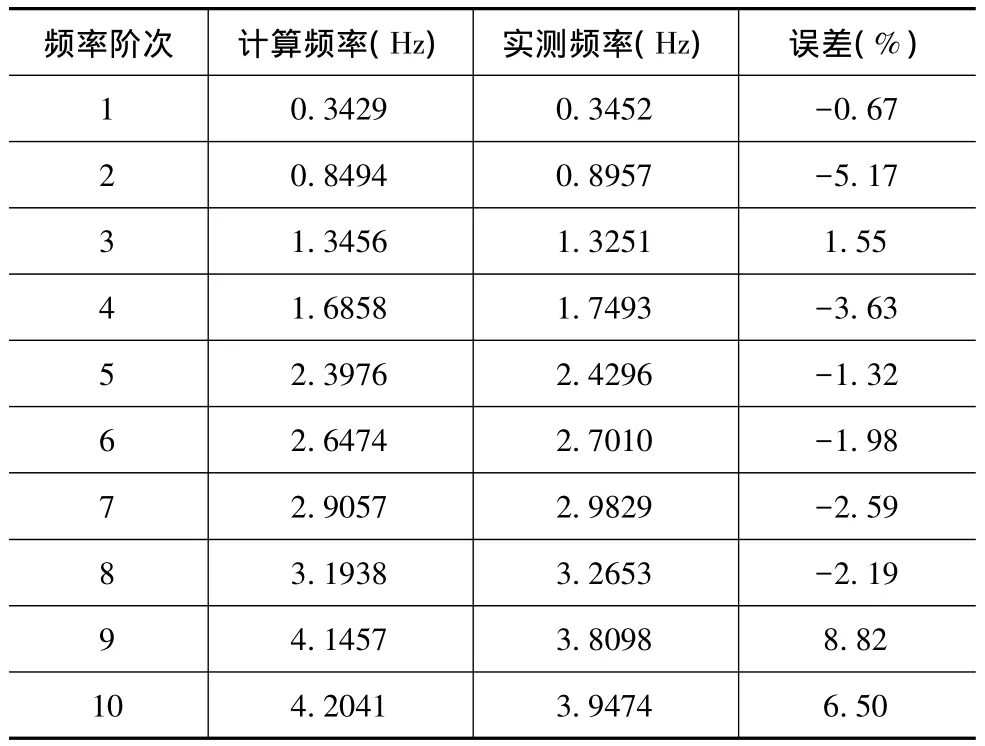
表3 大桥自振频率对比表

从表3可见，实测结果与理论计算结果比较，二者振型顺序相同，频率值比较接近，最大差值在第9阶，为8.82%。

5 灵敏度分析

修正参数的合理选择，对于有限元模型修正的成功起着关键的作用［6］。灵敏度的分析一般是采用直接求导的方式。直接求导法是将特征值和特征向量视为结构参数的多元函数，直接对其求导而得出的某一参数目标函数的灵敏度函数。

影响结构动力特性的参数多为结构刚度、材料密度、结构尺寸误差等［8］。相对主梁和拉索，斜拉桥索塔结构刚度很大，在全桥有限元模型中，索塔结构刚度、质量等参数的准确模拟、单元划分的合理对全桥结构的静、动力分析的准确性起着至关重要的作用，因此选择桥塔材料和几何尺寸作为修正参数。钢箱梁由于结构加工工艺较为成熟，工厂制作条件优越，因此，在尺寸方面存在的误差较小，主要是桥面铺装重量和钢箱梁刚度的理论值和实际值之间存在一定的出入。

综上所述，在此选取索塔材料弹性模量Etower、密度ρtower、钢箱梁弹性模量Ebeam、密度ρbeam为结构参数，根据塔柱构造将桥塔从底到顶分成5个部分;将钢箱梁分成20个部分;ZK0+000.000～ZK0+180.000每隔18 m为一个部分;ZK0+180.000～ZK0+345.000每隔16.5 m为一个部分。修正考虑的参数共有(20+5)×2=50个。将4个结构参数分别改变0.1倍时对大桥模型结构动力特性的影响如图8的特征值灵敏度矩阵。修正参数的顺序为:桥塔的弹性模量→桥塔的密度→钢箱梁的弹性模量→钢箱梁的密度。

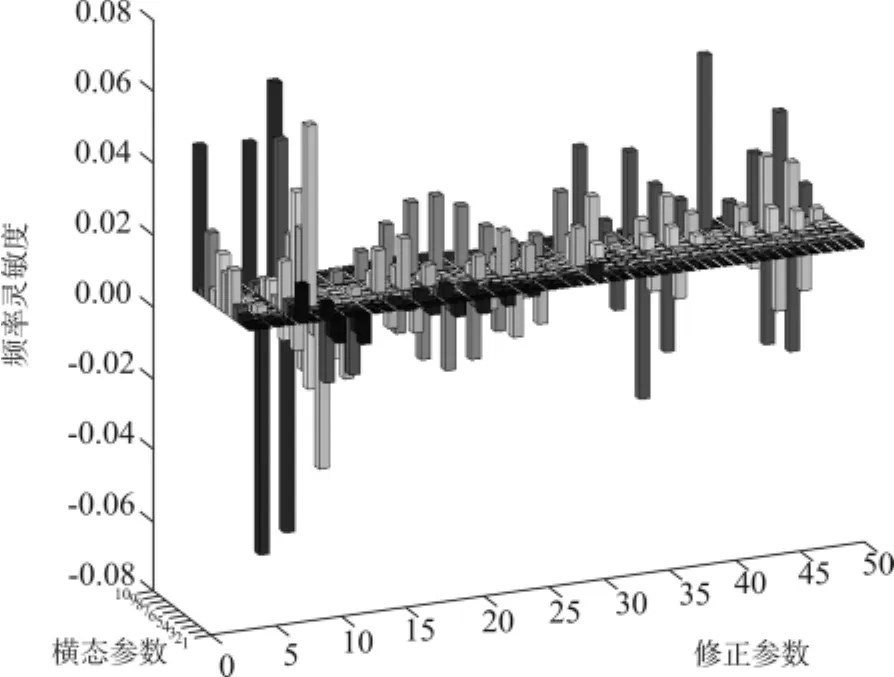
图8 修正参数对频率的灵敏度矩阵

由以上灵敏度分析结果可见，绝大部分参数对大桥的高阶频率均有影响，某些参数(例如塔柱的弹性模量E)对所有的频率都有较大的影响，而另外一些参数(例如塔柱的密度ρ)则影响较小。从图8中还可看出，中塔柱对低阶和第10阶频率的灵敏度较大，钢箱梁弹性模量和密度在桩号ZK0+072.000～ZK0+144.000对第9阶频率影响较大，因此在模型修正时采取这些为修正变量。

6 修正结果

将有限元模型计算得到的前10阶固有频率fc与实际的前10阶测试频率fc的误差平方和作为目标函数，并将前10阶固有频率 fc作为状态变量，其变化范围为0.9fc≤f≤1.1fc，将灵敏度分析的结果作为设计变量，其值的变化范围为建模值的0.8～1.05倍，运用ANSYS软件的优化方法进行优化迭代［7］，最后得到较为精确的有限元模型。

修正后的结果如表4所示。

表4 修正后的自振频率对比表

从表4中可见，修正结果与实测计算结果的频率比较接近，最大差值在第10阶，为5.355%。从灵敏度特性矩阵可知，设计变量的小幅度变化导致的频率变化不大，因此若想得到更精确的结果只有扩大设计变量的变化范围。

7 结束语

(1)在使用振动法测试索力时，直接使用FFT变换和加窗平均周期法，而且利用加窗平均周期法时不同的窗函数对索的基频的识别结果无影响，均可准确测得索的基频。

(2)模型修正时设计变量、状态变量的选择和变化范围对修正结果的效率和修正结果的影响较大，本文在分析设计变量可能的变化之后提出了大致的变化范围，其修正目标明确，修正结果也较满意。修正后的模型可作为结果的基准有限元模型，用于结构的其它分析。

(3)无论从拉索索力的识别还是模态参数的识别，都是基于健康监测系统数据的处理，因此为健康监测海量数据库的处理提供了一种很好的思路。

［1］李宏男，高东伟，伊延华.土木工程结构健康监测系统的研究状况与进展［J］.力学进展，2008(2)

［2］范立础，袁万城，张启伟.悬索桥结构基于敏感性分析的动力有限元模型修正［J］.土木工程学报，2000(1)

［3］Wang Hao，Li Aiqun，Miao Changqing.Finite element model updating and validating of Runyang Suspension Bridge based on SHMS［J］.Journal of Southeast University，2005

［4］陈刚，任伟新.基于环境振动的斜拉桥拉索基频识别［J］.地震工程与工程振动，2003(3)

［5］谢献忠，陈文新，钟新谷，等.环境激励下湘潭莲城大桥模态参数识别研究［J］.湖南科技大学学报(自然科学版)，2008(4)

［6］袁爱民.基于灵敏度分析的有限元模型修正技术若干关键问题研究［D］.东南大学，2006

［7］李效法.基于灵敏度分析的模型修正研究及其实现［D］.南京航空航天大学，2007

［8］秦仙蓉.基于灵敏度分析的结构计算模型修正技术及其相关问题研究［D］.南京航空航天大学，2001