大型客车门窗口变形分析与优化*
高云凯 田林雳 汪 翼 徐宸原
(1.同济大学;2.山东大学)
1 前言
车身开口变形过大会影响车身密封性,导致漏水等现象,严重时可能出现挡风玻璃扭碎或车门卡死等现象,所以在进行车身结构设计时要满足实际使用工况对车身开口变形量的要求。
本文利用MSC.Nastran软件求解得到了某大型客车的结构性能参数,发现其门窗对角线变形量偏大,扭转刚度偏小,有必要进行结构优化设计。基于灵敏度分析筛选出部分梁截面尺寸作为优化设计变量,约束门窗对角线变形量和单元应力,以轻量化为目标,采用MSC.Nastran优化模块对门窗口变形进行了优化,根据优化结果修改结构并进行了验证。
2 有限元分析
2.1 有限元模型
客车车身有限元建模时,车身骨架采用梁单元模拟,而车身骨架间焊接板件、车身加强板及地板搁栅等板件采用板壳单元模拟,异形钢管之间的焊接用RBE2模拟。
有限元模型采用基本单元尺寸为50 mm的BAR单元,骨架间焊接板离散化时采用基本单元尺寸为50 mm的SHELL单元,材料都为钢,密度为7.85×10-9mm3/t,弹性模量为 210 GPa,泊松比为 0.3。模型中的节点总数、单元总数和RBE2单元数分别为19441、21451和2787。用于模态分析的车身骨架梁单元模型如图1所示。
2.2 模态分析结果
在空载模型基础上,不加任何约束与载荷,用Block Lanczos方法分析车身骨架梁模型的自由-自由模态。用Nastran软件求解,采用模态法提取0~60 Hz内的结构模态结果如表1所列。
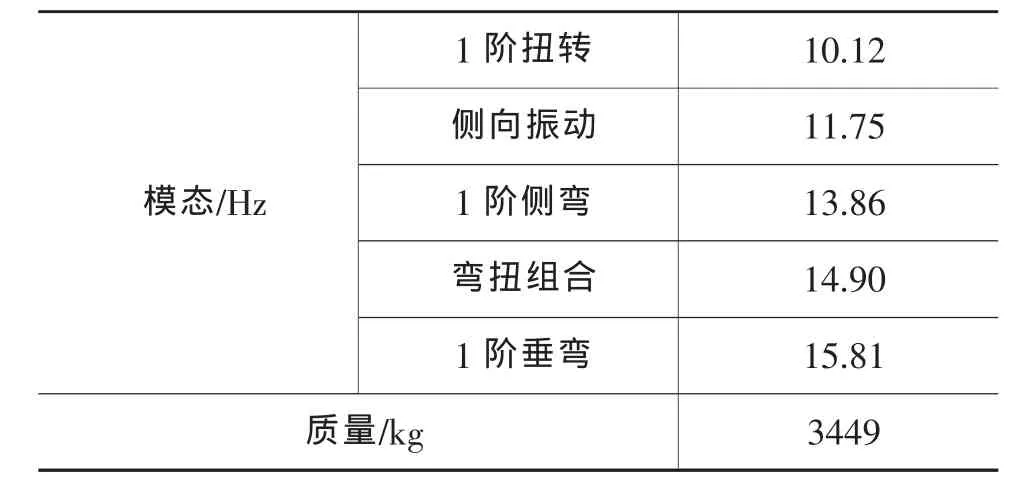
表1 车身骨架结构模态结果
参考有关文献,12m大型客车车身骨架的低阶弹性模态可归纳为[3,4]:1阶扭转模态频率范围在8~10 Hz之间,1阶弯曲模态频率范围在11~20 Hz之间。由表1可知,该大型客车骨架结构的动态振动特性合理。
2.3 刚度分析结果
静态工况考虑满载弯曲、1轮悬空和试验扭转工况来模拟客车的实际使用工况。满载弯曲工况考虑2.5倍动载系数,1轮悬空工况考虑1.5倍动载系数。
试验扭转工况的边界条件如下:
载荷:乘客以每人65 kg计算,将人和座椅的质量等效成集中载荷或均匀分布集中载荷,将发动机及变速器、空调车顶组件、天然气瓶组、蓄电池组等部件的质量等效为集中载荷。
约束:采取前轮悬空后轮约束的方法。前部T型加载梁中点约束x、y、z 3个移动自由度和绕y、z两个方向的转动自由度,后钢板弹簧前、后吊耳处约束全部6个自由度。
根据轿车台架试验标准,并参考文献[1]计算得到该大型客车试验扭转刚度为 39 614.1 N·m/(°)。根据统计资料,国产半承载式客车扭转刚度在20 000~64 000 N·m/(°)范围内[2],可知本文所研究车型的扭转刚度处在合理范围内,但与同类车型相比还处于偏低水平。
对大型客车而言,车身开口变形主要指门窗口变形,由于其侧窗较多且变形较小,本文主要对前风窗、前门框和中门框的对角线变形量进行了分析。计算得到静态工况下门窗对角线变形量如表2所列。
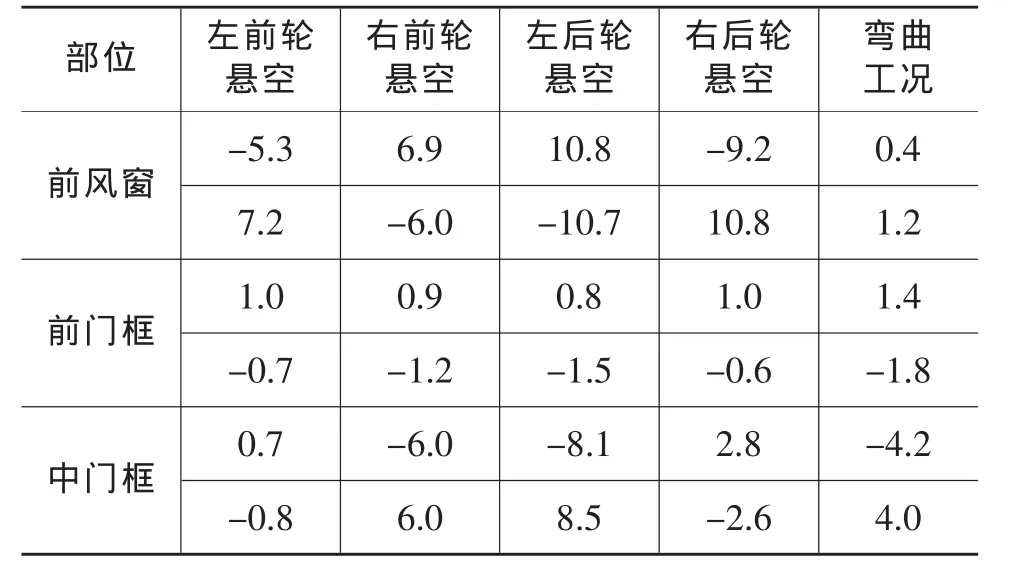
表2 各静态工况门窗对角线变形量 mm
由表2可知,在弯曲工况下,门窗对角线变形量都满足“门窗框对角线变形量不得超过5 mm”的要求[3];在1轮悬空工况下,前风窗和中门框的对角线变形量都有超过5 mm的情况,后轮悬空工况最大变形量甚至达到10.8 mm,说明前风窗和中门框刚度不足。在各种工况下前门框的变形量都较小,远小于5 mm,说明前门框的刚度充裕,存在优化空间。因此,对于刚度不足的前风窗和中门框需进行结构改进设计,对于刚度充裕的前门框可进行结构优化设计以提升性能。
3 结构优化
3.1 优化思路
本次优化的主要目标是控制静态工况下门窗对角线的变形量,提高车身结构刚度。同时考虑结构轻量化的要求,在质量不增加或质量增加最少的前提下获得结构刚度的最大提高。为此以结构轻量化为目标函数,以门窗框对角线变形量不超过5mm为约束条件,进行梁截面尺寸优化。优化求解流程如图2所示。
3.2 灵敏度分析与设计变量选取
建立了大型客车梁单元模型,选择车身梁截面尺寸为设计变量。由于大型客车车身空间梁结构复杂,由此建立的设计变量多达358个,为了提高优化效率,需要进行结构灵敏度分析,以筛选出部分梁截面尺寸作为优化设计变量。
本文重点分析左后轮悬空、右后轮悬空工况下前风窗和中门框对角线变形量对梁截面尺寸的灵敏度。
约束前风窗、中门框对角线变形量不超过5 mm,以车身骨架质量最轻作为目标函数,提交Nastran求解输出各响应相对于设计变量的灵敏度系数矩阵。
车身质量相对于设计变量的灵敏度用符号Sm表示,前风窗对角线变形量和中门框对角线变形量相对于设计变量的灵敏度分别用符号Sw、Sd表示。引入相对灵敏度指标Sw/Sm和Sd/Sm,当该比值小于0时,绝对值越大,表示减小等量的对角线变形量所需增加的质量越小;当该比值大于0时,绝对值越大,表示减少相同质量导致的对角线变形量增加值越大[2]。在优化时应优先选用Sw/Sm和Sd/Sm绝对值都大的设计变量。
根据上述准则,筛选得到的设计变量在车身骨架结构中的分布如图4所示。
由图4可知,窗立柱、侧围斜撑、侧围裙梁、顶盖横梁,以及前风窗上、下横梁和前围外框等结构对门窗变形量较为敏感,选择这些梁截面作为设计变量进行尺寸优化,能在车身质量不增加或增加最少的情况下实现结构刚度的最大提高。
3.3 门窗口变形优化
本次优化考虑弯曲和1轮悬空共5个工况,设计变量为经上述灵敏度分析筛选出来的50个设计变量,约束门窗对角线变形量不超过5 mm以及各单元应力不超过235 MPa[4],以车身骨架的质量最轻作为目标函数。
经过18次迭代优化后达到硬收敛,目标函数迭代历程如图5所示。
由图5可知,车身骨架质量由优化前的3 449 kg增加到优化后的3 455 kg,质量增加6 kg。
为了使优化后的截面尺寸能够为生产实际所采用,对优化后的结果进行圆整。圆整后尺寸增大和减小的设计变量在车身结构中的分布情况如图6和图7所示。
由图6和图7可知,优化后尺寸增大的设计变量主要集中在中门框和前围,尺寸减小的设计变量主要是顶盖横梁、窗立柱和侧围斜撑等结构。
4 优化前、后结构性能对比
优化前、后车身结构模态频率对比如表3所列,门窗框对角线变形量对比如表4所列。
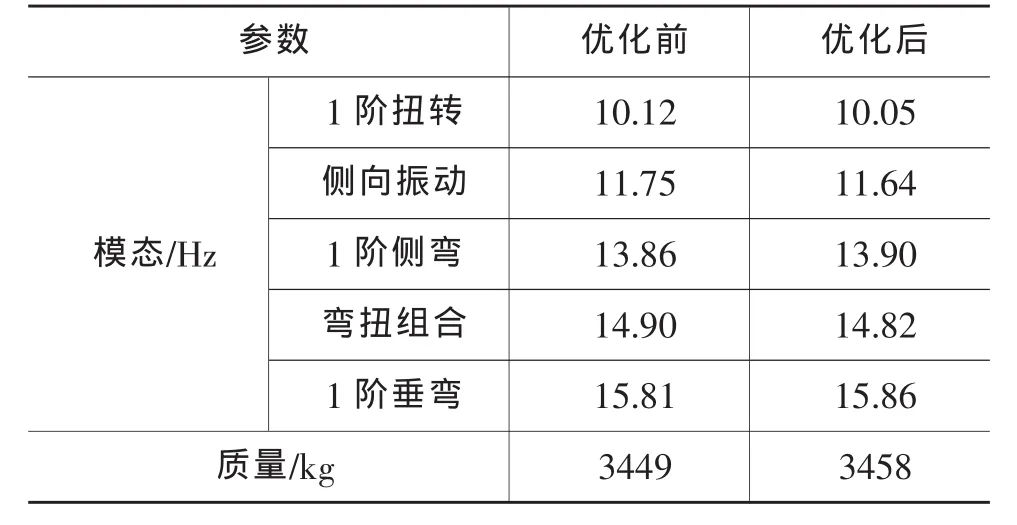
表3 优化前、后车身结构模态对比
由表3可知,在车身骨架质量略有增加的情况下,车身骨架结构的固有振动特性基本保持不变。
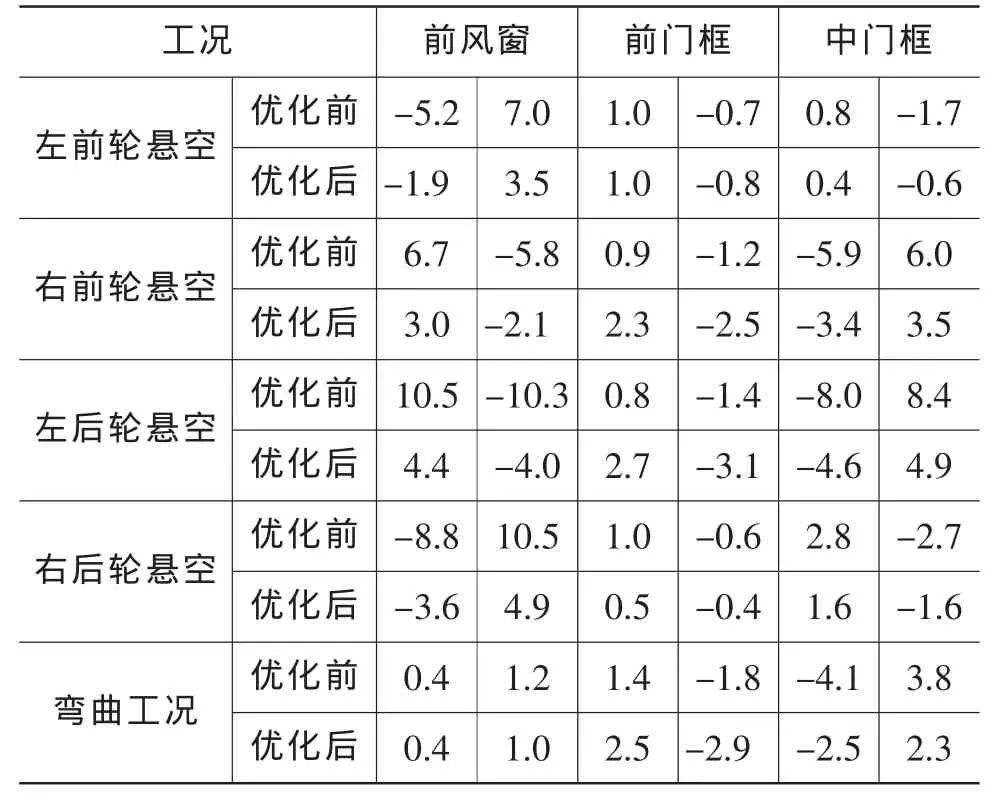
表4 优化前、后门窗框对角线变形量对比 mm
由表4可知,优化后各静态工况下门窗框的对角线变形量都在5 mm以内,较优化前下降了很多,满足了对门窗框对角线变形量的要求,优化后车身开口处刚度明显提高,优化效果显著。
此外,车身试验扭转刚度由优化前的39 614.1 N·m/(°)提高到 4 1761.0 N·m/(°),增幅 5.42%,说明车身开口刚度和整体刚度有紧密联系。通过优化门窗变形量可以有效提高车身结构的扭转刚度,对于客车车身结构的设计和优化具有指导意义。
5 结束语
本文建立了某大型客车车身骨架有限元模型并进行了模态和静态刚度分析,在此基础上进行门窗口变形优化,得到如下结论:
a. 通过灵敏度分析,引入相对灵敏度指标,据此筛选出优化过程的设计变量用于门窗框对角线变形量的优化,以较少的结构修改实现大型客车门窗口刚度优化,方法合理高效。
b. 由优化结果可知,通过优化门窗口变形,提高门窗开口刚度,使得车身结构的扭转刚度明显提高,可见门窗开口刚度与车身结构扭转刚度有密切联系。
1 刘惟信.汽车设计.北京:清华大学出版社,2001.
2 高云凯,王婧人,汪翼.基于正交试验的大型客车车身结构多工况拓扑优化研究.汽车技术,2011,11:16~19.
3 陈光,崔玲,高云凯.大客车车身结构多工况综合优化分析.山东大学学报,2009,12:88~92.
4 Yu Cheng Lin, Hong CHiNian.StructuralDesign Optimization of the Body Section Using the Finite Element Method.SAE 2006-01-0954.
5 Y.K Gao,P.Liu.Optimization Analysis for Fuel Cell Body Structure in Multi-load Case.Advanced Material Research Vols.44~46(2008):401~408.
6 高云凯.汽车车身结构分析.北京:北京理工大学出版社,2006.
7 高云凯,杨欣,金哲峰.轿车车身刚度优化方法研究.同济大学学报,2005,33(8).
8 丁炜琦,苏瑞意,桂良进,范子杰.基于应力优化的大型客车结构多目标优化.汽车技术,2010,4:4~7.
9 Hailiang Wang, Xianlong Jin, Zhongqin Lin.FEM Static and Dynamic Analysis of the Body Structure of SK6120 Low Floor City Bus.SAE 2002-01-0813.

