半模机翼振动对气动性能影响的风洞试验研究

解亚军，叶正寅

（西北工业大学翼型、叶栅空气动力学国防科技重点实验室，西安 710072）

0 引 言

风洞试验是研究飞行器气动性能的主要手段之一，影响飞行器模型试验精度的因素多种多样且相互关联。目前，除了已经研究较多的风洞流场、天平性能、模型定位、角度精确测量与控制等因素外，模型－支架系统的振动对试验结果会带来严重影响［1］，尤其对大展弦比飞机模型，如大型运输机和高空长航时无人机等飞行器，这种影响表现得更为突出［2－4，6］。结合国家自然科学基金项目和985建设项目，研制了专门的半模机翼振动模型，为了研究不同机翼的性能，将机翼设计为可更换的。目前设计的两种机翼翼型分别为NACA0012和NACA64－210。选取5种激振方式，通过直接测力法得到了模型在静态和不同激振方式下纵向气动特性变化曲线，分别研究了雷诺数、自然转捩和固定转捩、数据采集方式等参数对机翼气动特性的影响。试验结果表明：振动对机翼纵向气动特性的影响因不同翼型构型、不同采集方式和翼面不同流动模式等会产生不同效果，并对三元半模测力试验与二元测压试验和数值模拟计算结果之间存在差异的原因进行了初步分析和探讨。

1 试验方法

试验是在西北工业大学翼型研究中心某低速风洞的三元试验段中进行的。通过模型机翼翼梢5种不同偏心块来改变模型的振动频率和振幅，以机翼弦长为特征值的试验雷诺数Re＝0.342×106。采用升华法观测机翼表面静态与动态边界层转捩或分离位置变化。将半翼展机翼模型固定在盒式天平浮动框连接板上，模型机身与机翼和天平之间保持间隙，不可传力。模型机身处考虑风洞边界层厚度［8］。天平安装在与洞壁固定的支座上，见图1。当机翼翼梢电机带动5种不同的质量块旋转时，机翼产生某一频率的振动，仅以频率表示，这项工作需在模型进洞前测试，两种半模测试结果见表1和2。根据常规半模试验方法和坐标转换，得到模型在静、动态下的气动力。采用通用接头可以实现两种机翼的互换。试验迎角由风洞转盘门实现。

表1 NACA0012翼型机翼模型振动参数（电机功率25W）Table 1 The vibration parameters of the model wing with NACA0012airfoil（power：25W）

表2 NACA64－210翼型机翼模型振动参数（电机功率20W）Table 2 The vibration parameters of the model wing with NACA64－210airfoil（power：20W）

图1 模型安装在NF－3风洞中Fig.1 The test model installed in wind tunnel

2 试验模型及设备

2.1 试验模型

试验模型机身为钢芯木制结构，机翼采用弹性模型设计。半模机身长1800mm，最大横截面圆半径109.5mm，并考虑风洞边界层厚度100mm。机翼展长1250mm，弦长250mm。激振电机安装在机翼翼梢型面内，偏心杆和偏心块在整流包内转动，防止偏心机构对来流干扰。为了防止电机运转过程中过热烧坏，在电机附近的机翼和整流包上加工了许多小孔（见图2），以便电机散热。

图2 模型顶部散热孔Fig.2 The holes on the top of the model for hot reduction

在试验前用LMS SCADAS III应力应变测量仪获得实物模型的固有力学特性。NACA0012机翼的一阶模态为弯曲变形，固有频率5.27Hz，二阶模态为扭转变形，固有频率29.16Hz；NACA64－210机翼的一阶模态和二阶模态与前者相同，其固有频率分别为4.47Hz和22.15Hz。

2.2 风洞

试验是在NF－3风洞三元试验段中进行的。NF－3风洞是一座低速直流式风洞，共有3个可更换使用的试验段。除三元试验段外，还有二元试验段和螺旋桨试验段，可分别进行翼型研究和螺旋桨性能测试研究。三元试验段为切角矩形截面，高为2.5m，宽为3.5m，长12.0m。空风洞最大风速可达90m／s，最小稳定风速为10m／s，湍流度为0.078%，轴向静压梯度dCp／dx＝0.0066（1／m）。

2.3 数据采集系统

测力数据采集系统采用中国成都华太公司开发生产的VXI测量系统的稳态测量部分和动态测量部分，见图3。稳态数据采集模板具有64通道数，A／D位数16位，采集速度不小于100Hz；配备10Hz固定低通滤波器和放大器，放大倍数满足微伏级和毫伏级信号测试；试验中扫描速度和扫描通道顺序可根据试验要求单独设定，在试验时可根据实际情况选择。

动态数据采集系统有32个通道，16位A／D转换，采集速度每通道100kHz。试验稳态采集频率200Hz，滤波频率3Hz；动态数据采集频率500Hz，滤波频率100Hz，每个迎角状态采集时间20s。

2.4 试验天平

试验使用一台六分量盒式应变天平。天平的量程和校准精度及准度见表3。

图3 VXI数据采集系统Fig.3 The VXI data acquisition system

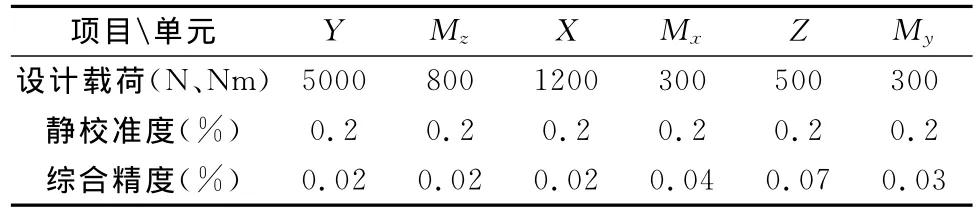
表3 盒式天平技术参数Table 3 Parameters of the box－balance

2.5 偏心块

偏心块用来产生模型的激振力，偏心轴中心位于翼型弦线上，距前缘125mm，距机翼根部1080mm。5种偏心块的外形见图4，编号从下至上依次为1＃～5＃，用于NACA0012机翼的为11＃～15＃，用于NACA64－210机翼的为21＃～22＃。

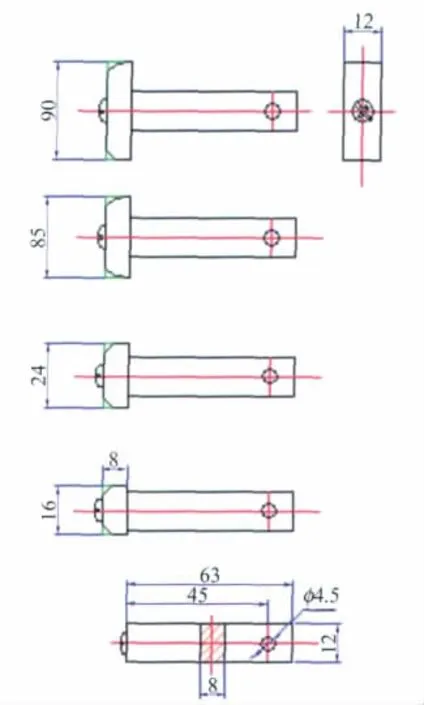
图4 偏心块外形Fig.4 Five sketches of the bias rods for vibrating

3 数据处理

静态试验数据和动态试验稳态采集的数据均由VXI系统按常规模型试验方式经过天平公式进行预处理，得到天平校心处的模型气动力，按公式（1）转换成力（或力矩）系数。动态试验动态采集数据则由VXI系统按天平输出的8个通道得到随时间变化的动态电压信号，将采集时间段内的电压值取平均后，代入天平公式求得气动力值，与静态试验同样的方法得到升力系数。

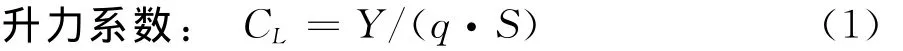
公式中q为试验动压，单位Pa；Y为天平测量的升力，单位N；S为参考面积。

4 试验结果与分析

4.1 模型静态与动态试验结果

图5和6给出了NACA0012对称翼型的半模机翼在雷诺数一定条件下，分别用稳态数据采集模式和动态数据采集模式时自然转捩和固定转捩下的升力特性曲线。为了说明方便起见，图标“f＝0”表示静态试验状态，其余表示不同偏心块产生的频率，并将NACA0012对称翼型的半模机翼标记为“Ⅰ号”，将NACA64－210层流翼型的半模机翼标记为“Ⅱ号”。从中可以看出，在自然转捩条件下，模型振动时的最大升力系数和失速迎角比静态时有增大趋势，而且升力在失速迎角以后的下降趋势比较平缓，说明振动对失速特性有所改善；而在固定转捩条件下，模型振动时的最大升力系数与静态时基本一致，说明在湍流流动条件下振动和数据采集方式对该模型机翼的升力特性无明显影响。图7是NACA64－210层流翼型的半模机翼在相同雷诺数时自然转捩的升力特性曲线，其变化规律与NACA0012固定转捩情况类似。

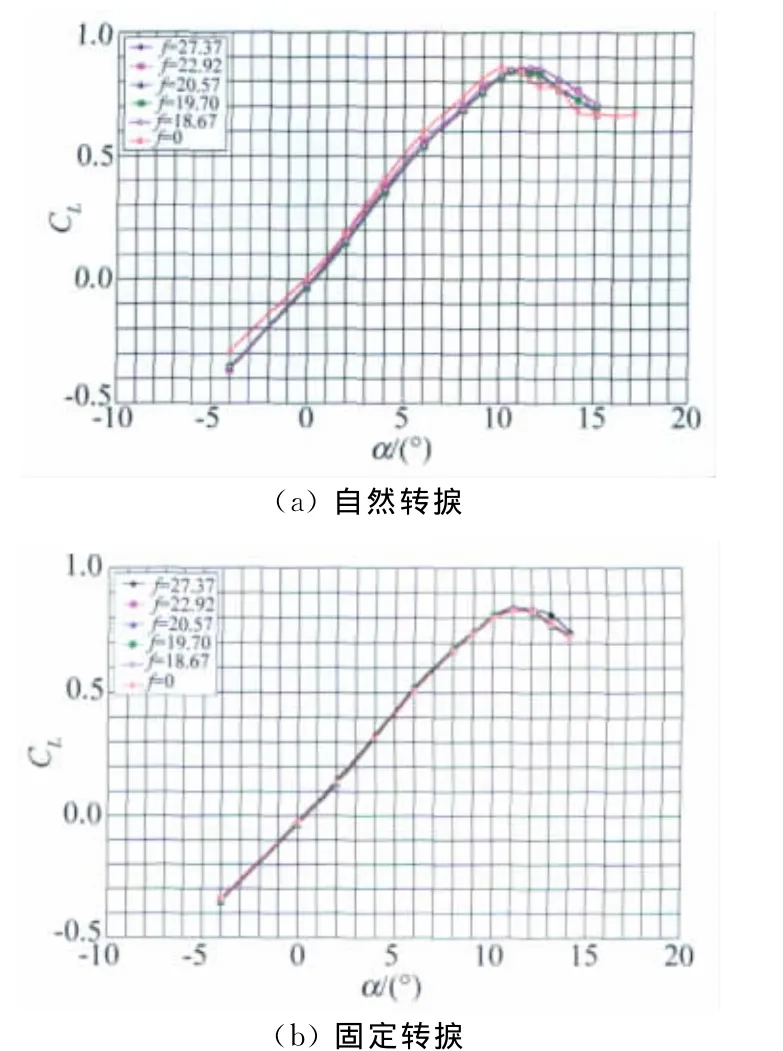
图5 Ⅰ号模型机翼稳态采集时有无振动的升力曲线（Re＝0.342×106）Fig.5 The lift performance of theⅠ＃half－model wing with or without vibration under static acquisition（Re＝0.342×106）

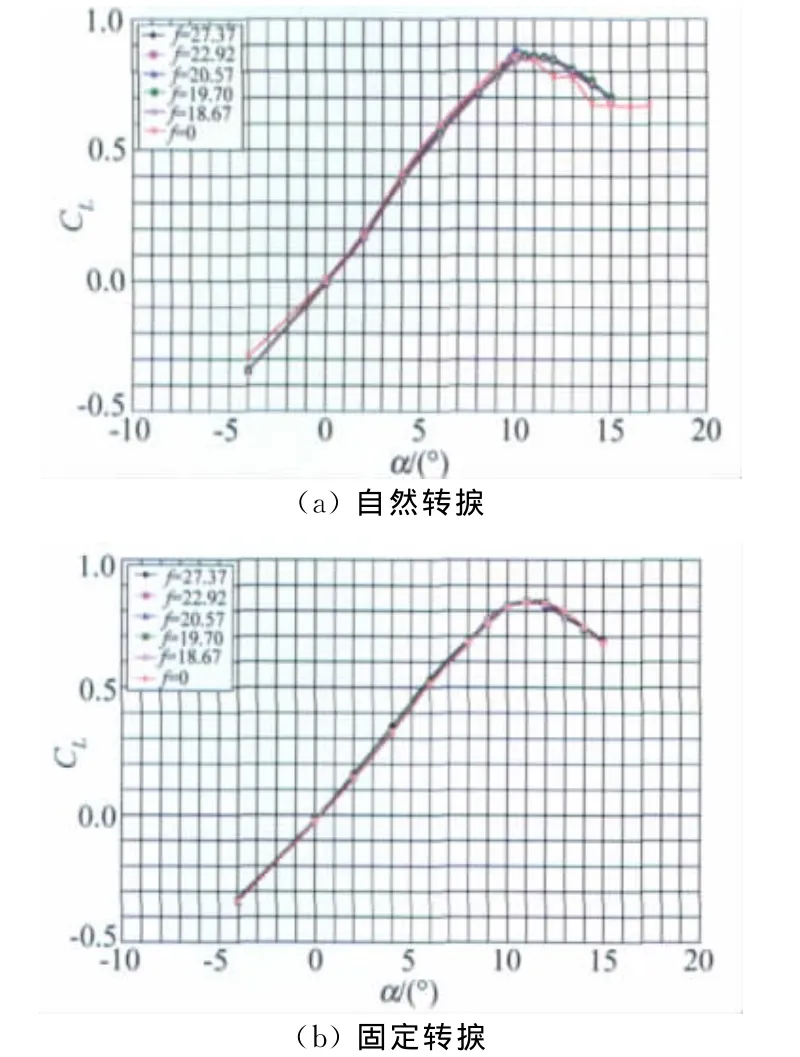
图6 Ⅰ号模型机翼动态采集时有无振动的升力曲线（Re＝0.342×106）Fig.6 The lift performance of theⅠ＃half－model wing with or without vibration under dynamic acquisition（Re＝0.342×106）

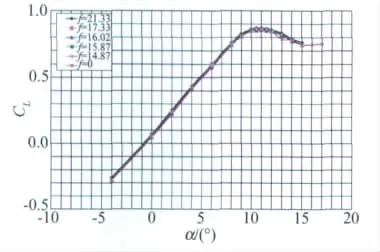
图7 Ⅱ号模型机翼稳态采集时有无振动的升力曲线（Re＝0.342×106）Fig.7 The lift performance of theⅡ＃half－model wing with or without vibration under static acquisition（Re＝0.342×106）

4.2 与翼型测压试验和文献的比较

文献［7］给出的二元翼型振动试验结果和文献［4，6］给出的计算结果均表明，振动会造成翼型大迎角下升力系数的减小和失速的提前，而半模机翼振动测力试验中的情况与之不一致。分析其原因，首先两次试验的折算频率不同，翼型振动试验受机构条件限制，最高频率仅为1Hz，折算频率k＝0.19（k＝2πfb／v，b为弦长，v为来流速度），半模实验最大折算频率k＝1.432；其次半模试验中的激振方式不是单纯施加沉浮或俯仰运动；此外半模机翼本身的惯性力影响无法扣除；以上原因还需要经过大量的试验和计算进行深入研究。

5 结 论

综合试验结果对比和数值模拟的初步分析，可以看出，模型机翼振动对气动力影响的因素多且复杂，模型振动对机翼纵向气动特性的影响因不同翼型构型、不同采集方式和翼面不同流动模式等会产生不同效果，如模型振动可以改善NACA0012翼型机翼的失速性能；在自然转捩失速前，振动使机翼升力有所减小；振动对对称翼型和层流翼型机翼影响情况不同等。对于半模测力试验结论与前期的二元翼型振动试验和计算结果不一致的原因还有待于作进一步研究。

该期对NACA0012模型、11＃偏心块、自然转捩振动、稳态采集模式的试验状态进行7次重复性试验，升力系数的均方根误差σCL＝0.0018，小于国军标合格指标的0.004，表明该期试验数据可信。

［1］ 恽起麟.提高风洞实验数据精度的方法［J］.气动实验与测量控制，1994，8（3）：74－81.

［2］ WHITING R J，DELAMORE－SUTCLIFFE D W，GREENWELL D.Experimental and numerical study of gust loads on stall flutter initiatio［R］.AIAA Paper 2005－5097.

［3］ YE Zhengyin，XIE Fei.The effects of elastic vibrations on the flow field near stall－incidence of the airfoil［C］.Proceedings of the Sino－Russian Conference on Aerospace Technology，April 16－17，2006，Xi＇an，China，348－353.

［4］ 叶正寅，谢飞.不同振动形式下的翼型失速特性［J］.空气动力学学报，2008，26（1）：0258－1825.

［5］ 陈桂彬，邹丛青.气动弹性设计基础［M］.北京：北京航空航天大学出版社，2004.

［6］ 宋保方.大功角下振动对机翼气动特性影响的计算研究［D］.西北工业大学硕士学位论文，2010.

［7］ 解亚军，叶正寅.翼型大迎角振动对气动性能影响的实验研究与初步分析［J］.实验流体力学，2010，24（4）：25－28.

［8］ 恽起麟.风洞试验［M］.北京：国防工业出版社，2000.