小波熵和BP神经网络在孤岛检测与扰动辨识中的应用

梁雪飞，陈歆技

(东南大学电气工程学院，江苏南京210096)

伴随着全球范围内的能源危机，新能源技术受到了世界各国更多的关注。风力发电、光伏发电等分布式电源（DG）接入系统可能引起的孤岛现象受到人们越来越多的重视，孤岛检测成为光伏系统并网所必须解决的一个技术问题[1，2]。传统的孤岛检测技术主要检测电压与频率的波动；与被动检测法相比，主动检测法可以在降低检测盲区的同时，有效地判别孤岛的发生，但其向系统中注入的扰动变量对电能质量的影响不可忽视[3]；同时，电力系统中可能存在电压或频率波动、谐波或噪声等污染，这些因素给孤岛现象的检测带来了一定的困难[4-8]，因此，如何有效区分系统扰动与孤岛现象的发生成为孤岛检测检测技术的关键。

小波熵[9，10]以其出色的信号分析与处理能力广泛地应用于电力系统的故障检测与诊断中。神经网络[11，12]作为人工智能算法，其实质反映了输入转化为输出的一种数学表达式，能够通过对输入样本的训练，提取信号的特征，进而对输入的检测信号进行有效分类与辨识。以公共耦合点的电压作为采样信号，借助BP神经网络，通过小波熵值的变化对孤岛的发生进行有效检测，理论与仿真验证表明，该算法能够准确识别孤岛发生与电压扰动，从而避免光伏逆变器的误动作。

1 基于多分辨率分析的小波变换与小波熵

1.1 基于多分辨率分析的小波分解与重构

（1）对长度为N的离散信号采用Mallat算法[13]进行处理，将上一级信号通过高通滤波器Hi_D与低通滤波器Lo_D后，分别得到原信号的细节分量与近似分量，如式（1）所示；随后对信号的近似分量继续分解，再次通过高通、低通滤波器，这样，在选择了合适的小波基函数与分解层数的基础上，原信号经过尺度j=1，2，3，…，J（其中J为最大分解尺度）的分解，最终得到D1，D2，D3，…，AJ，其中，D1，D2，D3，…，DJ-1与AJ分别表示信号的高频细节分量与低频近似分量。

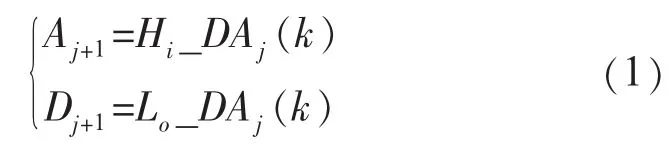
（2）对分解后的各层系数进行小波变换系数的重构，重构高通、低通滤波器系数分别为与其中与分别是与的对偶算子。

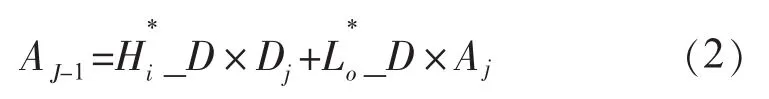
上述即是基于多分辨率分析的小波分解与重构算法。

1.2 小波熵

熵是表征信息的一个普适量[9]，Shannon的信息熵理论指出，对于一个不确定的系统，若用一个取有限值的随机变量表示其状态特征，取值为xi的概率pi为：

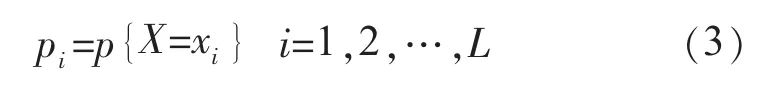
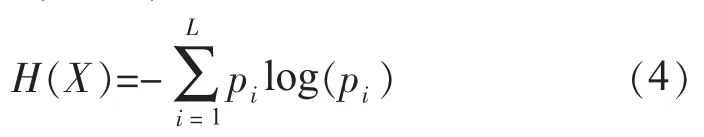
其中，当pi=0时，pilog（pi）=0，信息熵H是在一定的状态下定位系统的一种信息测度，是对序列未知程度的一种度量，可以用来估计随机信号的复杂性。

1.3 小波熵的构造

就多尺度小波分解而言，在某一时间窗内，信号的总能量Ppower等于各分量能量之和，进而设因而有于是可定义小波熵WEE为[9]：

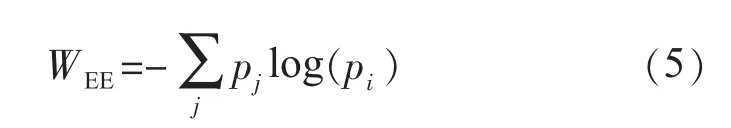
2 BP神经网络

BP神经网络，即误差反向传播算法的学习过程，由信息的正向传播和误差的反向传播2个过程组成。BP神经网络的出现成功解决了求解非线性连续函数多层前馈神经网络权重调整问题，广泛应用于函数逼近、模式识别/分类等领域。

BP神经网络的节点输出模型如式（6）和式（7）所示。隐层节点输出模型为：

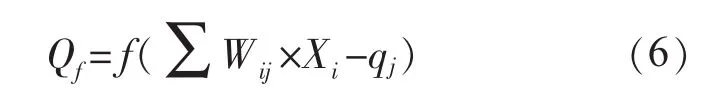
输出层节点输出模型为：

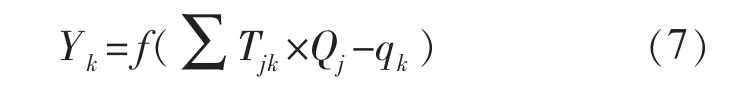
式中：f为非线性作用函数；q为神经单元阈值。典型BP网络结构模型如图1所示。

3 基于小波熵与BP神经网络的孤岛检测与扰动辨识

考虑到孤岛现象的发生往往伴随着电压幅值或频率的变化，因此基于小波熵与BP神经网络的孤岛检测技术的基本原理是根据光伏电源与本地负载的公共耦合点的采样电压在故障前后的变化来判别当前运行状态。将公共耦合点的采样电压经小波分解与系数重构后，计算其各层系数的小波熵值[14，15]，并以此作为BP神经网络的输入值，经神经网络系统处理判别后确定当前电力系统所处的运行状态，进而控制相应的保护装置是否将光伏系统切除。

文中采样电压信号选自光伏系统与本地负载连接的公共耦合点处，为保证采样信号的准确性，采样频率为6400Hz，即每周波1280 点的采样速率，经小波变换系数分解与重构后，并根据式（5），分别计算其各层系数的小波熵，此后，将计算出的小波熵值作为神经网络的输入，用于判断当前系统所处运行状态。文中选择db6小波对采样信号进行小波分解与重构；神经网络采用三层BP网络，训练函数选择tansig函数。根据设计的需要，输入层为6个输入单元，输出层1个输出单元，而隐层节点个数根据经验公式（8）[16]选择为12个。

式中：n为隐层节点个数；ni为输入节点数；no为输出节点数；a为1～10之间的任意常数。

文中主要目的在于将电网电压扰动与孤岛现象的出现进行有效辨识，以避免光伏并网逆变器的误动作。由于要区分的只是两类情况，而BP神经网络的输出值可以限定在（-1，1）范围内，这样通过给定相应的训练数据使得yi=-1表示电网电压扰动（非孤岛），yi=1表示孤岛发生。

4 仿真实验与数据分析

4.1 光伏模型及仿真实验

通过Matlab/Simulink对4kW单向光伏并网系统进行建模仿真，电网电压的有效值为220V，负载品质因数以Qf=2.5为例，谐振频率为50 Hz，如图2所示。

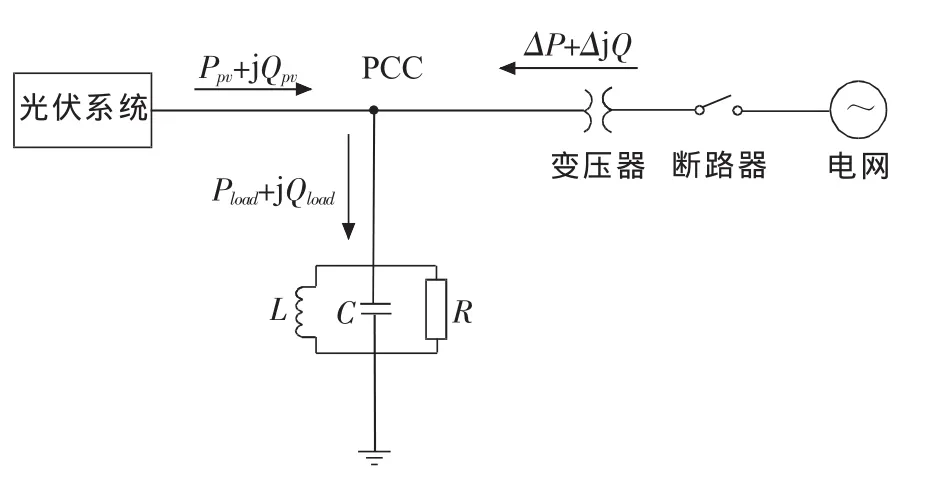
图2 单向光伏并网系统

仿真中以断路器在0.08s断开模拟孤岛现象的发生；为电网电压施加的扰动时间为0.08～0.14s，持续3个周期共0.06s。

以公共耦合点的电压作为采样信号，每周波128个采样点，采样频率为6400Hz，仿真时间为0.2s，共1280 个采样点。对采样信号采用db6小波进行6层分解。针对两类情况4种信号（电压暂升与暂降、孤岛压降与压升），分别选取40个样本作为BP神经网络的训练数据，然后选取60个样本进行测试。

4.2 数据分析

4.2.1 采样信号的小波熵值

对孤岛后电压升高与降低、电网扰动所致的电压暂升与暂降4种信号进行小波分解与系数重构，分别选取40组数据作为BP神经网络训练数据输入。4种情况下部分小波熵值如表1所示（以电压暂升和暂降10%，孤岛后电压升高和降低10%为例）。

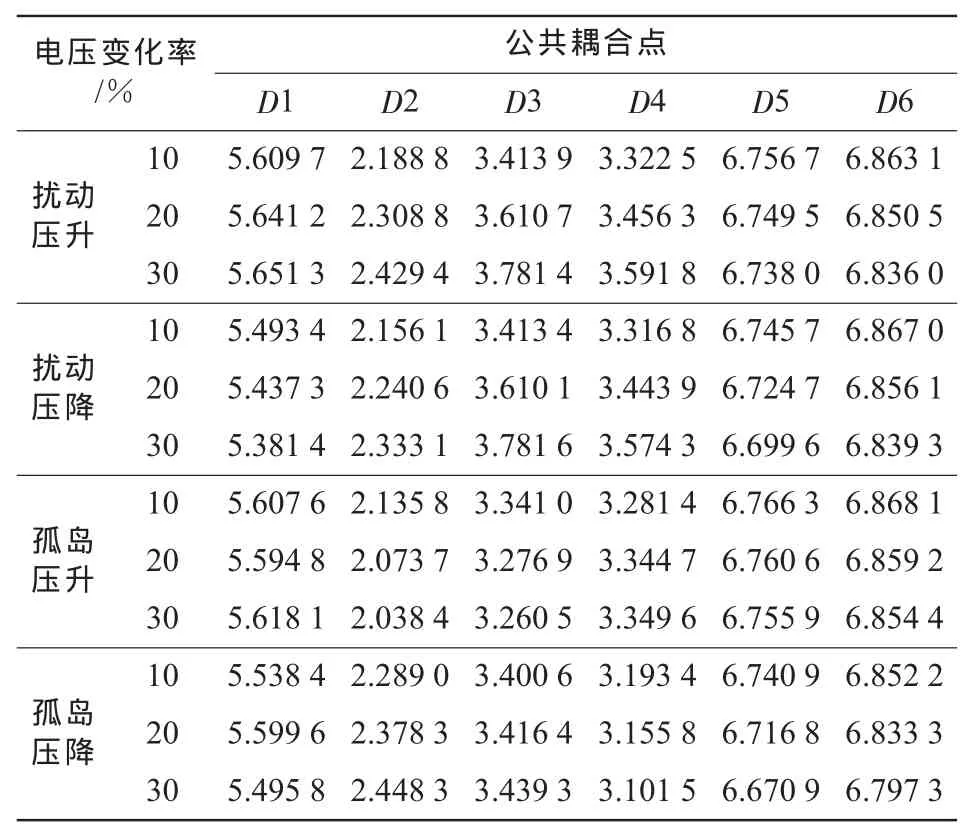
表1 两类信号的小波熵值表

对表1中的小波熵值进行分析，可以看出：同类样本（孤岛后电压升高与降低、电网扰动所致电压暂升与暂降）之间小波熵值的变化趋势非常相似；不同类样本（孤岛与非孤岛）之间，小波熵值存在一定不同，但差异不大。由此需要借助BP神经网络来辨识2类情况下小波熵值的内在特征，从而有效实现区分孤岛与非孤岛状态的目的。

4.2.2 算例测试

针对训练好的BP神经网络，选取2类信号共60组数据作为测试数据来验证所提出算法的准确性。测试结果如表2所示（选取其中的12组列表）。

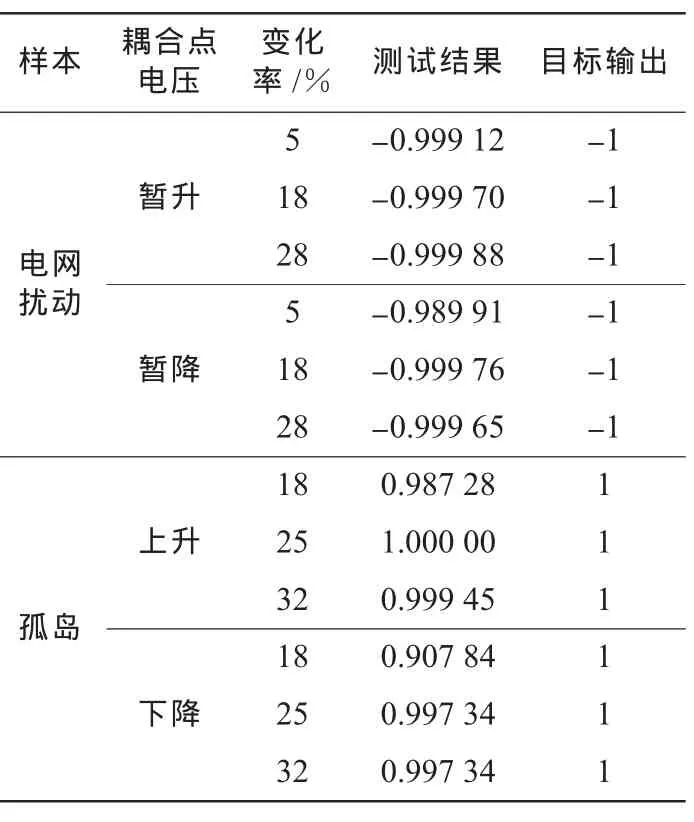
表2 BP神经网络测试结果

表2中BP神经网络的测试结果与目标输出误差相对较小，可以准确有效地将孤岛与扰动区分。

4.2.3 噪声测试

电力系统测试中不可避免的会受到噪声的影响，因此在进行孤岛与扰动区分时必须将噪声污染加以考虑。在采样信号中加入信噪比为20 dB的高斯白噪声，选取30组测试数据再次进行孤岛与扰动的辨识。受篇幅限制，表3只列出其中的8组数据。

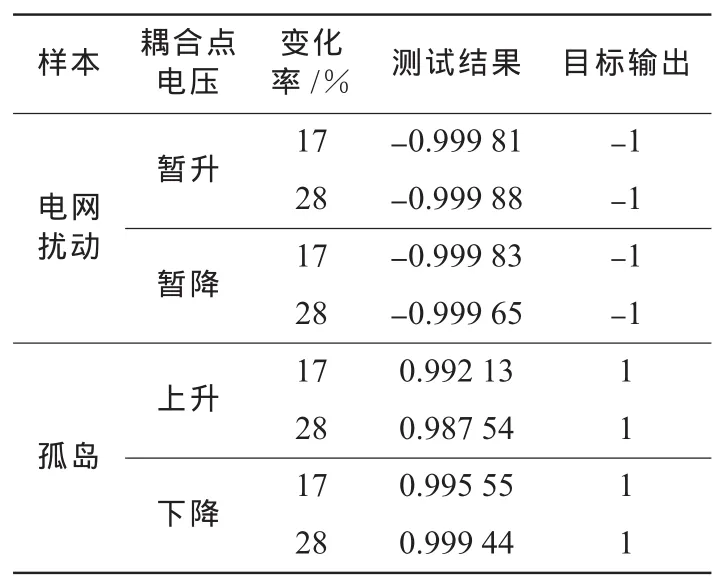
表3 BP神经网络噪声测试结果

添加噪声后，各组信号的各层熵值发生明显变化，但仍然保持表1所描述的特性，并没有影响最终的测试结果。因此该算法具有较高的准确性。

5 结束语

文中将小波熵与BP神经网络结合起来，作为光伏并网系统的一种孤岛检测技术。选取公共耦合点的电压作为参考输入，进行小波变换与系数重构后，计算每一层系数的小波熵，以此作为BP神经网络的训练输入。仿真算例表明，该设计方案能够有效地区分孤岛与扰动，进而避免光伏并网逆变器的误动作。

[1] IEEE Std 929－2000，IEEE Recommended Practice for Utility Interface of Photovoltaic(PV）Systems[S].

[2] 曹海燕，田悦欣.并网逆变器孤岛控制技术[J].电力系统保护与控制，2010，38（9）：72-74.

[3] 郭小强，赵清林，邬伟扬.光伏并网发电系统孤岛检测技术[J].电工技术，2007，22（4）：157-162.

[4] 禹华军，潘俊民.无功补偿技术在光伏并网发电系统孤岛检测中的应用[J].电工电能新技术，2005，24（3）：22-26.

[5] 刘芙蓉，康勇，段善旭，等.主动移频式孤岛检测方法的参数优化[J].中国电机工程学报，2008，28(1)：95-99.

[6] 李军，黄学良，陈小虎，等.基于分压器原理的孤岛检测技术在微电网中的应用[J].中国电机工程学报，2010，30（34）：15-21.

[7] 李春玲.基于光伏并网发电系统的孤岛检测[D].天津：天津大学，2008.

[8] PIGAZO A，LISERRE M，MASTROMAURO R A，et al.Wavelet-based Islanding Detection in Grid-connected PV Systems[J].IEEE Transactions on Industrial Electronics，2009，56(11)：4445-4455.

[9] 何正友，刘志刚，钱清泉.小波熵理论及其在电力系统中应用的可行性探讨[J].电网技术，2004，28（21）：17-21.

[10] 刘瑞叶，龙志刚.小波熵及小波变换的短期负荷预报[J].哈尔滨理工大学学报，2007，12(4)：62-65.

[11] 丛爽.面向Matlab工具箱的神经网络理论与应用[M].合肥：中国科学技术大学出版社，2009.

[12] 侯媛彬，杜京义，汪梅.神经网络[M].陕西：西安电子科技大学出版社，2007.

[13] 郭晶，孙伟娟.小波分析理论与matlab7实现[M].北京：电子工业出版社，2005.

[14] 朱艳伟，石新春，李鹏.分辨奇异谱熵和支持向量机在孤岛与扰动识别中的应用[J].中国电机工程学报，2011，31(7)：64-70.

[15] 何正友，钱清泉.多分辨信息熵的计算及在故障检测中的应用[J].电力自动化设备，2001，21(5)：9-11.

[16] 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2009.