火炬塔架抗剪键设计方法探讨

王冰仓

(洛阳石油化工工程公司土建室，河南 洛阳 471003)

火炬塔架属空间桁架结构，因其高度常常达100多米，质量又很轻，风荷载常成为控制设计的荷载。因柱底常出现拔力不能考虑底板与混凝土之间的摩擦力，而《钢结构设计规范》又规定柱脚锚栓不宜用于承受剪力，因此需要设置抗剪键。抗剪键的设计，在现行各种结构设计规范中并没有具体的计算方法，现结合工程实践探讨抗剪键设计的方法。

设计资料:该塔架高114 m，采用四边形平面布置，地面层边长20 m。在沿对角线风荷载的作用下，图1中84号支座的水平反力最大。

最不利内力如下:

垂直力:Fy=－2927 kN。

水平力:Fx=535 kN，Fz=535 kN。

钢材强度等级:Q235，fy=235 N/mm2，fv=125 N/mm2。

混凝土强度等级:C30，fc=14.3 N/mm2。

1 抗剪键截面按轧制H型钢HW400×400设计

截面尺寸:

翼缘:bf=400 mm，tf=21 mm。

腹板:h=400 mm，tw=13 mm，hw=400－30=370 mm。截面示意图见图2。

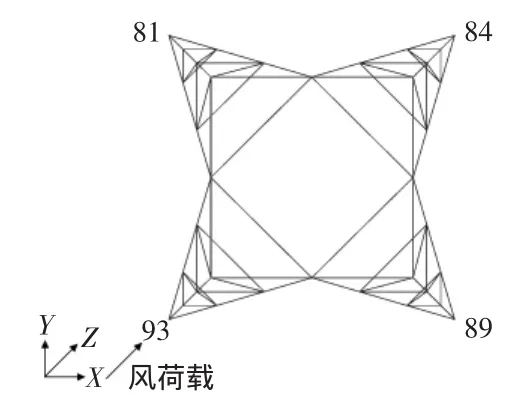
图1 塔架在风荷载作用下的水平反力

图2 截面示意图

抗剪键长度:取L=400 mm＜1.5h=600 mm。

截面特性:

1)中性轴以上截面，z轴左半部分截面分别对x及z轴的面积矩:

Sx=(0.5hw× tw)× 0.25hw+bf× tf× (0.5hw+0.5tf)，Sx=1800 mm3;

Sz=4 × (0.5bf× tf)×0.25bf，Sz=840 mm3。

2)整个截面绕x及z轴的惯性矩:

Ix=2bf× tf× (0.5hw+0.5tf)2+twh3w/12=20500 mm4，Ix=65000 mm4;

Iz=(2tf×b3f+hwt3w)/12，Iz=22000 mm4。

3)角点a处的截面抵抗矩:

Wx=Ix/0.5h，Wx=3300 mm3;

Wz=Iz/0.5bf，Wz=1100 mm3。

2 抗剪键强度计算

2.1 抗剪键受力分析

抗剪键通过与底板的连接焊缝将柱脚水平力传至基础，水平力作用下抗剪键受力类似于悬臂梁，假定混凝土压应力沿抗剪键长度方向为三角形分布。

计算截面作用计算:

剪力:Vx=Fx=535，Vz=Fz=535。

弯矩:Mx=Vz×L/3=71.2，Mz=Vx×L/3=71.2(见图3 ～图5)。

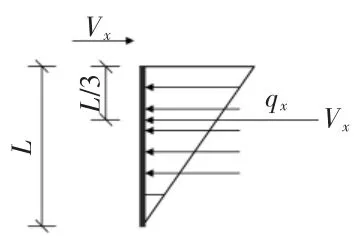
图3 压应力分布图

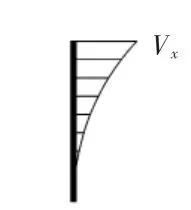
图4 剪力

图5 弯矩

2.2 抗剪强度计算

应力计算位置:

b点:τb=Vz×Sx/(Ix×tw)=113.4 N/mm2＜fv=125 N/mm2。

c点:τc=1.5 ×Vx/(2bf×tf)=47.8 N/mm2＜ fv=125 N/mm2。

2.3 抗弯强度计算

a点:σa=Mx/wx+Mx/wz=127.3 N/mm2＜ fy=215 N/mm2。应力计算位置见图6。

2.4 折算应力计算

轧制型钢梁，不必验算。

3 抗剪键与柱脚底板的连接焊缝计算

采用直角角焊缝，沿H型钢周围围焊。焊缝连接计算简图见图7。

图6 应力计算位置

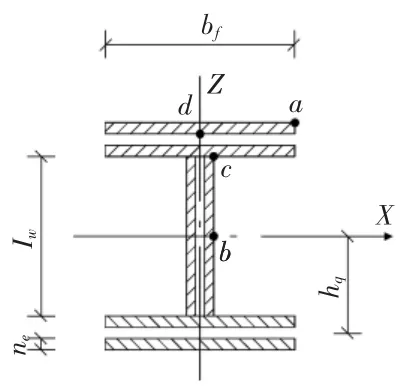
图7 焊缝连接计算简图

角焊缝强度设计值:ffw=160 N/mm2。

焊缝厚度:hf=12，he=0.7hf=8.4 mm。

翼缘焊缝形心至 x轴距离:hq=0.5h －0.5tf=189.5 mm。整个截面绕x轴，z轴惯性矩:

Ix=(4×bf×he)×h2q+2he×l2w=53000 cm4，Iz=4×he×b3f/12=18000 cm4。

截面抵抗矩:

a 点:Wxa=Ix/(0.5h+he)=2600 cm3。

c点:Wxc=Ix/(0.5h－he)=3000 cm3。

d 点:Wxd=Ix/0.5h=2700 cm3。

b点以上截面对 x轴面积矩:Sxb=2bf×he×hq+lw×he×0.25lw=1500 cm3。

翼缘部分截面对x轴面积矩:Sxc=2bf×he×hq=1273 cm3。

各应力计算点的计算及验算公式见表1。

表1 各应力计算点的计算及验算公式

3.1 a点

σa=Mx/Wxa+Mz/Wza=106.7 N/mm2＜ffw=160 N/mm2。

3.2 b点

τb=Vz× Sxb/(Ix×2he)=89.8 N/mm2＜ ffw=160 N/mm2。

3.3 c点

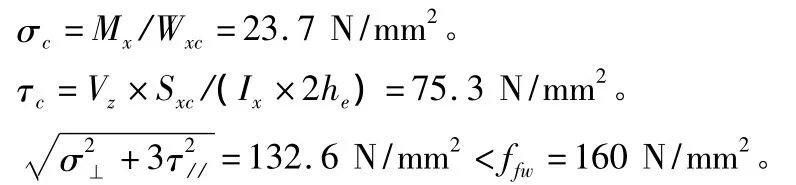
3.4 d点

4 按箱形截面计算

应力计算简图见图8。

4.1 截面尺寸

b1=300 mm，δ1=20 mm，长度 L=300 mm。

4.2 截面特性

Ix=Iz=［b41－ (b1－2δ)4］/12=29000 cm4。

Wx=Ix/(0.5b1)=2000 cm3，Wz=Iz/(0.5b1)=2000 cm3。

Sx=Sz=0.5［b21－ (b1－2δ)2］×0.25b1=840 cm3。

4.3 强度计算

最大剪应力:τb=τc=1.5Vz/(2b1×δ1－δ21)=69.2 N/mm2＜fv=125 N/mm2。最大正应力:σa=Mx/Wx+Mz/Wz=54.5 N/mm2＜fy=215 N/mm2。

4.4 焊缝连接计算

焊缝计算截面见图9。

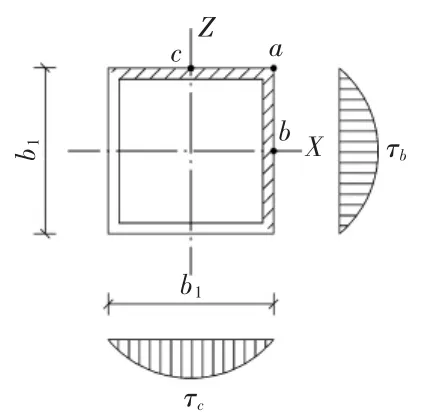
图8 应力计算简图

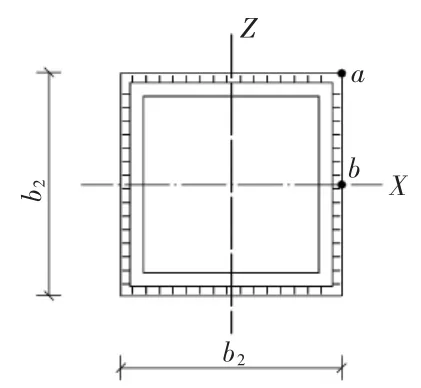
图9 焊缝连接计算截面

采用直角角焊缝:hf=15 mm，he=0.7hf=10.5 mm。

焊缝截面尺寸:b2=b1+2he=321 mm，δ2=10.5 mm。

最大剪应力:τb=121.0 N/mm2＜ffw=160 N/mm2。

最大正应力:σa=Mx/Wx+Mz/Wz=81.9 N/mm2＜ffw=160 N/mm2。

4.5 混凝土抗压强度的计算

混凝土局部抗压承载力:

Vu=0.9βcβlfcAn(参考《混凝土结构设计规范》7.8.3-1 式)。

抗剪键侧面受压面积:Ax=Ay=b1×L=300×300=90000 mm2。

混凝土抗压承载力:Vux=Vuy=0.9×1.0×1.0×14.3×90000=1158.3 kN。两个方向抗压承载力均大于相应的剪力，故混凝土抗压强度满足要求。

5 结果比较

两种截面形式比较见表2。

表2 两种截面形式比较表

由表2可知，两种截面的截面面积相差仅1.8%，而最大正应力相差达57%，最大剪应力也相差达39%。显然应选择方形钢管作为抗剪键。

6 结语

1)抗剪键决定着柱底剪力能否成功地传给基础，对于重要的建构筑物，应通过计算确定。因其计算涉及到钢结构与混凝土的相互作用，如何在简化计算的情况下又能更好地符合实际情况还需进一步地试验研究。2)对于塔架结构，在沿对角线方向的风荷载控制下，柱底常常存在两个方向数值相当的风荷载，此种情况下应尽可能采用方管，圆管等在各个主轴方向抵抗矩相等或者相近的截面，使截面各部分都充分发挥作用。

［1］GB 50017-2003，钢结构设计规范［S］.

［2］GB 50010-2010，混凝土结构设计规范［S］.

［3］孙训方.材料力学［M］.北京:高等教育出版社，2009.