基于舱室三维重建模型的舱容计量技术研究

胡敏捷阎 利张 毅

（1.上海船舶研究设计院，上海 201203；2.武汉大学，武汉 430079）

0 前言

目前，国内常用的传统舱容计量方法主要有几何测量法以及容量比较法两种［1］。几何测量法通过测量舱室一定高度的特征点拟合出断面的面积，再用断面面积乘以断面间的高度累加得到检定容量。该方法优点是简便快速，但对包含有大曲面构造的复杂舱室，几何测量法的测量密度难以满足计量需求，使得舱容计量精度以及可靠性不高。容量比较法优点是测量准确度较高，容易操作，适用于形状不规则舱室计量，但该方法既耗时又耗水，成本高而效率低，而且难以解决舱室横倾和纵倾状态下的计量问题。

针对传统舱容计量方法的缺点，以近年来发展迅速的地面三维激光扫描测量为技术背景，本文提出了一种基于舱室三维重建模型的舱容计量技术。该方法首先基于舱室三维重建模型对舱室曲面模型进行三角剖分，然后在舱室浮态定义的基础上进行船体剖分三角面片与任意高度水线面的求交计算，最后通过计算三棱锥体积得到当前浮态下的舱容。

从国内外的发展趋势看，液舱容量计量方法已经从接触测量向非接触测量、从手工作业向自动化作业、从事后处理向实时（准实时）处理、从低精度向高精度方向发展。目前在国内外液舱容量计量应用最为广泛的主要为全站仪测量。其特点是单点测量精度较高，但是对于较复杂或存在着大曲面舱壁的舱室而言，全站仪测量明显存在着采样点密度不足、人为影响因素较大、自动化程度不高等技术不足。随着近来地面三维激光扫描测量技术和计算机技术的飞速发展，高效率、高精度以及高密度的点云测量技术突破了传统的单点数据采集模式，能够实现对物体表面完整细致准确的测量，并通过点云数据后处理可以实现对复杂不规则舱室的高精度三维模型重建。这为解决复杂舱室的快速高精度舱容计量提供了新的途径。

本文正是以基于舱室扫描点云数据的舱室三维重建曲面模型为基础，深入研究并提出了一种基于曲面模型三角剖分以及水线面求交的舱容计量新方法。

1 舱室三维模型重建

在获得舱室高密度、高精度的扫描点云数据后，舱室三维模型重建工作可以划分为两大部分。

1.1 舱室表面模型重建

由于舱室表面可以视作为各舱壁光滑曲面拼合而成的封闭模型，因而在舱室表面重建时，可以对各舱壁曲面采用自由曲面重建技术，首先以区域边界构造基面，然后以边界内的点云作为自由曲面型值点求取自由曲面参数［2］，最后通过曲面接边处理完成舱室表面模型重建。

NURBS曲线曲面具有强大的形状定义功能，对复杂的自由曲面有很高的描述精度［3］。在1991年国际标准化组织（ISO）正式发布的工业产品几何定义STEP（Standard for The Exchange of Productmodel data，产品模型数据交换标准）标准中，自由型曲线曲面惟一地用NURBS表示。NURBS特有的几何性质使通用的自由造型技术表达更为容易，也正是因为它的这些性质，使得NURBS曲线曲面在计算机辅助设计和制造中成为标准的设计工具。因而针对舱室表面自由曲面区域的模型重建，本文采用基于区域四边界提取上的NURBS曲面拟合重建技术。图1所示为基于PolyWorks的某舱室表面模型重建结果。

图1 舱室表面模型重建

1.2 舱内构件模型重建及构件管理

舱内构件体积的计量，同样也是舱容积计量的重要部分［4］。舱内构件主要包括输油管、加热管、扶梯以及集油井等内容。在重建过程中，对于管道等结构简单的构件，采取基于点云区域生长的拟合方法进行重建［5］，而对于集油井、扶梯以及支撑架构等复杂构件，则可以采用自定义绘制方法根据构件型材参数进行建模，最后借助于扫描点云通过装配编辑完成舱内构件建模。

由于舱内构件的型材和样式甚多，而且分布不均，为了进行精细的构件扣除计算，提高舱容计量精度及可靠性，所以需要有效地管理这些构件。本文采用文献［6］中基于模型结构树的舱内构件管理方法，结合Access数据库，对舱内重建构件按所属组件、构件名称以及构件型材进行编码并联合构件的几何属性等信息存入数据库。在进行舱容计算的时候，读取数据库中各舱面的构件几何属性数据，根据构件在当前浮态下的垂直分布上下限，计算构件在当前液面高度的被淹没体积，最后通过累加得到当前水线面应扣除的构件体积。舱内管道构件重建示意图如图2所示。

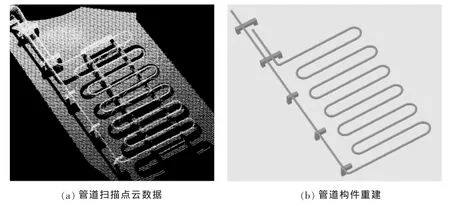
图2 舱内管道构件重建

2 基于舱室三维重建模型的舱容计量

舱体某高度水线面下的体积计算就是由水线面与水线面下舱体曲面所围的复杂封闭区域的体积计算。体积计算从数学原理上均可以表示为解析的三重积分计算，可以运用边界曲面的积分方法，将空间三维封闭区域的几何特性计算转化为沿封闭区域的边界曲面的积分。通过前述的舱室扫描点云数据的模型重建处理操作，舱室模型可以表达为由NURBS表达的自由曲面通过相互连接而形成的表面模型，这使得积分函数与积分域均较复杂，所以无法直接运用公式进行计算，必须采用数值方法，即首先对边界曲面进行三角剖分，然后由曲面上的三个顶点与坐标原点相连构成三棱锥，通过计算大量的三棱锥来计算舱室体积。基于舱室三维模型重建的舱室舱容计量流程如图3所示。

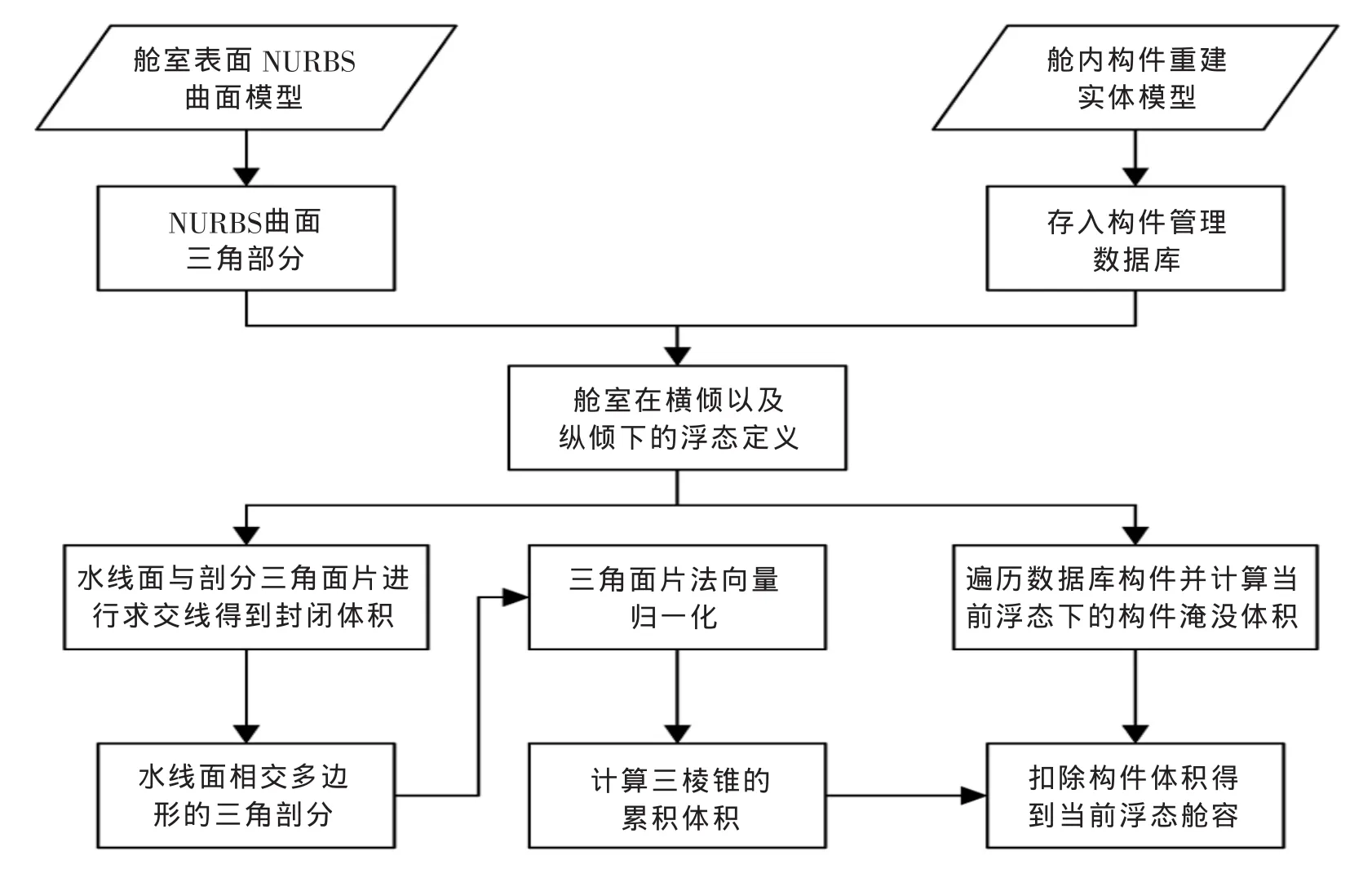
图3 基于舱室三维模型的舱室舱容计量流程

2.1 曲面模型三角剖分

为了计算舱室在不同液面高下的体积，曲面模型的三角剖分是本舱容计量方法中非常重要的一个环节，主要包括三个方面的剖分内容：

1）舱室表面NURBS曲面的三角剖分；

2）相交水线面多边形的三角剖分；

3）与水线面相交的三角面片剖分。

对于NURBS曲面三角网格剖分算法，采用映射法来对船体曲面进行三角剖分［7］。首先在U、V方向根据其参数方程按德布尔递推公式按一定间隔 （可根据舱室大小设定）进行插值形成四边格网，然后对每个四边格网剖分为两个三角格网即可。水线面与舱室表面剖分三角网相交会形成相交水线面多边形。对于平面域的三角剖分，采用Delaunay三角剖分算法。由于Delaunay三角剖分算法仅适用于平面凸集或特殊的非凸平面域。对于在实际应用中遇到的任意形状平面域，处理方法为：对非凸区域，先将凹域分割为多个凸域，分别三角化之后再缝合起来；对多连通域，添加辅助线使多连通域的三角剖分转化为单连通域的三角剖分。另外，当舱室表面剖分三角面片与给定任意高度水线面求交时，与水线面相交三角形会被分割，需按6种不同情况进行三角面片剖分［8］。

2.2 水线面以及浮态定义

船舶在静水中平衡时，其与静水平面的相对位置称为船舶的浮态［9］。船舶的浮态有正浮状态和非正浮状态，其中非正浮状态又叫自由浮态。存在吃水差相当于船舱存在一个纵向倾角。船的左右不平衡产生倾斜，由倾斜角度表示，称为横倾。船舱的横倾和纵倾状态都称为自由浮态。由于在进行水线面与舱室模型剖分三角网相交以及体积计算时，水线面高度始终为相对于舱内计量管的读数，即相对于舱室局部坐标系而言，而舱室横倾和纵倾是相对于全局静水坐标系而言的，因而需要通过同时建立舱室局部坐标系以及全局静水坐标系来定义舱室浮态，以便进行严密的舱容计量。舱室浮态定义示意图如图4所示。

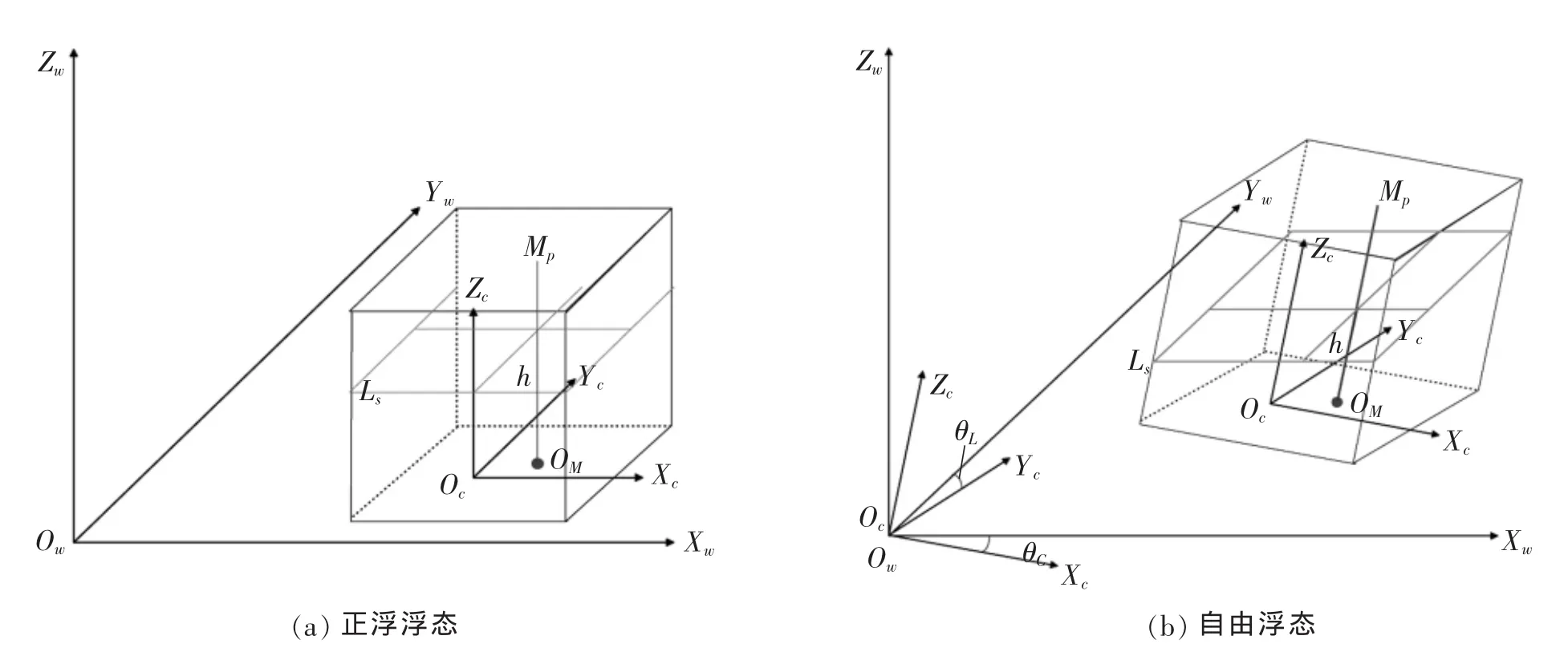
图4 舱室浮态定义

在图 4（a）中，Oc-XcYcZc为舱室局部坐标系，Mp为舱室计量管，OM为舱室计量管的固定点，Ls为舱室液面，h为液面高，Ow-XwYwZw为全局静水坐标系。在正浮状态下，为了计算一定液面高h时的舱容，首先必须先定义舱室局部坐标系（一般可由舱室底部的三个不共线点定义）及静水全局坐标系（可与正浮时的舱室局部坐标系等同），然后将舱室模型（包括构件模型）转换到局部坐标系下，最后进行舱容计算。为了计算自由浮态下的舱容［如图4（b），此时存在θL的纵倾角θC以及的横倾角］，需要首先将舱室模型以及量测液高转换到静水全局坐标系下，然后可用与正浮浮态下的同样方法进行体积计算。

2.3 三棱锥积分计算

在求出了船体曲面与任意高度水线的所有交点后，可根据线段的空间位置关系将所有线段连接成首尾相接的闭合曲线，形成水线面多边形，并与舱室其他三角面形成封闭区域（高度不高于水线面高度的所有三角面）。在计算由三角剖分面片所形成的封闭区域体积时，可将曲面上的三个顶点与坐标原点相连构成三棱锥，然后通过计算所有三棱锥来计算舱室体积。分割三棱锥的体积计算如式（1）所示。

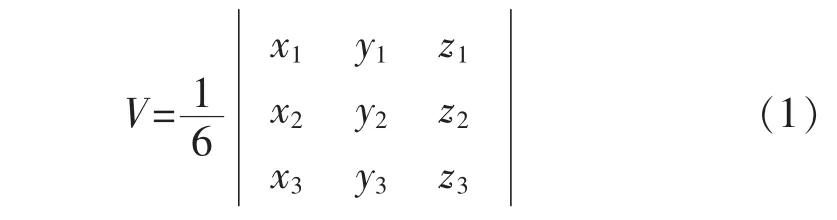
计算三棱锥体积时，首先需通过法向量归一化使得舱室表面三角面片的法向量指向一致朝外，然后判断三角面片法向量与起算点和三角面片重心所构成的向量之间的方向余弦（图5）：若方向余弦为负，则三棱锥体积为正；反之亦然。

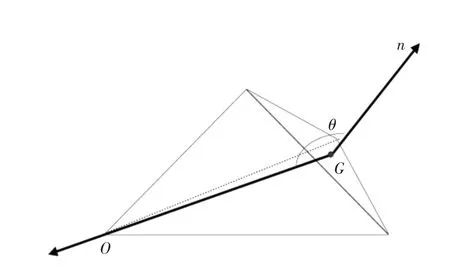
图5 三棱锥体积正负的判断

3 舱容计量试验和分析

为了实现本文所提出的舱容计量方法，以AutoCAD作为二次开发平台，利用ObjectARX二次开发工具，在Windows操作系统环境下基于VS2008语言开发了一套舱室三维重建模型的舱容计量系统。根据前述计量要求，该系统主要提供有IGES接口功能用于将在PolyWorks中生成的舱室NURBS曲面模型导入到AutoCAD数据库中以便于后期的三角剖分及舱容计量。舱室构件重建和自定义绘制功能、构件管理和构件体积计算功能以及舱容计量输出等功能。程序运行界面如图6所示。

图6 基于舱室三维重建模型的舱容计量系统

为了验证本文所提出的舱容计量方法的准确性及可靠性，以某一舱室为试验对象进行舱容计量计算，并与标准舱容检定结果相比较，部分容积比较结果如表1所示。

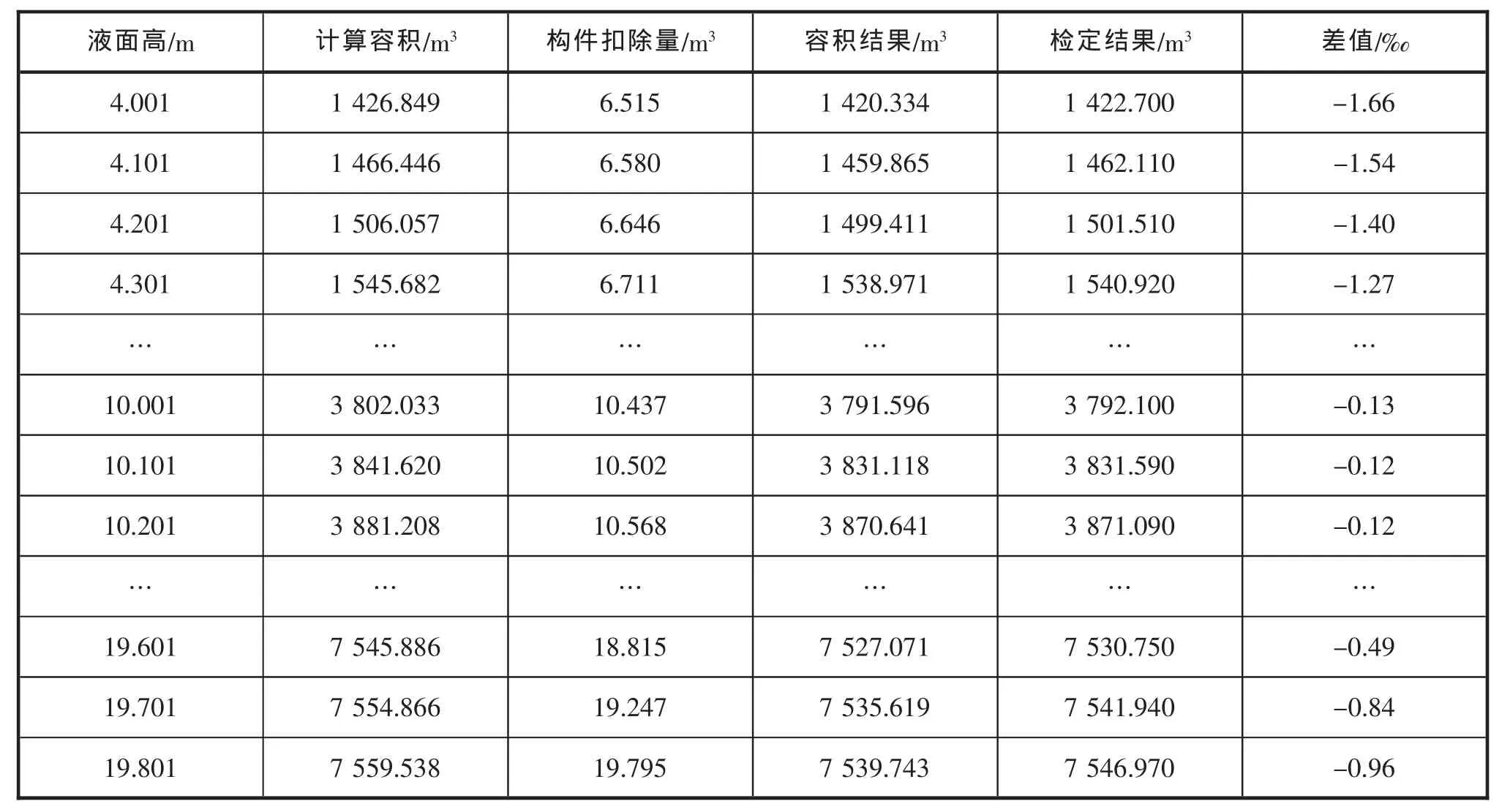
表1 容积比较表

从表1中的舱容计量比较结果来看，利用本文的舱容计量方法和标准舱容检定方法进行比对，其计量相对误差能够保持在2‰以内，满足了｜ya-yb｜≤U。通过试验证明了本方法是高效可行的。

4 结语

本文针对传统舱容计量方法的缺点，以近年来发展迅速的地面三维激光扫描测量为技术背景，提出了一种基于舱室三维重建曲面模型的舱容计量技术。该方法通过基于点云的模型重建方法，能够快速可靠地获取舱室高精度重建模型，并基于重建模型通过三角剖分以及体积积分的思想能够进行高精度高效率的舱容计量工作。另外，舱室模型不仅仅可应用于舱容实时计量，而且对于船体的修复、改造等工作具有非常重要的意义。

［1］周金河，曹光浩，熊鸿文．船舶液货计量舱容量测量不确定度分析—容积比较法［J］．交通标准化，2004，（12）：19-23.

［2］Eck M，Hoppe H. Automatic reconstruction of B-spline surfaces ofarbitrary topological type［A］.Computer Graphics（SIGGRAPH’96Proceedings）［C］.1996，30：325-333.

［3］Piegl L.On NURBS： A Survey［J］.IEEEComputerGraphics and Application，1991，11（1）：55-71.

［4］项勇．船舶舱舱容测量与修正研究［D］．武汉：武汉理工大学，2006.

［5］Tahir Rabbani Shah.Automatic reconstruction of industrial installations using point clouds and images［J］.Publications on Geodesy 62，Delft，2006.

［6］张红，赵翠莲，杨华龙，等．基于模型结构树的船内构件管理的研究［J］．计算机辅助工程，2004，13（3）：42-45.

［7］徐松，王剑英．曲面的自适应三角网格剖分［J］．计算机辅助设计与图形学学报，2000，12（4）：267-271.

［8］周燕芳．液化石油气天然气船货舱容量计量系统研究［D］．武汉：武汉大学，2010.

［9］陆从红．基于NURBS表达的船舶初步设计关键技术研究［D］．大连：大连理工大学，2005.