一种用于电力系统电压稳定分析的雅可比矩阵关键特征值算法
周陶宏,李宏仲,郑 健
(1.上海市电力公司,上海 200122;2.上海电力学院电力与自动化工程学院,上海 200090)
0 引言
采用霍普夫(Hopf)分岔理论分析电力系统电压的稳定性,必须准确求解霍普夫分岔点的位置,特别是确定最先发生穿越虚轴现象的共轭特征值,即关键特征值。
George分别利用牛顿法、幂法、反幂法和Rayleigh商迭代法来计算占主导地位的关键特征值,并对这些计算方法的鲁棒性和计算效率分别进行了对比[1-2];文献[3]利用改进的矩阵变换法来求解大规模系统动态模型的关键特征值;文献[4]则进一步提出了利用基于多处理器的并行算法来提高计算效率;L.Wang等人提出了充分利用增广矩阵稀疏特性的计算方法[5];文献[6]和文献[7]分别提出了一种对矩阵的特征值进行连续追踪的方法,Xiaoyu Wen等人将该方法引入了电力系统的稳定研究中,提出了一种追踪关键特征值的连续法[8]。
本文将在这些计算方法的基础上做进一步的分析与研究。首先,利用特征值实部、特征值关于分岔参数的一阶和二阶灵敏度系数,构造一个能够判断关键特征值的指标,然后直接利用连续性方法,对关键特征值进行连续追踪,直至霍普夫分岔点。
1 特征值连续追踪的基本步骤
对于某一不对称矩阵J(μ),以及该矩阵的某一特征值λ(μ),假设J(μ)和λ(μ)均为某一参数μ的连续函数,令w和v分别为λ对应的左特征向量和右特征向量,则:
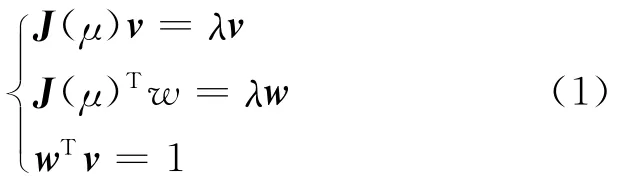
等式两边对参数μ求导并整理:
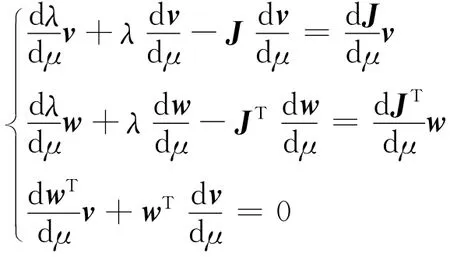
由于:
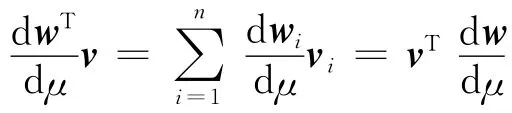
得到:
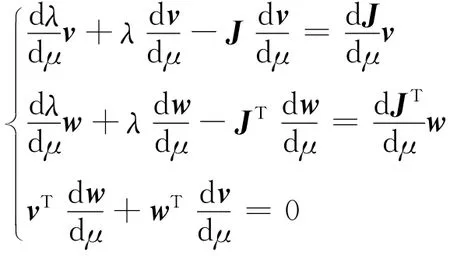
写成矩阵形式:
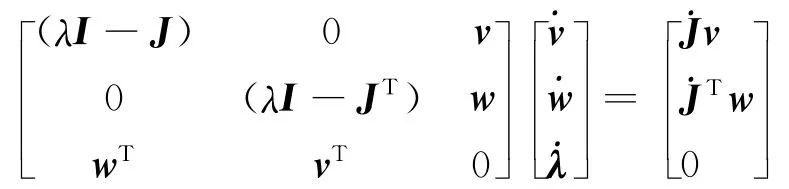
将μ视为变化因子,结合龙格-库塔法就可以对特征值λ进行追踪,并且可以得到λ关于μ的变化曲线。
对于电力系统的DAE模型:
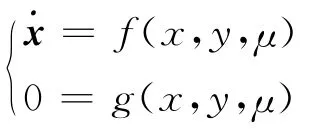
经过线性化处理后:

式中:A=Dxf(x,y);B=Dyf(x,y);C=Dxg(x,y);D=Dyg(x,y)。
由于矩阵A、B、C、D可以视为参数μ的函数(这里μ为分岔控制参数,即负荷增长控制参数),因此,系统雅可比矩阵则可写为:
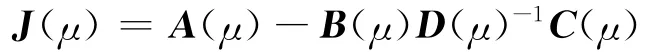
显然,矩阵J基本上失去了稀疏性,因此本文将给出直接利用稀疏矩阵A、B、C、D追踪λ变化曲线的表达式。
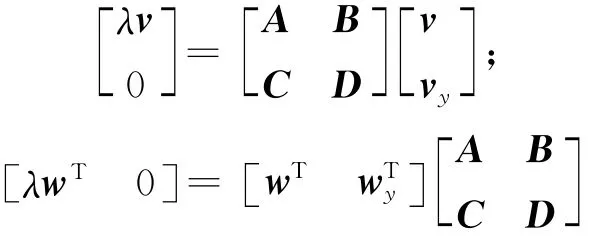
式中:wy和vy分别是对应特征向量的拓展部分。
对于某一特征值λ,对应的左右特征向量分别表示为w、v:
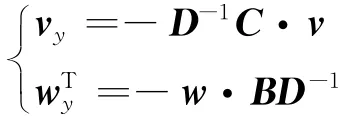
套用式(1)的形式得到:
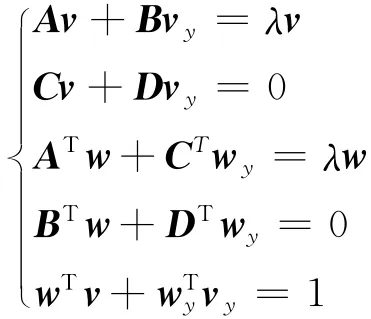
对两边求导:

整理并写成矩阵形式:
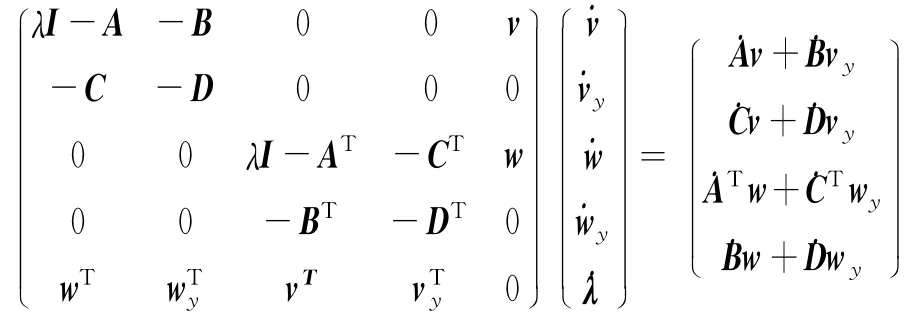
如果状态变量个数为m,代数变量个数为n,则有向量:
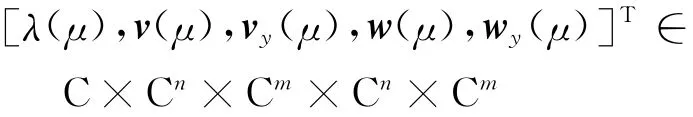
定义:
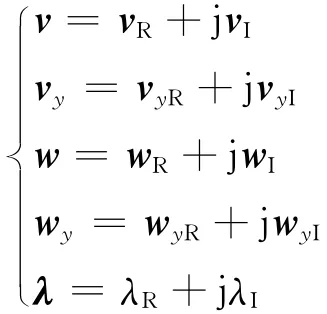
式中:
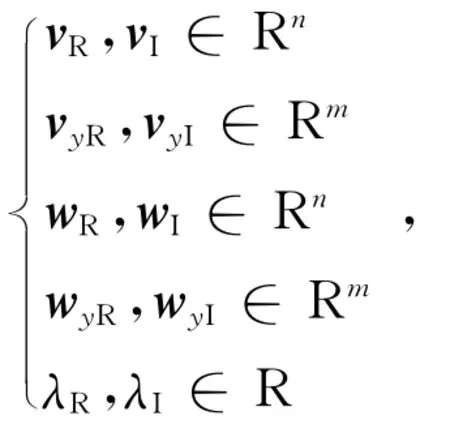
可以拓展为:

式中:
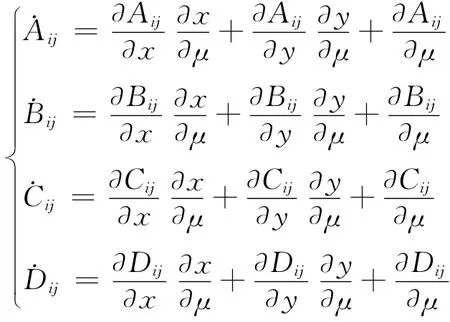
式中:下标ij表示该元素为矩阵的第i行、第j列元素。
从理论上讲,利用式(2)可以对感兴趣的任意一个特征值从初始状态开始进行连续跟踪,但是为了提高精确度,将利用连续性方法对系统平衡解流形进行连续追踪。当平衡解流形比较靠近霍普夫分岔时,再转入对关键特征值的连续追踪。
2 关键特征值的选择
关键特征值指得是随着分岔控制参数μ的变化,实部最先变为零的一对共轭特征值:
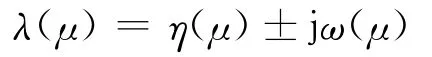
当关键特征值的实部穿越虚轴时,意味着系统运行到了霍普夫分岔点,此时系统的平衡解不能保持稳定,会出现振荡性现象。而在利用连续法求解霍普夫分岔点的追踪过程中,对于系统的每个平衡解都可以求解出系统雅可比矩阵的全部特征值中实部比较靠近虚轴的部分特征值。但在准确追踪到霍普夫分岔点之前,无法准确地确定到底哪一个特征值是最终引发霍普夫分岔的关键特征值,因此需要在追踪过程的每一步计算中根据一定的判断标准,从求得的实部绝对值较小(即比较靠近虚轴)的特征值λ(μ)中再选取一小部分,做为准关键特征值进行深入分析比较。
特征值的实部η(μ)可以做为一种判断标准,实部越靠近虚轴说明其出现霍普夫分岔的可能性越大。但是随着负荷的增长,在前一个平衡点相对离虚轴较远的特征值,可能在下一个平衡点距离虚轴就会变得比较近,也就是说随着负荷的增长,特征值实部的变化率是各不相同的。由此,文献[8]提出利用特征值实部对实部关于负荷增长的一阶灵敏度系数的比值η(μ)/(∂η(μ)/∂μ)做为判断标准。即在判断关键特征值时考虑特征值实部的变化情况,将特征值实部较小而且变化幅度又比较大的特征值视为关键特征值。而文献[9]指出,在平衡点接近霍普夫分岔点的时候,随着负荷的增长,关键特征值的实部大小可能会发生突变,此时仅通过判断一阶灵敏度系数难以准确地确定关键特征值。为此,本文提出利用特征值实部大小η(μ)、特征值实部关于负荷增长的一阶灵敏度系数∂η/∂μ和二阶灵敏度系数∂2η/∂μ2来综合判断关键特征值,同时参考速度、加速度与位移的关系表达式给出评判标准的计算表达式。一阶和二阶灵敏度系数的计算方法详见文献[8]和文献[9]。
对于匀加速度运动,假设物体的位移为S,初始速度为v0,加速度为a,物体完成位移S所需的时间为t,则有:
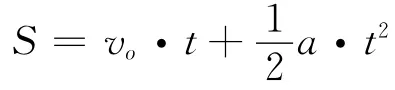
得到时间:
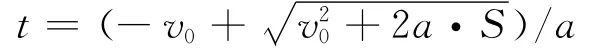
如果将特征值实部绝对值|η(μ)|视为“位移”,特征值实部关于负荷增长的一阶灵敏度系数∂η/∂μ视为“初始速度”,即随着负荷做单位增长,特征值实部的相应变化量。如果∂η/∂μ大于0,说明随着负荷的增长,特征值实部η(μ)逐渐增大,假设系统未达到霍普夫分岔点之前,系统的平衡点为稳定的平衡点,此时所有特征值实部应该小于零。那么∂η/∂μ大于0就意味着随着分岔控制参数μ的增大,该特征值实部是趋近于虚轴的,反之则该特征值远离虚轴。
进一步的将特征值实部关于负荷增长的二阶灵敏度系数∂2η/∂μ2视为“加速度”,那么如果∂2η/∂μ2大于0就意味着随着分岔控制参数μ的增大,∂η/∂μ是逐步增大的,也就是说随着分岔控制参数μ的增大,该特征值实部靠近虚轴的趋势在逐步加大;换言之,当负荷增长时该特征值的实部接近虚轴的“速度”在逐步增大。由此,可以构造判断关键特征值的指标如下:
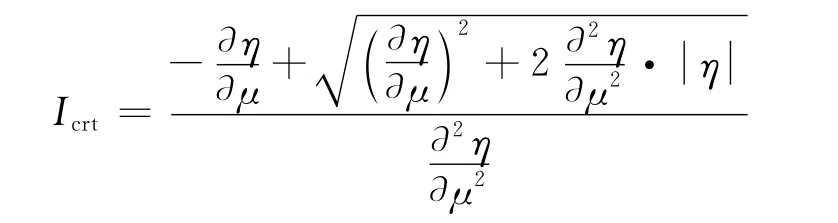
很显然,当特征值实部η(μ)绝对值较小、特征值实部关于负荷增长的一阶灵敏度系数∂η/∂μ和二阶灵敏度系数∂2η/∂μ2都比较大的情况下,Icrt的值比较小。这就意味着该特征值由于本身就比较接近虚轴,而且随着负荷的增长实部绝对值减小的趋势比较快,因此该特征值最有可能发生穿越虚轴的情况。利用该指标可以判断哪一个特征值是关键特征值,在每一步计算中所得的特征值中,Icrt值最小的即视为关键特征值(对应的指标即Icrtmin)。由于Icrt的计算过程中用到了特征值实部η(μ)、一阶灵敏度系数∂η/∂μ和二阶灵敏度系数∂2η/∂μ2的大小,从而充分的计及了特征值当前状态和特征值随着负荷增长的变化趋势,因此其指示性较好,能够对特征值逼近虚轴的态势给出定量的分析。
为了提高计算的可靠性,根据追踪平衡解流形的最后一步计算结果,对特征值按照Icrt值由小到大的顺序进行排序,选择排在前面的几个特征值分别进行连续追踪。
3 算法步骤
为了求解结果必须先确定追踪步长。在计算过程中假设初始步长为h0,首先计算初始状态下系统的雅可比矩阵的关键特征值及一阶灵敏度系数∂η/∂μ和二阶灵敏度系数∂2η/∂μ2,并计算Icrt,min,0,即关键特征值对应的指标Icrt值;然后执行龙格库塔法完成一步计算;在第二步计算过程中,首先求出关键特征值一阶和二阶灵敏度系数,最后计算出Icrt,min,1。步长h1采用下式确定:
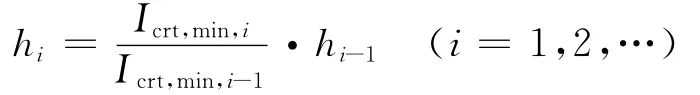
追踪关键特征值的混合方法的计算步骤:
(1)利用常规连续性方法追踪系统的平衡解流形,直至平衡解流形比较靠近霍普夫分岔时(Icrt,min的值小于某一预先设定的值);
(2)根据研究的需要利用Icrt的大小确定进行连续跟踪的特征值;
(3)设定一个极小值ε用于判定是否出现特征值实部穿越虚轴的现象;
(4)形成计算式(3)所需的矩阵;
(5)完成一步龙格-库塔计算;
(6)判断所追踪特征值的实部是否小于ε,如果小于则停止计算,否则转到步骤(7);
(7)求出∂η/∂μ和∂2η/∂μ2,并进一步求出I crt,min,1;
(8)确定步长hi;
(9)完成一步龙格-库塔计算;
(10)修正计算所需的矩阵,转到步骤(6)。
4 算例分析
以New-England 39节点系统为例,验证所提方法的有效性。先从初始状态开始利用常规连续性算法追踪平衡解流形,当Icrt,min小于0.15时,转入对关键特征值的连续追踪。表1给出了追踪特征值的初始状态。选表中Icrt值最小的一对共轭特征值进行连续追踪,h0选0.018。
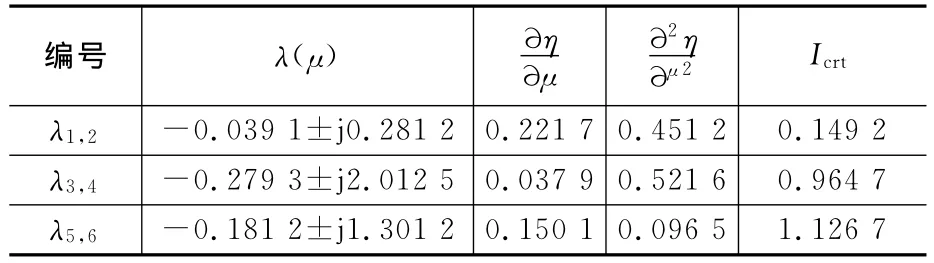
表1 部分特征值灵敏度系数
图1给出了所追踪的共轭特征值实部的变化,随着负荷控制参数变化,特征值λ1,2在总负荷增量为791 MW左右时出现穿越虚轴的情况,从而出现霍普夫分岔,此时系统将可能出现振荡性失稳现象。
从理论上讲,利用本文方法可以对任何感兴趣的特征值进行追踪,但是只有通过追踪关键特征值才能确定霍普夫分岔点的位置。为了进一步说明这一问题,同样对特征值λ3,4和特征值λ5,6进行追踪,图2和图3给出了这两对共轭特征值实部的变化曲线。
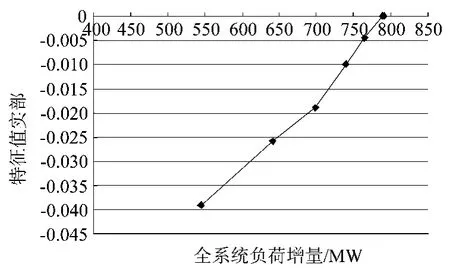
图1 特征值λ1,2的η(μ)变化曲线图
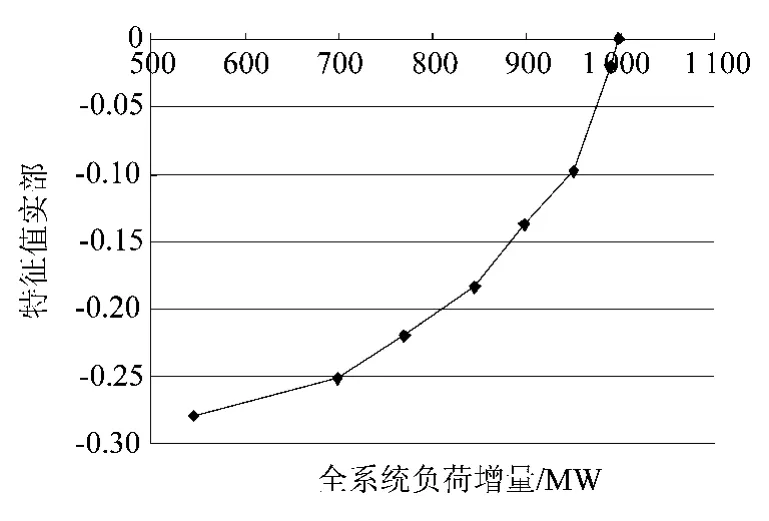
图2 特征值λ3,4的η(μ)变化曲线图
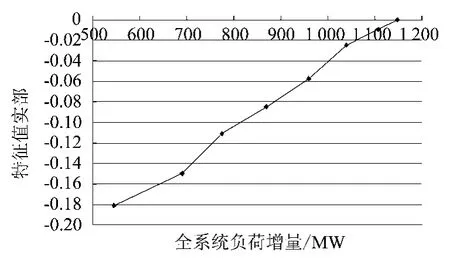
图3 特征值λ5,6的η(μ)变化曲线图
结果表明,当这两对共轭特征值实部为零时,系统的负荷增量大于791 MW。即这两对共轭特征值不是最先穿越虚轴的关键特征值。同时也说明了指标Icrt具有较高的指示性,能够比较准确的确定出关键特征值。通过追踪该特征值得到的霍普夫分岔点是准确的。
5 结语
提出了一种追踪关键特征值的混合方法。该方法将追踪平衡解流形的连续方法同关键特征值连续追踪方法结合起来,先从初始状态开始追踪平衡解流形,当平衡解靠近霍普夫分岔点时,利用判断关键特征值的指标Icrt来确定最有可能发生穿越虚轴现象的关键特征值并对其进行连续跟踪,由于Icrt的计算过程中计及了特征值当前状态和特征值随着负荷增长的变化趋势,能够较为准确的判定关键特征值,并可利用Icrt来辅助确定跟踪步长的大小。利用该方法对New England 39节点系统进行计算,得到了引起霍普夫分岔现象的关键特征值的具体变化曲线。
[1] Semlyen A,Wang L.Sequential Computation of the Complete Eigensystem for the Study Zone in Small Signal Stability Analysis of Large Power Systems[J].IEEE Trans.on Power System,1988,3(2):715-725.
[2] George Angelidis,Adam Semlyen.Improved Methodologies for the Calculation of Critical Eigenvalues in Small Signal Stability Analysis[J].IEEE Trans.on Power Systems,1996,11(3):1209-1217.
[3] Leonardo T G Lima,Licio H Bezerra,Carlos Tomei,et al.New Method for Fast Small-Signal Stability Assessment of Large Scale Power Systems[J].IEEE Transaction on Power System,1995,10(4):1979-1985.
[4] Jorge M Campagnolo,Nelson Martins,Jose L R Pereira,et al.Fast Small-signal Stability Assessment using Parallel Processing[J].IEEE Transaction on Power System,1993,9(2):949-956.
[5] L Wang,A Semlyen.Application of Sparse Eigenvalue Techniques to the Small Signal Stability Analysis of Large Power Systems[J].IEEE Trans.on Power Systems,1990,5(2):635-642.
[6] Robert Kalaba,Karl Spingarn,Leigh Tesfatsion.Variational Equations for the Eigenvalues and Eigenvectors of Nonsymmetric Matrices[J].Journal of Optimaization Theory and Applications,1981,33(1):1-8.
[7] Ji W,Venkatasubramanian V.Dynamics of a Minimal Power System:Invariant Tori and Quasiperiodic Motions[J].IEEE Trans.on Circuits and Systems I:Fundamental Theory and Applications,1995,42(12):981-1000.
[8] Xiaoyu Wen,Ajjarapu V.Application of a Novel Eigenvalue Trajectory Tracing Method to Identify Both Oscillatory Stability Margin and Damping Margin[J].IEEE Trans.on Power System,2006,21(2):817-824
[9] Hae-Kon Nam,Yong-Ku Kim,Kwan-Shik Shim,et al.A New Eigen-sensitivity Theory of Augmented Matrix and its Applications to Power System Stability Analysis[J].IEEE Trans.on Power Systems,2000,15(1):363-369

