两体二能级系统的纠缠特性
成耀宇,胡占宁,宁振动
(1.天津工业大学理学院,天津300160;2.天津工业大学环境科学与化学工程学院,天津300160)
纠缠是量子力学有别于经典力学的最主要原因之一,并且在早期的量子物理学中激发了许多哲学上的讨论[1]。最近,纠缠被看作量子信息处理的来源[2]。事实上,它是实现量子隐形传态、量子密码的关键因素之一[3],而且被认为是实现量子计算机的重要来源。然而,用于量子信息处理的量子体系不可避免的要与周围的环境发生相互作用,它使得量子体系由纯态变为混合态[4]。因此,分析量子体系与周围环境的相互作用而引起的纠缠衰退甚至纠缠突然死亡就成为当前的一个重要课题[5]。在单体量子系统中,这一过程被称作退相干,人们采取了许多办法来减弱这一过程[6]。具有非局域量子关联性质的多体量子系统的纠缠演化更加能引起人们的关注。 例如,纠缠突然死亡是由Yu and Eberly发现的[7],它意味着纠缠在有限的时间内消失,而且与单量子比特的相干演化有着显著的不同。这一有趣的现象可以通过纠缠的原子系综来观测到[8]。人们对纠缠和纠缠突然死亡的演化进行了分析并且得到了许多有趣的结果[9,10]。本文基于量子纠缠这一非常重要的物理概念,通过对物理模型的计算和分析,重点研究了两体二能级系统在零温玻色欧姆和零温玻色超欧姆环境下的纠缠特性。
1 纠缠度的定义
纠缠度有许多定义,如线性熵、Concurrence、Negativity等。我们将采用Wootters定义Concurrence来度量纠缠[11]。对于一个处于状态ρ的任意两体二能级系统,Concurrence定义为
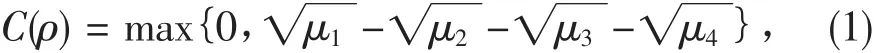
其中,μi(i=1,2,3,4)为矩阵
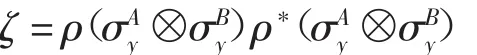
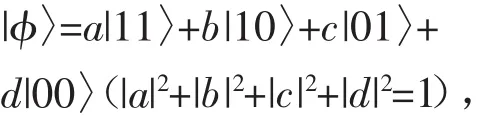
则concurrence简化为

如果系统处于混合态且密度矩阵可表示为以下形式:

则concurrence简化为[12]
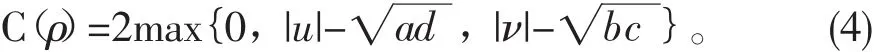
2 模型
考虑一个复合系统[13],该系统由两个相互作用并且各自都同外浴 (玻色环境)耦合的二能级系统组成。它的哈密顿量由三部分组成,两体二能级系统自由哈密顿量Hs,两体二能级系统和外浴相互作用的哈密顿量H1,外浴自由哈密顿量HB:
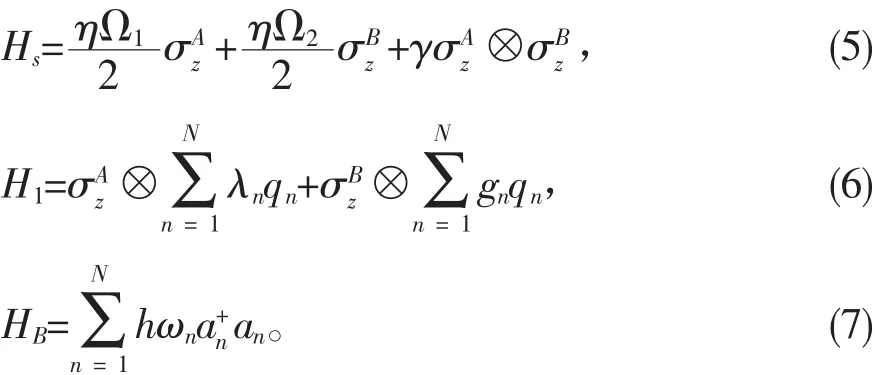
常数λn和gn是两个二能级体系分别同外浴耦合的系数,γ是两个自旋1/2粒子之间的耦合强度。假设同外浴耦合的每个二能级体系的耦合常数是不同的,对自旋A设为λn,对自旋B设为gn。
为了度量与环境相互作用的两体二能级系统的纠缠度,必须知道其随时间演化的约化密度矩阵。设两体二能级系统初态为

在弱耦合极限条件下,经过时间t的演化,其约化密度矩阵为
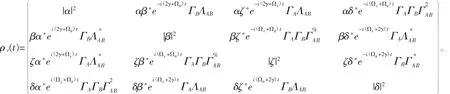
其中,消相干因子Γi(t)定义为
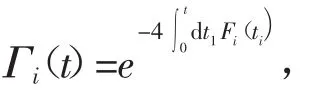
且
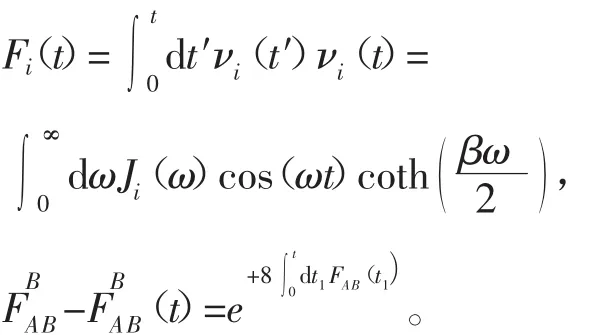
环境引起的耗散为
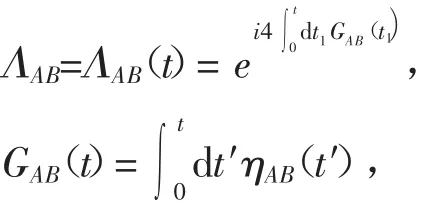
且
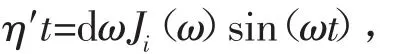
谱密度函数Ji(ω)为
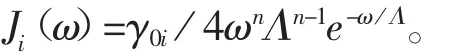
假设在零温欧姆环境下,消相干因子具有如下形式[13]:
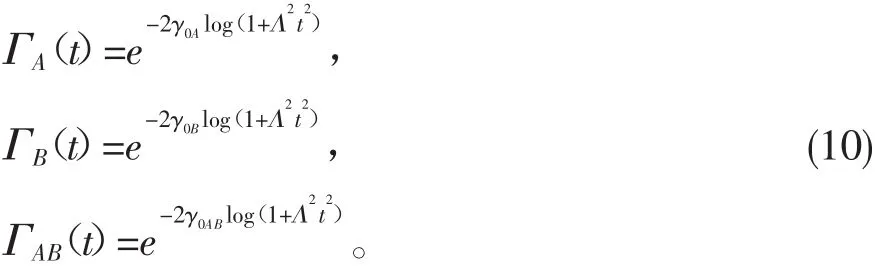
在零温超欧姆环境下,消相干因子为
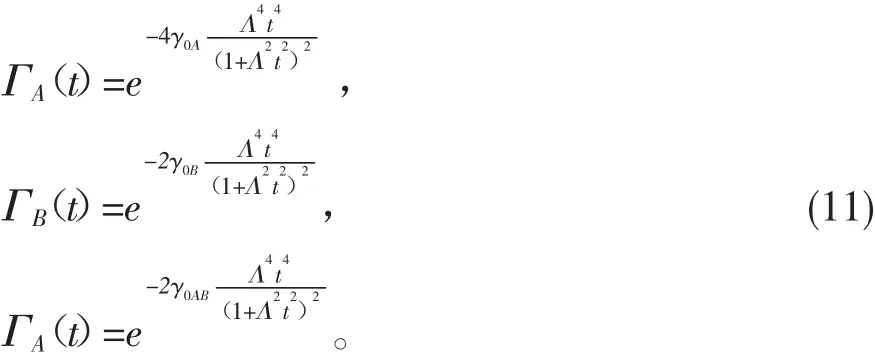
该形式与自旋-玻色模型在零温的形式类似[14],其中Λ是外浴的中断频率。
为了达到本文的目的,我们将定义一个初始密度矩阵,也称作类Werner态:

其中,r∈(0,1]表示初态的混合度,ρ是 4×4矩阵,ρ的密度矩阵表示如下:
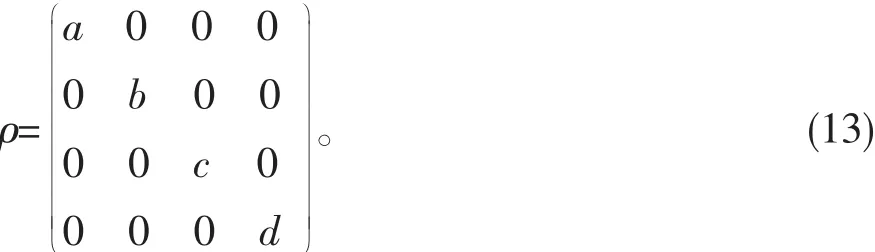
其中,a=d,b=c,且a,b,c,d都为非负实数,
|a|2+|b|2+|c|2+|d|2=1。初始态|φ〉为
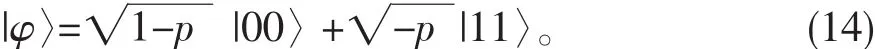
其中,p表示初态的纠缠程度,|0〉,|1〉为泡利算符σz的本征值,p=1/2时,(14)式为贝尔态。
由方程(9)~(14),我们可以得到t>0的约化密度矩阵:
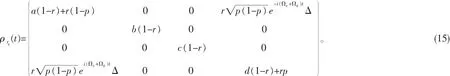
为了得到Concurrence得具体表达式我们需要计算矩阵
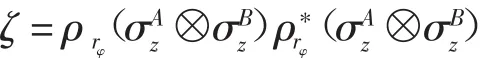
的本征值,经过计算得到其本征值:
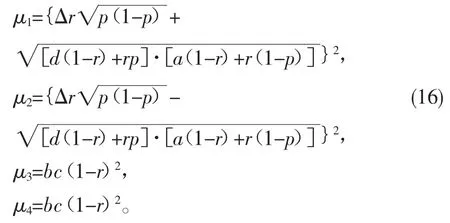
考虑初始条件可得:
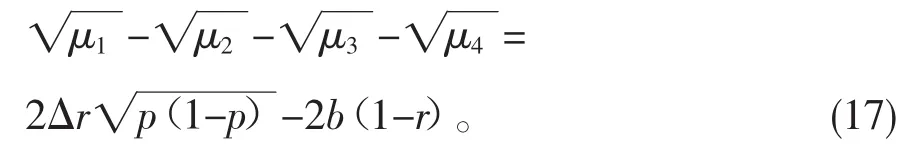
因为在零温玻色欧姆环境和零温玻色超欧姆环境下都有 γ0A=γ0B=γAB=γ0,因此,(16)式可简化为
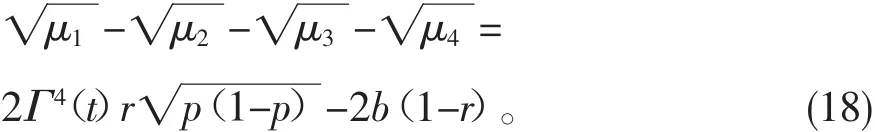
当
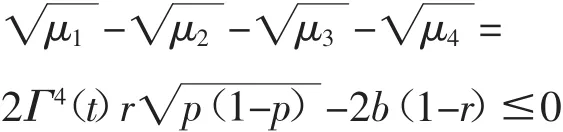
时,将会发生纠缠突然死亡现象。很明显,
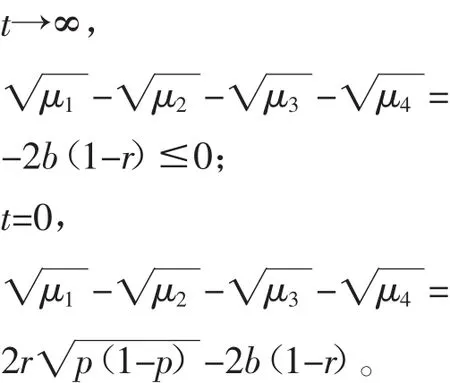
因此,如果初始态是纠缠的,那么纠缠突然死亡总是会发生。当

时,取b=1/3,则在零温玻色欧姆库环境下,(18)式可表示为
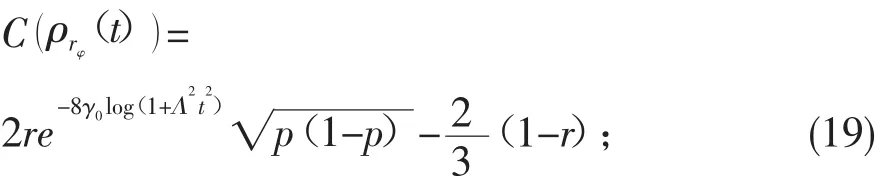
在零温玻色超欧姆库环境下,(18)式可表示为
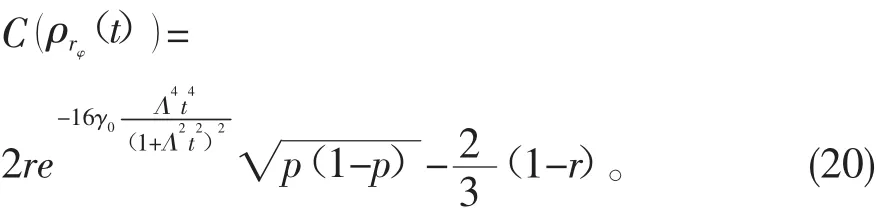
在零温玻色欧姆和零温玻色超欧姆两种环境中,两体系统纠缠度(Concurrence)的变化规律将有何异同点呢?下面就此问题展开讨论。
通过分析得到的解析解如:式(19)和式(20),从两式可以看到:两体系统纠缠度是参数t,r,p(视Λ为常数)函数。为了清晰化、直观化,我们进行了数值模拟并得到了图1~6。 其中,图1,2,3表示令参数p为定值,两体系统纠缠度随t,r的变化;图4,5,6表示令参数r为定值,两体系统纠缠度随t,p的变化。
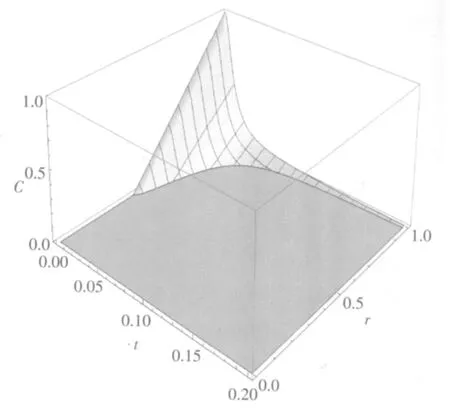
图1 当两体系统耦合了一个耦合常数为γ0=0.1的零温玻色欧姆环境时,C作为r和t的函数,Λ=100,p=0.5
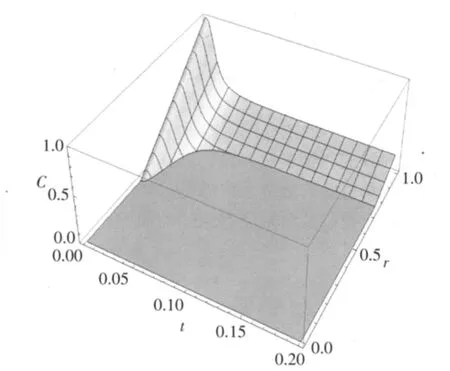
图2 当两体系统耦合了一个耦合常数为γ0=0.1的零温玻色超欧姆环境时,C作为r和t的函数,Λ=100,p=0.5
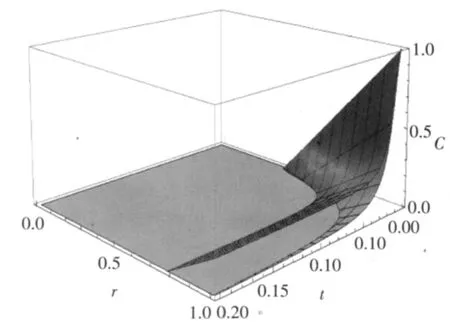
图3 上层为超欧姆环境情况,下层为欧姆环境情况
从图1、图2中可以看出,在两种环境下,均出现了纠缠突然死亡的现象;当参数r增大时,两种环境下的纠缠突然死亡的时间都会变长。图3为图1和图2的结合,可以看到,在相同条件(p和Λ一致)下,零温玻色超欧姆环境下的纠缠突然死亡时间要比零温玻色欧姆环境下的纠缠突然死亡时间长。
从图4、图5中可以看出,在两种环境下,同样都出现了纠缠突然死亡的现象;与图1、2相同,当参数p增大时,两种环境下的纠缠突然死亡的时间都会变长。图6为图4和图5的结合,我们可以看到,在相同条件(r和Λ一致)下,零温玻色超欧姆环境下的纠缠突然死亡时间要比零温玻色欧姆环境下的纠缠突然死亡时间长。
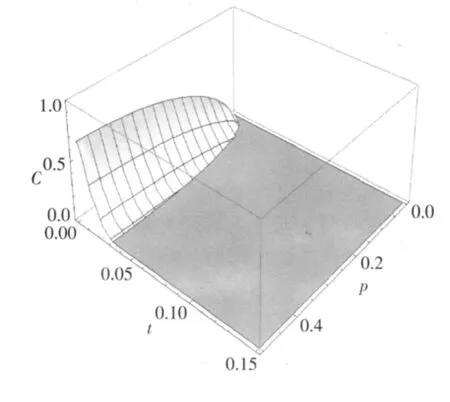
图4 当两体系统耦合了一个耦合常数为γ0=0.1的零温玻色欧姆环境时,C作为p和t的函数,Λ=100,r=0.8
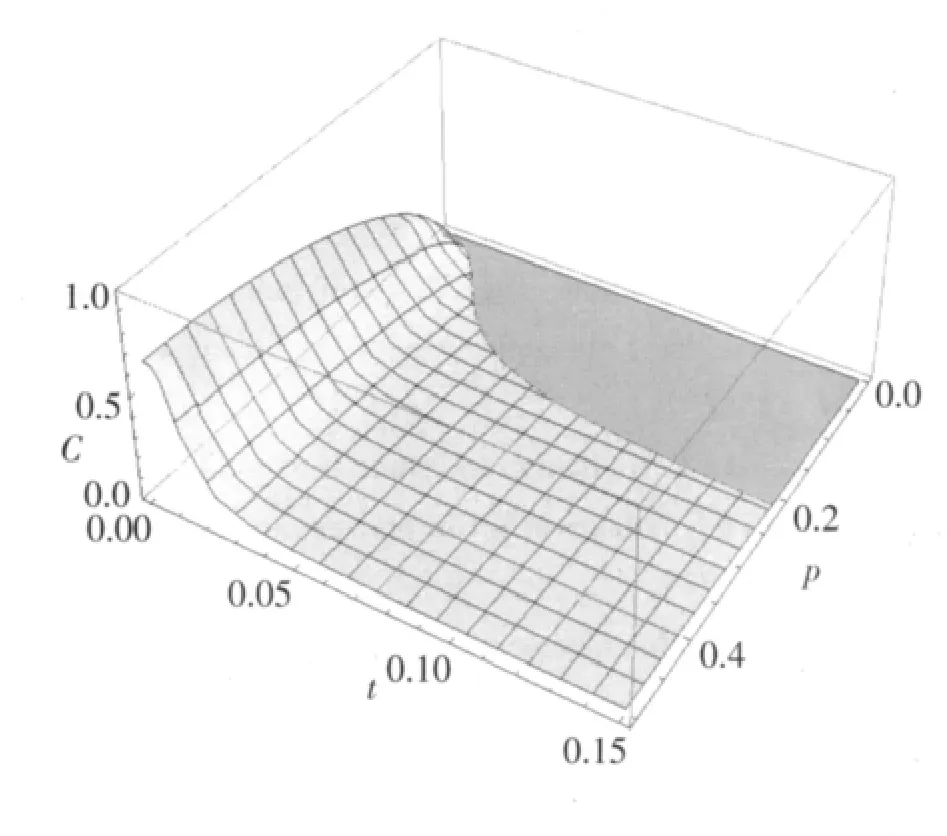
图5 当两体系统耦合了一个耦合常数为γ0=0.1的零温玻色超欧姆环境时,C作为p和t的函数,Λ=100,r=0.8
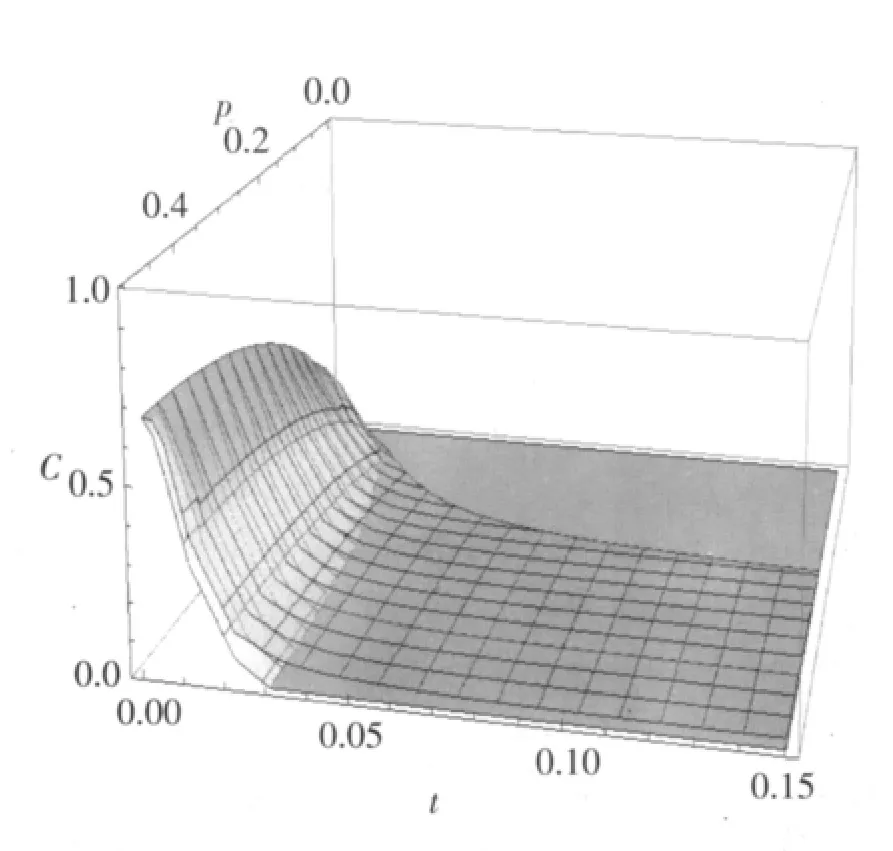
图6 上层为超欧姆环境情况,下层为欧姆环境情况
通过以上分析,我们可以看到参数r,p对两体系统纠缠突然死亡时间的影响基本保持一致,也就是说零温玻色超欧姆环境下的纠缠突然死亡时间要比零温玻色欧姆环境下的纠缠突然死亡时间长。
3 结论
分析了在零温玻色欧姆环境和零温玻色超欧姆环境的下两体二能级系统的纠缠特性,并得到了上述结果。但我们最终的目的是要调控和保护纠缠,并使其能够运用于现实环境,因为它是实现量子计算机的重要来源。尽管我们注意到许多关于纠缠调控和保护所取得的进展,但是许多基础的困难仍然存在,其中最主要的困难就是系统与环境相互作用而导致的纠缠突然死亡。本文最主要的结果就是通过一些特殊的环境来帮助延迟纠缠突然死亡的时间。希望我们的结果能对纠缠的调控和保护研究做出一点贡献。
[1]Einstein A,Podolsky B,Rosen R.Can Quantum-Mechanical Description of Physical Reality Be Considered Complete[J].Phys Rev,1935,47:777-780.
[2]Nielsen M A,Chuang I L.Quantum Computation and Quantum Information[M].Cambridge:Cambridge University Press,2000:571-581.
[3]Ekert A K.Quantum cryptography based on Bell′s theorem[J].Phys Rev lett,1991,67(6):661-663.
[4]Breuer H P,Petruccione F.The Theory of Open Quantum Systems[M].Oxford:Oxford University Press,2002:421-431.
[5]Weiss U.Quantum Dissipative Systems(Second Edition)[M].Singapore:World Scientific Publishing,1999:355-367.
[6]Cui W,Xi Z R,Pan Y.Optimal decoherence control in non-Markovian open dissipative quantum systems[J].Phys Rev A,2008,77:032117-032128.
[7]Yu T,Eberly J H.Finite-Time Disentanglrment Via Spontaneous Emission[J].Phys Rev Lett,2004,93:140404-140407.
[8]Laurat J.Heralded Entanglement between Atomic Ensembles:Preparation,Decoherence,and Scaling[J].Phys Rev Lett,2007,99:180504-180507.
[9]Dajka J,Luczka J.Origination and survival of qudit-qudit entanglement in open systems[J].Phys Rev A,2008,77:062303-062309.
[10]Ikram M,Li F L,Zubairy M S.Disentanglement in a two-qubit system subjected to dissipation environments[J].Phys Rev A,2007,75:062336-062344.
[11]Wootters W K.Entanglement of Formation of an Arbitrary State of Two Qubits[J].Phys Rev Lett,1998,80:2245-2248.
[12]LI Zhi-jjan,LI Jun-qi,JIN Yan-hong,et al.Time Evolution and Transfer of Entanglement Between an Isolated Atom and a Jaynes-Cummings Atom[J].J Phys B At Mol Opt Phys,2007,40:3401-3411.
[13]Lombardo F C,Villar P I.Environmentally induced effects on a bipartite two-level system:Geometric phase and entanglement properties[J].Phys Rev A,2010,81:022115-022118.
[14]Lombardo F C,Villar P I.Geometric phases in open systems:A model to study how they are corrected by decoherence[J].Phys Rev A,2006,74:042311-142314.

