船舶动力定位系统数学模型参数辨识方法研究

李文华杜佳璐张银东宋健孙玉清陈海泉

（1.大连海事大学轮机工程学院 大连 116026；2.大连海事大学信息科学技术学院 大连 116026）

船舶动力定位系统数学模型参数辨识方法研究

李文华1杜佳璐2张银东1宋健1孙玉清1陈海泉1

（1.大连海事大学轮机工程学院 大连 116026；2.大连海事大学信息科学技术学院 大连 116026）

船舶动力定位是深海开发的关键技术之一，随着海上油气生产向深海的发展，对应用于船舶动力定位系统的船舶数学建模也提出更高的要求。首先介绍船舶动力定位系统的意义及其应用的数学模型，然后针对船舶及推进器动力学数学模型的辨识与建立过程进行详细介绍，最后讨论船舶外界环境扰动建模的策略。

船舶；动力定位系统；数学模型；辨识；环境扰动

0 引言

船舶动力定位技术是指在不借助锚泊系统的情况下，使船舶利用自身的推进装置抵御风、浪、流等外界扰动的影响，以一定的姿态保持在海面某目标位置或精确地跟踪某一给定轨迹，以完成各种作业功能［1］。它具有定位成本不随着水深增加而增加，机动性强，操作简便，定位精度高，不破坏海床等优点，故被广泛应用于海洋石油钻井平台以及打捞救助船、工程供应船、消防船等各种船舶上，是维持海洋浮式作业平台和船舶正常工作的关键。近年来，随着海洋开发不断向着远海、深海扩展，动力定位技术对海洋开发具有越来越重要的现实意义，已受到业界广泛关注［2-3］。

为了提高动力定位船舶的操纵性能与定位精度，必须建立一个尽量精确而全面的数学模型。应用于动力定位系统的船舶数学模型可以分为船舶及推进器动力学数学模型、船舶外界环境干扰因素环境扰动模型两个部分。

1 船舶动力定位系统数学模型

在有风、浪、流共同作用的复杂海况下，无约束的船舶具有六个自由度的运动特征。这些运动均含有低频分量和高频分量。低频运动分量可以认为是由螺旋桨的推力、舵力、流力、风力和缓变的波浪漂移力等产生的；高频运动分量主要是由波浪引起的一阶波频运动响应，随波浪的起伏而往复，呈现出自动恢复原位的特性。水面船舶动力定位主要控制水平面的三个自由度运动，即纵荡、横荡、艏摇［4］。

为了描述船舶在水平面的运动，必须建立两个坐标系统，如图1所示。一个是大地坐标系XEOYE，另一个是随船坐标系XOY。

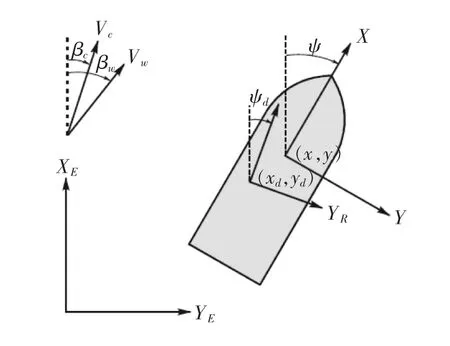
图1 大地坐标系与随船坐标系

两个坐标系的Z轴均向上，XY平面与静水面重合，船舶低频运动方程就是建立在随船坐标系XOY中。在每个采样周期中，均要通过这两个坐标系的转换来进行速度、位置及控制力的估算和估计。位置向量η=［x，y，ψ］T定义大地坐标系下的船舶位置（x，y）和艏摇角ψ，速度向量υ=［u，v，r］T定义随船坐标系下的船舶纵荡、横荡和艏摇角速度，其中转换矩阵为：

式中：R为旋转矩阵，被定义为

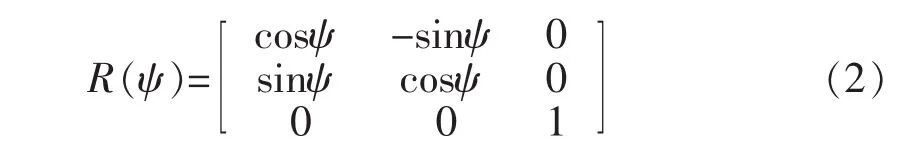
根据船舶操纵性理论及动力定位系统的特性，采用如下的非线性运动方程作为系统模型［5］：

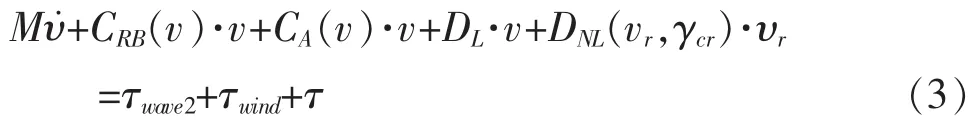
式中：M为船舶惯性矩；

CRB为船舶刚体科里奥利及离心力矩阵；

CA为船舶附加质量科里奥利及离心力矩阵；

DL为线性水动力阻尼矩阵；

DNL为非线性水动力阻尼矩阵；

τwave2、τwind和τ则分别为波浪漂力、风力和推进器控制力矩阵。

2 船舶数学模型参数辨识

2.1 船舶模型辨识方法

国外应用于船舶动力定位系统的船舶数学模型研究早在20世纪60年代就已开始。第一代船舶模型使用的是线性化模型，控制参数选择的困难直接导致了单输入/单输出PID控制器的功效很低。当时，Balchen及其合作者把基于多变量的线性最优化控制和Kalman滤波理论的控制方法引入动力定位系统，由此诞生了第二代动力定位系统。船舶数学模型方面的进步体现在：将系统动力学模型分为高频子系统和低频子系统两部分，分别描述船舶的高频运动和低频运动［6］。为避免不必要的能量浪费和推进器磨损，仅对低频运动加以控制而忽略高频部分运动［7］。但由于船舶是一个复杂的非线性系统，使用线性模型必然将使船舶的控制效果降低。因而非线性控制理论在动力定位系统中的应用成为了研究热点。

非线性控制船舶数学模型最初都是假设海浪滤波模型参数在操作中不变，而这明显是不现实的。因为实际上海况是不断变化的，而且变化范围相当大，因此需要更科学的建模以根据变化的海况重新构造船舶的低频运动。在文献［8］中提出对非线性无源观测器进行了扩展。文献［9］中，通过在观测器中增益规划海浪滤波模型参数，自动地适应当前的海况，给出位置、速度和慢变的环境扰动精确估值，并用于非线性PID控制律。文献［10］考虑到船舶实际航行中水动力参数的变化，基于构造性的Lyapunov直接法，设计输出反馈动力定位控制器，使船舶最终全局收敛于期望位置，这样的鲁棒自适应控制是一大突破。

针对动力定位技术的发展，我国研究人员也进行了积极有益的探索。文献［11］用固定增益的卡尔曼滤波估计低频运动，而高频运动则用一个参数模型来模拟，并用递推增广最小二乘法来估计参数，从而估计出船舶的高频运动。通过控制计算和模拟试验，取得了良好的效果。文献［12］提出了水面舰船动力定位控制系统模型参数的离线最速下降寻优的辨识方法，提高了动力定位系统研制过程的工作效率。文献［13］在建立船舶三维几何模型基础上，对满载船舶从浅水40 m到深水5 000 m的水动力系数进行数值计算。利用三维线性势流理论，在频域里研究船舶在浅水中的辐射问题，应用三维源汇分布法对不同水深下船舶运动的水动力系数，包括附加质量和阻尼系数进行数值计算与分析，得出了有限深水域的附加质量和阻尼系数的渐进特性。文献［14］考虑具有修正PM波谱的长峰不规则浪，基于海浪幅值响应算子（RAO）研究了船舶在海浪中的六自由度运动预报模型。为了有效地量化海洋环境对动力定位船舶的作用，文献［15］提出了海洋环境负载（包括风、海浪和海流）的建模方法，并运用MATLAB的M文件和SIMULINK分别编制了风干扰力和力矩计算及随机海浪的仿真程序。在三级海况下，实现了对海洋环境的仿真，得到了合理的仿真结果。文献［16］考虑到船舶的动态特性存在固有的强非线性以及非线性控制改善系统性能和鲁棒性的能力，将非线性控制理论应用到船舶动力定位控制系统的设计中，对某供应船的计算机模型进行仿真，验证了非线性控制系统是有效的。文献［17］提出并验证了基于线性核函数在线支持向量回归的模型预测控制方案。在线支持向量回归算法的引入可以通过在线调整，确保预测模型的精确性。

2.2 船舶数学模型参数辨识

文献［18］讨论了使用两个并行测量序列来估计动力定位船舶模型参数的离线并行扩展卡尔曼滤波器算法（Off-line Parallel Extended Kalman Filter（EKF）Algorithm），见表1。最后采用一项以供给船为对象的全尺度的海上试验来验证提出的参数估计器的收敛性和鲁棒性。

实验对象以挪威ABB公司的“Far Scandia”号供给船为原型。该船总长76.2m，船宽18.8m，型深8.25m，吃水6.25m，净吨位4 200 t，主发动机功率3 533 kW。推进器配置：左右舷两个主推进器u1、u2，尾部隧道式侧推u3、u4，艏部隧道式侧推u5，艏部方位角式推进器u6。质量阵M″可利用文献［19］里介绍的Strip Theory计算得到：

表1 离散时间摘要扩展卡尔曼滤波

为了得到需要辨识的量，需重复进行3项（每项2次，共6次）海上试验，以此提高参数估计器的收敛性和表现。具体如下：

第1项：解耦了的纵荡运动。船舶仅依靠主螺旋桨u1和u2实现恒速前进，艏向通过艏侧推控制。第2项：结耦了的横荡与艏摇运动。通过三个隧道式推进器u3、u4、u5实现两次结耦了的横荡与艏摇运动。第3项：在结耦的横荡与艏摇运动中得到方位角式推进器u6的推力系数K6。

第1项是为了计算主螺旋桨的推力系数K1和Xu，需要的输入量是Xu˙。本文中Xu˙的计算方法是利用文献［19］里介绍的切片法。第2项是为了计算结耦了的横荡与艏摇运动的参数数值，可以辨识出的向量为第3项是为了计算全方位推进器的推力系数K6。

使用动量方程来代替标准动力学方程，不仅可以显著提高状态和参数估计器的性能，还具有以下优点：

（1）增加数据冗余度；

（2）降低量测噪声；

（3）降低环境干扰；

（4）增加数据记录长度；

（5）以对参数分批进行辨识等手段提高参数辨识的精确度。

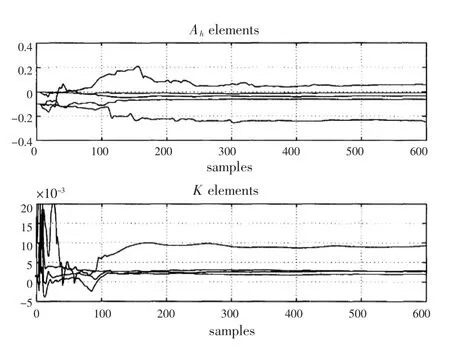
图2 实验辨识得到的参数曲线

经实验辨识出的动量方程中的量：

写成动力定位模式下的状态空间表达式为：

3 环境扰动数学模型

3.1 风扰动数学模型

风的作用可分为平缓变化的风和快速变化的风。将风速分量定义为：

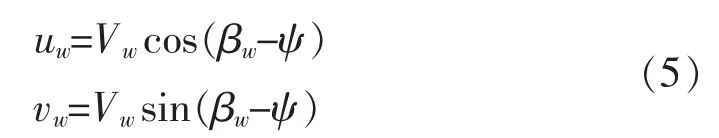
式中，uw和vw分别为风速在X轴和Y轴的分量；Vw和βw分别表示风速和风向。如图1所示。假设风速远大于船速，风在纵荡、横荡和艏摇方向的负荷向量可表述为［5］：

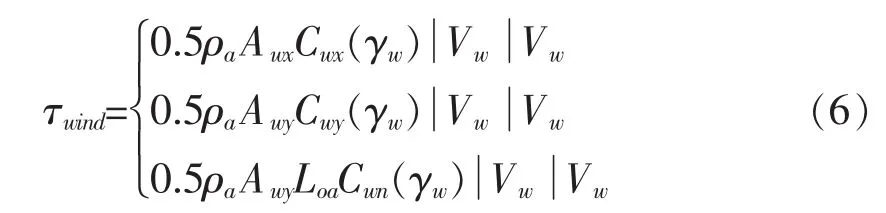
式中，风的相对角为γw=βw-ψ；ρa为空气密度，单位为kg/m3；Loa为船舶总长，单位为m；Vw为相对风速，单位为kn；Awx和Awy为正投影面积和侧投影面积，单位均为m2；Cwx（γw）、Cwy（γw）和Cwn（γw）分别为纵荡、横荡和艏摇方向的无因次风系数，是通过Isherwood半经验公式得到的。

3.2 波浪扰动数学模型

波浪干扰力一般分为两种：一种是一阶波浪干扰力，也称高频波浪干扰力。这是在假设波浪为微幅波，未引起船舶大幅摇荡的情况下，认为船舶受到与波高成线性关系并且与波浪同频率的波浪力。另一种是二阶波浪力，也称波浪漂移力，该波浪力与波高平方成比例。

这种具有高频率小振幅振荡特性的波浪所产生的一阶波浪干扰力最主要是引发船舶的纵摇和垂荡运动，对横摇的影响稍次之，而对横荡及艏摇运动的影响相对来说就小一些。至于具有慢时变特性的二阶波浪干扰力，本身同时又是非线性的，它仍然和波浪的频率有关。波浪的二阶漂移力不但会改变船舶航行的航向和航迹，尤其对于在锚泊状态下船舶位置的移动及钻井平台的动力定位系统的工作等均有重要影响。

下面介绍一种估算二阶波浪漂移力方法。1974年，Newman提出一种应用频域波浪漂移力系数的估算方法。通过把波谱（通常选用P-M谱）分为N等份，每份有相对应的波浪频率wj和波幅A。这样波浪漂移力对横荡、纵荡、艏摇运动的作用力计算公式为［5］：

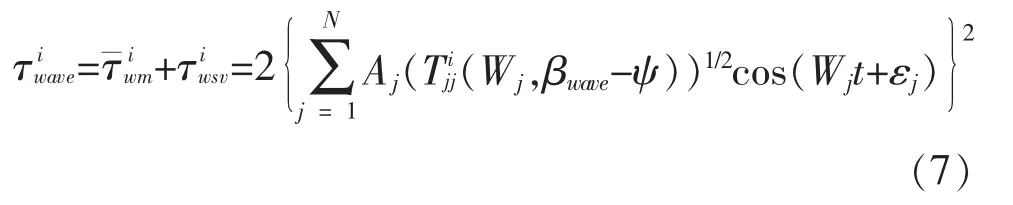
可以通过对本估算式进行改变，以避免在数值上产生无物理意义的高频分量。还可对本式进行扩展，用来包括波浪蔓延（wave spreading）。

3.3 海流扰动数学模型

作用在海上动力定位船舶上的海流具有方向和速度的特征，研究中一般不考虑在大地坐标系下铅垂方向运动。海流分为恒定流和潮汐流。恒定流一般为固定方向和速度的海流，如洋流。潮汐流指海洋因为潮汐运动而引起的海水流动，其典型的表现为海流方向的缓慢变化。但对于动力定位来说，海流的大小与方向可以认为是确定的，所以海流的模型可以统一按照大小和方向恒定来确立。流的速度分量表示为［5］：

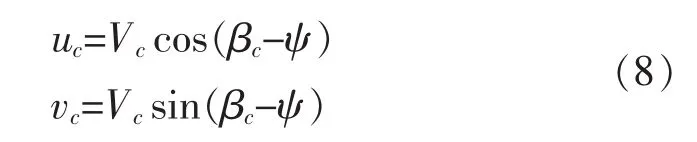
式中：uc和vc分别为流速在X轴和Y轴的分量；Vc和βc分别代表流速和流向。如图1所示。

在此没有考虑艏摇方向的流速，而海流对水面船舶的作用可以通过将各海流速度分量引入到船的运动方程中由相对速度向量vr=［u-uc，v-vc，r］T体现。

4 结论

本文讨论了船舶及推进器动力学数学模型与船舶外界环境干扰因素数学模型的建模策略。通过对已有研究方法的分析研究与总结，有助于建立适用于各种海况和操作模式的船舶动力定位系统非线性数学模型。

［1］杜佳璐，张显库，汪思源，等.船舶动力定位系统的自适应非线性控制器设计［C］//Proceedings of the 29thChinese Control Conference.Beijing，2010：585-589.

［2］周利，王磊，陈恒.动力定位控制系统研究［J］.船海工程，2008，37（2）：86-91.

［3］马超，庄亚锋，陈俊英.船舶动力定位系统技术［J］.中国造船，2009，50（增刊）：52-57.

［4］贾欣乐，杨盐生.船舶运动数学模型机理建模与数学建模［M］.大连：大连海事大学出版社，1999：294-356.

［5］Fossen T I.Handbook of Marine Craft Hydrodynamics and Motion Control［M］.Wiley&Sons Ltd.，2011：81-83.

［6］Balchen JG，Jenssen N A，Sælid S.Dynamic Positioning Using Kalman Filtering and Optimal Control Theory［C］//Proceedings of IFAC/IFIP Symposium on Automation in Offshore Oil Field Operation.Norway，1976:183-186.

［7］Balchen J G，Jenssen N A.Mathisen E，et al.Dynamic Positioning System Based on Kalman Filtering and Optimal Control［J］.Modeling，Identification and Control.1980，1（3）：135-163.

［8］Strand JP，Fossen T I.Nonlinear Passive Observer Design for Shipswith AdaptiveWave Filtering，In：New Directions in Nonlinear Observer Design（Nijmeijer H.，Fossen T.I.）［M］.London：Springer-Verlag London Ltd.，1999：113-134.

［9］Guttorm T，Jérôme J，Fossen T I.Nonlinear Dynamic Positioning of Shipswith Gain-Scheduled Wave Filtering［C］//The Proceedings of 43rd IEEE Conference on Decision and Control，Atlantis，Paradise Island，Bahamas，December 2004：5340-5347.

［10］Do K D.Global Robust and Adaptive Output Feedback Dynamic Positioning of Surface Ships［C］//The Proceedings of 2007 IEEE International Conference on Robotics and Automation.Roma，April 2007：10-14.

［11］王晓声.船舶动力定位系统设计及试验研究［J］.中国造船，1991（3）：12-21.

［12］边信黔，严浙平，施小成.船舶动力定位系统参数辨识方法的研究［J］.船舶工程，1999（1）：36-38.

［13］姜哲，石珣，王磊.动力定位船舶水动力参数数值试验研究［J］.实验室研究与探索，2005（12）：14-17.

［14］李文魁，张博，田蔚风，等.一种波浪中的船舶动力定位运动建模方法研究［J］.仪器仪表学报，2007（6）：1051-1054.

［15］施小成，王元慧.船舶动力定位海洋环境的建模与仿真［J］.计算机仿真，2006（11）：237-239.

［16］刘芙蓉，陈辉.基于非线性控制理论的船舶动力定位控制系统的数学模型［J］.船海工程，2009（5）：92-95.

［17］邓志良，胡寿松，张军峰.船舶动力定位系统的在线模型预测控制［J］.中国造船，2009（6）：87-96.

［18］Fossen T I.Identification of Dynamically Positioned Ships［J］.Control Engineering Practice，Volume 4，Issue 3，March 1996：369-376.

［19］Faltinsen OM.Sea Loadson Shipsand Offshore Structures［M］.Cambridge University Press，1990：41-45.

Identification methods for mathematic model of ship dynamic positioning systems

LI Wen-hua1DU Jia-lu2ZHANG Yin-dong1SONG Jian1SUN Yu-qing1CHEN Hai-quan1
（1.College of Marine Engineering，Dalian Maritime University，Dalian 116026，China；2.College of Information Science and Technology，Dalian Maritime University，Dalian 116026，China）

Ship dynamic positioning system is one of the key technologies to exploit the deep-sea resources.Mathematic model for ship dynamic positioning system with higher quality is demanded as the offshore oil and gas industry goes to deep-sea.At first，the significance of the dynamic positioning system and its mathematic model are introduced.Then，the identification and construction procedure of the ship and thruster mathematic model are established in detail.At last，strategies for the modeling of ship environmental disturbances are briefly discussed.

ship；dynamic positioning system；mathematicmodel；identification；environmental disturbance

U661.33

A

1001-9855（2012）03-0055-05

国家自然科学基金资助项目（51079013，51109021）；辽宁省教育厅高等学校科研资助项目（LT2010013）；2012年交通运输部应用基础研究项目资助；中央高校基本科研业务费专项资金资助项目（2011QN109）。

2011-12-02；

2011-12-13

李文华（1980-），男，汉族，博士，讲师，主要从事船舶动力定位系统建模与控制的研究。